
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резервування грошових засобів на покриття випадкових затратСодержание книги
Поиск на нашем сайте Створення резерву грошових засобів на покриття випадкових затрат — це один із способів зниження ризику, який передбачає встановлення співвідношення між потенційним ризиком і величиною затрат, необхідних для подолання збоїв у виконанні зобов’язань (проекту). Для визначення обсягів грошей на покриття випадкових затрат (збитків), переоцінки їх в процесі роботи над проектом і уточненням суми резерву на основі фактичних даних можуть бути використані всі викладені у попередньому матеріалі методи якісного і кількісного аналізу ризику. Визначення структури резерву на покриття імовірних непередбачуваних затрат проводиться за допомогою одного з двох можливих способів. Згідно з першим способом (рис. 2.1.13) резерв ділять на дві частини: на загальний і спеціальний. Загальний резерв повинен покривати зміни в кошторисі, добавки до загального обсягу грошей по контракту та інші елементи.
Рис. 2.1.13. Резерви, узгоджені в контракті на покриття ймовірних затрат (збитків) Спеціальний резерв складається з надбавки на покриття зростання цін, зростання затрат по окремих позиціях, а також на сплату позовів по контрактах. Згідно з другим способом (рис. 2.1.14) структура резервів передбачає визначення імовірних затрат (збитків) по видах затрат, наприклад на заробітну плату, матеріали, субконтракти.
Рис. 2.1.14. Визначення структури резервів на покриття ймовірних збитків (затрат) Моделі оптимізації ступеня ризику та деякі стратегії формування запасів Різновиди задач управління запасами та їх складність зумовили створення великої кількості математичних моделей, ефективне використання яких неможливе без застосування економіко-математичних методів та ЕОМ. Найістотнішим чинником, який необхідно враховувати при розробці моделей управління запасами, є час. Статичні моделі управління запасами лише наближено відповідають реальним умовам. Більш точний розв’язок може бути одержаний на базі використання динамічних моделей. Окрім того, в переважній більшості реальних задач попит є випадковою величиною, розподіл імовірності якої може бути як відомим, так і невідомим. Внаслідок цього виникає економічний ризик, зумовлений невизначеністю, стохастичністю щодо величини попиту. Величина ризику може бути визначена як відхилення потреб у запасах від середньої (сподіваної) величини. Модель М. Міллера і Д. Орра Утримання певного обсягу грошових засобів на банківському рахунку або ж у формі готівки в касі компанії (фірми) є важливим для нормального її функціонування. Грошові засоби потрібні компаніям для регулювання різного роду зобов’язань. Утримання ж надмірного обсягу грошових засобів може бути чинником, що знижує загальну ефективність господарювання компанії (підприємства). Оптимізація величини грошових засобів реалізується за допомогою різних методів. Розглянемо, зокрема, модель М. Міллера і Д. Орра. Ця модель має імовірнісний характер — потоки чистих доходів і видатків трактуються як випадкові змінні величини, закон розподілу яких може бути описаний двома параметрами: математичним сподіванням (середньою величиною) та дисперсією (варіацією). Приймається також гіпотеза, що функція розподілу потоку чистих грошових надходжень і видатків має нормальний закон розподілу. Головними у моделі є три величини: оптимальна величина сальдо грошових засобів х *, їх максимальний рівень х max і мінімальний рівень x min. Причому мінімальний рівень x mіn задають менеджери підприємства, а решту величин х *і x max визначають за допомогою моделі. Наведемо лише остаточні результати, опускаючи виведення відповідних формул. При заданому рівні величини x mіn, значення х *та x max можна обчислити за формулами:
та
де Кs — стала величина обсягу однієї угоди щодо продажу цінних паперів чи отримання позики; km — величина втрачених можливостей, пов’язана з утриманням сальдо грошових засобів (дорівнює нормі відсотку, яку можна було б отримати, купивши цінні папери); s — середньоквадратичне відхилення потоку чистих грошових надходжень. Модель формування оптимального резерву Задача управління запасами в умовах невизначеності та зумовленого нею ризику вимагає визначення оптимального резерву. Одним з простих способів, що дає змогу вирішити проблему резерву, є застосування принципу гарантованого результату, тобто обрання досить великого резерву, який гарантує мінімальний ризик. Це може призвести до так званого ризику невикористаних можливостей — великі резерви пов’язані з відволіканням значних коштів. Тому вводяться додаткові гіпотези. Зокрема, в основу розрахунку необхідного резерву закладається поняття допустимого ризику — ймовірності того, що потреба в запасах не перевищить наявного резерву. Вводиться поняття коефіцієнта ризику pz, який виражає імовірність того, що потреби у запасах виявляться незабезпеченими через недостатність резерву. Значення коефіцієнта ризику pz вибирається не більшим від певної фіксованої величини a — порогу дозволеності. Позначимо через V потребу в продукції між двома поставками, через m — розмір постачання (розмір партії). Сформулюємо задачу. Необхідно визначити такий обсяг резерву К, щоб коефіцієнт ризику pz, тобто ймовірність того, що резерв виявиться недостатнім (іншими словами, — ймовірність появи дефіциту), був би не більшим від заданого значення порогу дозволеності, тобто:
Для визначення величини К потрібно знати закон розподілу випадкової величини V. Припустимо, зокрема, що потреба в запасах, тобто величина V, розподілена за нормальним законом розподілу з параметрами m та s, де m — сподіване значення, s — середньоквадратичне відхилення. Поклавши
де
де А тому отримуємо, що резерв, який відповідає коефіцієнту ризику Можна зробити висновок, що розміри резерву К визначаються прийнятим коефіцієнтом ризику та коливанням (розкидом) потреб у запасах, що характеризуються середньоквадратичним відхиленням s. Величину s можна наближено визначити на базі статистичної обробки значень попиту у попередні періоди. Вище наведено один з простих методів урахування ризику. Однією з проблем, що ускладнює задачу, є проблема обрання конкретного раціонального значення коефіцієнта ризику. Тут ефективно можуть застосовуватися, зокрема, експертні процедури та теорія корисності, що дає змогу відобразити й врахувати відношення суб’єктів прийняття рішень до ризику тощо.
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |



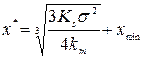 ,
, ,
,
 .
. (тобто здійснивши нормування випадкової величини V),
(тобто здійснивши нормування випадкової величини V),  і враховуючи, що функція щільності розподілу ймовірності випадкової величини U — це функція Гауса, отримуємо:
і враховуючи, що функція щільності розподілу ймовірності випадкової величини U — це функція Гауса, отримуємо: ,
, — функція Лапласа. Отже:
— функція Лапласа. Отже: ,
, — функція, обернена до
— функція, обернена до  , повинен дорівнювати щонайменше
, повинен дорівнювати щонайменше  .
.


