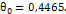Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерій Колмогорова при складній гіпотезіСодержание книги
Поиск на нашем сайте а) Оцінку скалярного або векторного параметра розподілу F (x, θ) можна обчислювати методом максимальної правдоподібності на підставі формули б) Значення статистики Колмогорова SK або її мінімума розраховують по формулі Sk = в) Розподіл G(SK½H0) вибирають з таблиці А.7. Критичні значення критерію Sα при заданому α можуть бути взяті з таблиці А.8. д) Гіпотезу про узгодженість не відкидають, якщо P {S > S*K} = 1 - G (SK ½ H0) > α (або S*K < Sα) Критерій Смирнова при складній гіпотезі Особливості застосування критерію типу Смирнова наступні. а) Оцінку скалярного або векторного параметра розподілу F (x, θ) обчислюють методом максимальної правдоподібності б) Значення статистики Смирнова Sm обчислюють за формулою Sm = в) Розподіл G(Sm½H0) вибирають з таблиці А.11. Критичні значення критерію Sα при заданому α можуть бути взяті з таблиці А.12. г) Гіпотезу про згоду не відкидають, P {S > S*m} = 1 - G (Sm ½ H0) > α (або S*m < Sα). Вплив обсягу вибірки на розподіл при складних і простих гіпотезах У разі перевірки простих гіпотез граничними розподілами статистик критеріїв Колмогорова і Смирнова можна користуватися при n > 20. Дослідження методами статистичного моделювання залежності розподілів статистик всіх розглянутих тут непараметричних критеріїв від обсягу вибірки при перевірці різних як простих, так і складних гіпотез показує, що це справедливо у всіх випадках. Наприклад, малюнок 1 іллюструє, як при збільшенні обсягу вибірки (n = 5, 10, 20) міняється розподіл G (Sn ½ H 0) статистики Колмогорова Sk в разі перевірки простої гіпотези про приналежність вибірки нормальному закону. На цьому малюнку відображено також граничний розподіл статистики - функція розподілу Колмогорова K(S). Емпіричні розподіли G (Sn ½ H 0) при великих n практично зливаються з K(S), і на малюнку вони не показані. Як видно, при малих n розподіл істотно відрізняється від граничного, але вже при n ≥ 15 - 20 помилка при обчисленні ймовірності узгодження P {S > S*} виявляється досить малою.
Малюнок 1 - Залежність від n розподілів G (Sn ½ H 0) статистики SK Колмогорова при простій гіпотезі (H0 - нормальний розподіл): n = 5, 10, 20. K(S) - функція граничного розподілу Колмогорова
Та ж сама картина спостерігається у випадку перевірки складних гіпотез про згоду. На малюнку 2, при n = 5, 10, 20, 1000 представлені розподіли G (Sn ½ H 0) статистики SK в разі перевірки аналогічною, але вже складною, гіпотезою про нормальність.
Малюнок 2 - Залежність від n розподілів G (Sn ½ H 0) статистики SK Колмогорова при складній гіпотезі; n = 5, 10, 20, 1000
Малюнок 3 - Залежність від n розподілів G (Sn ½ H 1) статистики Sm Смирнова при складній гіпотезі (H0 - нормальний розподіл; H1 - логістичний); n = 20, 100, 500, 1000
Малюнок 4 - Функції розподілу нормального і логістичного законів
При малих n найбільші відхилення від граничних розподілів спостерігаються на «хвостах». І при простих, і при складних гіпотезах із зростанням n розподілу G (Sn ½ H 0) рівномірно сходяться до граничного. Але якщо у випадку простих гіпотез із зростанням n збільшується ймовірність великих значень статистик, то у випадку складних зростають ймовірності і великих, і малих значень статистик. Таким чином, розподілу G (Sn ½ H 0) статистик непараметричних критеріїв при простих та складних гіпотезах із зростанням n дуже швидко сходяться до граничних, і вже при n ≥ 15 - 20 можна, не побоюючись великих помилок, користуватися цими граничними законами при аналізі даних. Для надійного розрізнення близьких законів розподілу, зокрема за допомогою критерію згоди Колмогорова, може знадобитися вибірка досить великого обсягу. Приклади 1. Перевірити гіпотезу про однорідність двох вибірок.
Розв’язок: Так як вибірка є незгрупованою, то для перевірки гіпотези однорідності вибірок X і Y можна скористатися критерієм однорідності Смирнова. Задамо рівень значущості Статистика критерію однорідності Смирнова:
2. Перевірити просту гіпотезу про приналежність вибірки експоненціальному закону. Впорядкована вибірка обсягом 100 спостережень має вигляд:
Розв’язок: Перевіряюча гіпотеза має вигляд Н0 : А) Критерій Колмогорова. Значення статистики розраховують за формулою Sk = Б) Критерій Смирнова. Значення статистики розраховують за формулою Sm = Як бачимо, при заданні рівня значущості α <0,2548 (для критерію Смирнова), немає підстав для відхилення перевіряючої гіпотези за критеріями згоди.
3. Перевірити складну гіпотезу про приналежність вибірки з прикладу 2 експоненціальному закону Перевіряюча гіпотеза має вигляд Н0 : А) Критерій Колмогорова. Значення статистики розраховують за формулою Sk = Б) Критерій Смирнова. Значення статистики розраховують за формулою Sm = По критеріям згоди вибірки з експонентним законом досить задовільні.
Висновок В даній курсовій роботі мною було розглянуто один з непараметричних критеріїв,оснований на аналізі емпіричного розподілу і функції розподілу в генеральній сукупності, а саме критерій Колмогорова-Смирнова,який застосовується в математичній статистиці з метою перевірки простих і складних гіпотез. Було розглянуто відмінність окремо критерію Колмогорова та окремо критерію Смирнова. На основі теоретичної частини я розглянула декілька практичних моментів з застосуванням приведених вище алгоритмів кожного з параметрів.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
.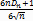 на підставі формул Dn = max(
на підставі формул Dn = max( ), при
), при  та
та  .
.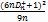 на підставі формул
на підставі формул 



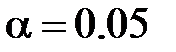 .
. , де
, де 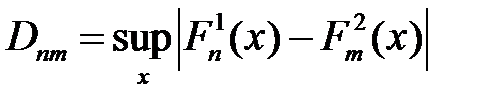 підпорядковується розподілу Колмогорова
підпорядковується розподілу Колмогорова 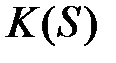 .
. 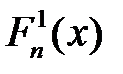 – емпірична функція розподілу по першій вибірці,
– емпірична функція розподілу по першій вибірці, 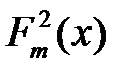 – по другій. Проводячи обчислення, отримуєм:
– по другій. Проводячи обчислення, отримуєм:  ,
,  ,
, 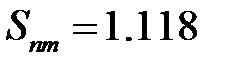 . Знаходимо за табличкою критичне значення статистики Смирнова при
. Знаходимо за табличкою критичне значення статистики Смирнова при 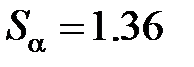 . Оскільки
. Оскільки  , то нема підстав для відхилення гипотези про однородності вибірок X и Y.
, то нема підстав для відхилення гипотези про однородності вибірок X и Y. 0.1
0.1
 при
при 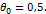

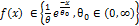 при
при