
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка гіпотез про узгодженністьСодержание книги
Поиск на нашем сайте
Застосовуючи критерії узгодженості для перевірки відповідності спостережуваного відомого розподілу теоретичному закону, слід розрізняти перевірку простих і складних гіпотез. Проста перевіряюча гіпотеза має вигляд H0: F (x) = F (x, θ), де F (x, θ) - функція розподілу ймовірностей, з якої перевіряють узгодженість спостережуваної вибірки, а θ - відоме значення параметра (скалярного або векторного). Складна перевіряюча гіпотеза має вигляд H0: F (x) Î {F (x, θ), θ Î У процесі перевірки узгодженості по вибірці обчислюють значення S* статистики використовуваного критерію. Потім для того, щоб зробити висновок про прийняття або відхилення гіпотези Н0, необхідно знати умовний розподіл G (S ½ Н0) статистики S при справедливості Н0. У процесі перевірки узгодженості по вибірці обчислюють значення S* статистики використовуваного критерію. Потім для того, щоб зробити висновок про прийняття або відхилення гіпотези Н0, необхідно знати умовний розподіл G (S ½ Н0) статистики S при справедливості Н0. І якщо ймовірність P досить велика, принаймні P {S Перевірка простої гіпотези При перевірці узгодженосі відомого розподілу з теоретичним розподілом випадкової величини Х діють наступним чином. а) Формулюють перевіряючу гіпотезу, вибираючи теоретичний розподіл випадкової величини, узгодженність якого з досвідченим розподілом цієї величини слід перевірити; б) Із сукупності відбирають випадкову вибірку обсягу n. Отримані результати спостережень розташовують у порядку їх зростання, так, що у розпорядженні мають впорядковану вибірку значень x1 ≤ х2 ≤... ≤ хn ; в) У відповідності з обраним критерієм перевірки обчислюють значення статистики S* критерію (за формулою Sk = г) У відповідності з обраним критерієм перевірки обчислюють значення P де G (s ½ H 0) - розподіл статистики критерію при справедливості гіпотези H0. Якщо P {S> S*} > α, де α - рівень значимості, то немає підстав для відхилення перевіряючої гіпотези. В іншому випадку перевіряючу гіпотезу Н0 відкидають. Можна обчислюване значення статистики S* порівняти з критичним значенням Критерій Колмогорова при простій гіпотезі Порядок перевірки простої гіпотези про узгодженість відомого розподілу з теоретичним - відповідно до пункту 4 перерахування підпунктів а) - г). У разі обраного критерію Колмогорова: а) Значення статистики Колмогорова Sк обчислюють за формулою Sk = б) Значення ймовірності P {S> S*к} = 1 - K(S*к) обчислюють за функцією розподілу Колмогорова K(S) = в) Критичні значення критерію Критерій Смирнова при простій гіпотезі Порядок перевірки простої гіпотези про узгодженість відомого розподілу з теоретичним - відповідно до пункту 4 перерахування підпунктів а) - г). У разі обраного критерію Смирнова: а) Значення статистики Смирнова Sm обчислюють за формулою Sm = б) Значення ймовірності P {Sm > S*m} = в) Гіпотезу H0 не відкидають, якщо для обчисленого за вибіркою значення статистики S*m P {Sm > S*m} = Перевірка складної гіпотези При перевірці узгодженості відомого розподілу з теоретичним розподілом випадкової величини X діють наступним чином. а) Формулюють перевіряючу гіпотезу, вибираючи теоретичний розподіл F(х, θ) випадкової величини, узгодженість якого з відомим розподілом цієї величини слід перевірити. б) Із сукупності відбирають випадкову вибірку обсягу n. Отримані результати спостережень розташовують у порядку їх зростання, так, що у розпорядженні мають впорядковану вибірку значень в) У відповідності з обраним критерієм перевірки, теоретичним розподілом F (x, θ) визначають розподіл статистики критерію G (S ½ H0) при справедливості гіпотези H0. г) Обчислюють значення P ж) Якщо P{S > S*} > α, де α - рівень значимості, то немає підстав для відхилення перевіряючої гіпотези. В іншому випадку перевіряюча гіпотеза H0 відкидається. Можна обчислене значення статистики S* порівняти з критичним значенням Sα, обумовленим з умови
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.59.107 (0.008 с.) |

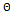 }, де
}, де  - область визначення параметра θ. У цьому випадку оцінку параметра розподілу обчислюють за тією ж самою вибіркою, за якою перевіряють згоду. Якщо оцінку обчислюють за іншою вибіркою, то гіпотеза проста.
- область визначення параметра θ. У цьому випадку оцінку параметра розподілу обчислюють за тією ж самою вибіркою, за якою перевіряють згоду. Якщо оцінку обчислюють за іншою вибіркою, то гіпотеза проста.
 S*}
S*}  (s ½ Н0) - умовна щільність, а α - рівень значущості (ймовірність помилки 1-го роду - відхилити справедливу гіпотезу Н0), то прийнято вважати, що немає підстав для відхилення гіпотези Н0.
(s ½ Н0) - умовна щільність, а α - рівень значущості (ймовірність помилки 1-го роду - відхилити справедливу гіпотезу Н0), то прийнято вважати, що немає підстав для відхилення гіпотези Н0.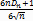 );
); ,
, , що визначається з умови
, що визначається з умови  . Гіпотезу про узгодженість відкидають, якщо значення статистики потрапляє в критичну область, тобто при S* >
. Гіпотезу про узгодженість відкидають, якщо значення статистики потрапляє в критичну область, тобто при S* >  .
. ), при
), при  та
та  .
. або беруть з таблиці А.1.
або беруть з таблиці А.1.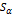 при заданому
при заданому  можуть бути взяті з табліці А.2.
можуть бути взяті з табліці А.2.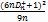 на підставі формул
на підставі формул  обчислюють за функцією
обчислюють за функцією  - розподілу (з двома ступенями вільності).
- розподілу (з двома ступенями вільності). .
.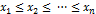 .
.
 .
. . Гіпотезу про узгодженість не відкидають, якщо S* < Sα.
. Гіпотезу про узгодженість не відкидають, якщо S* < Sα.


