
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Ома для замкнутой цепиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для замкнутой электрической цепи (рис. 2.5) ЭДС источника, согласно (1.3), можно определить выражением
где R0 - сопротивление источника; R - сопротивление потребителя (сопротивлением проводов пренебрегают).
Из (1.10) следует, что ток в замкнутой цепи равен
Из (1.10) можно определить напряжение на внешнем участке цепи, т. е. напряжение на клеммах источника U между точками А и В (см. рис. 2.5).
Таким образом, напряжение U на клеммах источника электрической энергии меньше, чем ЭДС этого источника (Е) на величину падения напряжения U0 на внутреннем сопротивлении источника. Отсутствие нагрузки - ключ К разомкнут - соответствует режиму холостого хода. При этом IR0 = 0. Вольтметр (V), подключенный к клеммам источника А и В (рис. 2.5), при отсутствии нагрузки (I = 0) показывает ЭДС источника Е
Если же ключ К замкнут (I ≠ 0), то вольтметр покажет напряжение U на клеммах источника, которое меньше ЭДС на величину Из (1.12) следует, что с увеличением нагрузки, т. е. с увеличением тока I, напряжение на клеммах источника уменьшается, что можно показать графически на внешней характеристике источника (рис. 2.6).
Очевидно, чем больше внутреннее сопротивление источника R0, тем меньше будет напряжение на его клеммах при нагрузке I|.
Энергия и мощность электрического тока В замкнутой электрической цепи источник затрачивает электрическую энергию WИСТ на перемещение единицы положительного заряда по всей замкнутой цепи, т. е. на внутреннем и внешнем участках ((1.3) и рис. 2.3).
ЭДС источника определяется выражением
так как Энергия источника расходуется на потребителе (полезная энергия)
и на внутреннем сопротивлении источника (потери)
Потерей энергии в проводах, при незначительной их длине, можно пренебречь. Из закона сохранения энергии следует
Во всех элементах электрической цепи происходит преобразование энергии (в источниках различные виды энергии преобразуются в электрическую, в потребителях - электрическая в другие виды энергии). Скорость такого преобразования энергии определяет электрическую мощность элементов электрической цепи
Обозначается электрическая мощность буквой Р, а единицей электрической мощности является ватт, другими словами, [ Р ] = Вт (ватт)
Таким образом, мощность источника электрической энергии определяется выражением
Мощность потребителя, т. е. полезная, потребляемая мощность, будет равна
Если воспользоваться законом Ома для участка электрической цепи, то полезную мощность можно определить следующим выражением:
Потери мощности на внутреннем сопротивлении источника
Для любой замкнутой цепи должен сохраняться баланс мощностей
Так как электрическая мощность измеряется в ваттах, то единицей измерения электрической энергии является [ W ] = [ P·t ] = Вт·с. Коэффициент полезного действия электрической цепи η определяется отношением полезной мощности (мощности потребителя) ко всей затраченной мощности (мощности источника)
Закон джоуля – Ленца В проводах линии передачи электрической энергии, обмоток якорей и полюсов электрических машин, электробытовых приборов и других потребителей происходит преобразование электрической энергии в тепловую. Ток I, протекая по проводнику с сопротивлением R, нагревает этот проводник. За время t в этом проводнике выделяется тепло, количество которого определяется количеством электрической энергии, затраченной в этом проводнике, т. е.
где Q - количество тепла, выделенного в проводнике, Вт·с. Приведенная зависимость (1.24) является математическим выражением закона Джоуля - Ленца. Таким образом, закон Джоуля - Ленца устанавливает зависимость между количеством тепла и электрической энергией: количество тепла, выделенное током в проводнике, пропорционально квадрату тока, сопротивлению проводника и времени прохождения тока по проводнику. Количество тепла Q измеряется иногда внесистемной единицей - калорией (количество тепла, необходимое для нагревания 1 г воды на 1 °С), Причем 1 кал = 4,187 Дж, следовательно, 1 Вт*с = 1 Дж = 0,24 кал. Для определения количества тепла Q в калориях пользуются выражением
Коэффициент 0,24 называют электротермическим эквивалентом, который устанавливает зависимость между электрической и тепловой энергией. Преобразование электрической энергии в тепловую широко используется в разнообразных электронагревательных приборах. Однако преобразование электрической энергии в тепловую вызывает и непроизводительные расходы энергии в электрических машинах, трансформаторах и других элементах электрической цепи снижает их КПД.
Законы Кирхгофа В схемах электрических цепей можно выделить характерные элементы: ветвь, узел, контур. Ветвью электрической цепи называется ее участок, на всем протяжении которого величина тока имеет одинаковое значение. Узлом электрической цепи (узловой точкой) называется место соединения электрических ветвей. В узловой точке сходятся как минимум три ветви (проводника). Контуром электрической цепи называют замкнутое соединение, в которое могут входить несколько ветвей (рис. 3.4б). Ветви, содержащие источник электрической энергии, называются активными, а ветви, не содержащие источников, называются пассивными. Первый закон Кирхгофа. В разветвленной цепи ток в различных ветвях может иметь различное значение. Сумма токов, входящих в узловую точку разветвленной цепи, должна быть равна сумме токов, выходящих из этой точки. На рис. 3.4а показана узловая точка цепи А, для которой можно записать
Выражение (1.26) представляет собой математическую запись первого закона (правила) Кирхгофа. Первый закон Кирхгофа формулируется так: алгебраическая сумма токов в ветвях, соединенных в один узел, равна нулю. Токи, входящие в узел, принято считать положительными, а выходящие из узла - отрицательными.
Второй закон Кирхгофа устанавливает зависимость между ЭДС и падением напряжения в замкнутом контуре любой электрической цепи. Точки А, В, С и D являются узловыми точками (рис. 3.4б), поскольку в каждой из них сходятся четыре проводника. Определим потенциал каждой узловой точки
Сумма потенциалов всех узловых точек замкнутого контура равна
Сократив все потенциалы замкнутого контура, слева и справа от знака равенства, и перенеси все ЭДС замкнутого контура налево от знака равенства, а падения напряжения оставив справа, можно записать
что и является вторым законом Кирхгофа, который формулируется так: Алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи
Напряжение представляет собой математическую запись второго закона (правила) Кирхгофа. Для определения знаков в алгебраической сумме направление контура выбирается произвольно: по часовой или против часовой стрелки. ЭДС источника, совпадающая с выбранным направлением обхода контура, считается положительной, а не совпадающая - отрицательной. Падение напряжения на сопротивлении R считается положительным, если ток, протекающий через него, совпадает с выбранным направлением обхода контура, или отрицательным - если не совпадает. Для электрической цепи, изображенной на рис. 3.4б, второй закон Кирхгофа записывается так:
Направление обхода контура в приведенном расчете выбрано по часовой стрелке.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.124 (0.007 с.) |

 (1.10)
(1.10)
 (1.11)
(1.11) (1.12)
(1.12)
 , равную падению напряжения на внутреннем сопротивлении источника (1.12).
, равную падению напряжения на внутреннем сопротивлении источника (1.12).

 . Из этого выражения следует, что энергия, затраченная источником, равна
. Из этого выражения следует, что энергия, затраченная источником, равна (1.13)
(1.13) , что вытекает из определения величины тока
, что вытекает из определения величины тока  .
. (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17)
 (1.18)
(1.18) (1.19)
(1.19)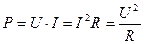 (1.20)
(1.20) (1.21)
(1.21) (1.22)
(1.22) (1.23)
(1.23) (1.24)
(1.24) (кал) (1.25)
(кал) (1.25) или
или 
 (1.26)
(1.26)
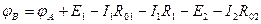 (обход по току);
(обход по току); (обход по току);
(обход по току); (обход против тока);
(обход против тока); (обход против тока).
(обход против тока).

 (1.27)
(1.27)



