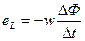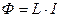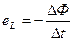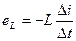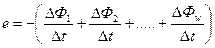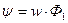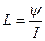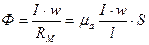Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величина и направление индуктированной ЭДССодержание книги
Поиск на нашем сайте
Индуктированная ЭДС. возникает в следующих трех случаях: - когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого; - когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем э. д. с. (взаимоиндукция); - когда изменяющееся магнитное поле какого-либо проводника индуктирует в нем самом э. д. с. (самоиндукция). Таким образом, всякое изменение во времени величины магнитного потока
где ΔФ - магнитный поток, пересеченный проводником за промежуток времени Δt. Величина индуктированной э. д. с. в проводнике зависит: - от величины индукции В магнитного поля, так как чем плотнее расположены магнитные линии, тем большее число их пересечет проводник за единицу времени (секунду); - от скорости движения проводника V в магнитном поле, так как при большей скорости движения проводник может больше пересечь магнитных линий в секунду; - от активной (находящейся в магнитном поле) длины проводника, так как длинный проводник может больше пересечь магнитных линий в секунду; - от величины синуса угла а между направлением движения проводника и направлением магнитного поля (рис. 93).
Рис. 93. Разложение скорости движения проводника в магнитном поле
Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: VH - составляющую, нормальную к направлению поля ( Величина индуктированной э. д. с. может быть найдена по формуле
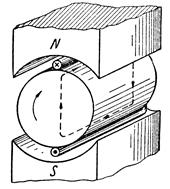
где В — величина магнитной индукции, Tл; l - активная длина проводника, м; V - скорость движения проводника, м/сек; α - угол пересечения. Как было отмечено выше, направление индуктированной э. д. с. зависит от направления движения проводника и от направления магнитного поля. Для определения направления индуктированной э. д. с. в проводнике, движущемся в магнитном поле, служит «правило правой руки». Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут показывать направление э. д. с, индуктированной в проводнике (рис. 94).
Рис. 94. Определение направления индуктированной э. д. с. в проводнике по «правилу правой руки»
В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной э. д. с. следует предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить также «правило правой руки».
Преобразование механической энергии в электрическую и обратно
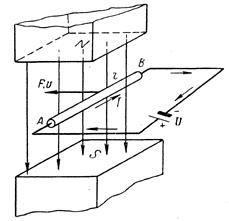
На законах электромагнитной индукции и электромагнитных сил основано действие электрических машин - генераторов, преобразующих механическую энергию в электрическую, и двигателей, преобразующих электрическую энергию в механическую. Обратимся к рис. 95. В магнитном поле между полюсами N и S помещен прямолинейный проводник. Если при помощи внешней механической силы F передвигать этот проводник перпендикулярно магнитным линиям поля, то в нем будет индуктироваться э. д. с.
Рис. 95. Преобразование механической энергии в электрическую
Напишем уравнение 2-го закона Кирхгофа для этой цепи:
где V - напряжение на зажимах, В; r - сопротивление проводника, Oм; I·r - падение напряжения в проводнике, В. Умножая почленно выражение (а) на I, получим
Так как
Учитывая, что
где РМЕХ = Е·I - механическая мощность, преобразуемая в электрическую; РЭЛ = U·I - электрическая мощность, отдаваемая во внешнюю цепь; ΔР = I2r - потери мощности (в виде тепла) в сопротивлении проводника. Рассмотрим теперь процесс преобразования электрической энергии в механическую. Пусть прямолинейный проводник АВ (рис. 96), по которому проходит ток I от источника напряжения, помещен во внешнее магнитное поле, образованное магнитом N - S. Если проводник неподвижен, то энергия источника напряжения расходуется исключительно на нагрев проводника:
Затрачиваемая мощность будет равна
откуда определяем ток в цепи:
Однако известно, что проводник с током, помещенный в магнитное поле, будет испытывать действие силы F со стороны поля, стремящейся перемещать проводник в магнитном поле в направлении, определяемом правилом левой руки. При своем движении проводник будет пересекать магнитные линии поля и в нем, по закону электромагнитной индукции, возникнет индуктированная э. д. с. Направление этой э. д. с, определенное по правилу правой руки, будет обратным току I. Назовем ее обратной э. д. с. ЕОБР. Величина ЕОБР согласно закону электромагнитной индукции будет равна
Рис. 96. Преобразование электрической энергии в механическую
По второму закону Кирхгофа, для замкнутой цепи имеем
или
откуда ток в цепи
Сравнивая выражения (а) и (в), видим, что в проводнике, движущемся в магнитном поле при одних и тех же значениях U и r, ток будет меньше, чем в неподвижном проводнике. Умножая почленно выражение (б) на I, получим
Так как
Учитывая, что
или
Последнее выражение показывает, что при движении проводника с током в магнитном поле мощность источника напряжения преобразуется в механическую мощность и частично в тепловую. Аналогичный процесс преобразования электрической энергии в механическую происходит в электрических двигателях. Рассмотренные выше примеры показывают, что электрическая машина обратима, т. е. может работать как генератор и как двигатель.
Правило Ленца
В 1834 г. русский академик Э. X. Ленц, известный своими многочисленными исследованиями в области электромагнитных явлений, дал универсальное правило для определения направления индуктированной э. д. с. в проводнике. Это правило, известное как правило Ленца, может быть сформулировано так: направление индуктированной э. д. с. всегда таково, что вызванный ею ток и его магнитное поле имеют такое направление, что стремятся препятствовать причине, порождающей эту индуктированную э. д. с. С учетом этого правила можно закон электромагнитной индукции выразить более общей формулой, позволяющей определить не только величину, но и направление индуктированной э. д. с:
Выражение Знак минус, стоящий перед выражением При увеличении магнитного потока выражение При равномерном изменении во времени магнитного потока выражение
Если катушка состоит из w витков, соединенных между собой последовательно, то индуктированная э.д.с. в ней равняется сумме э.д.с, индуктированных в отдельных витках:
Произведение числа витков катушки на сцепленный с ними магнитный поток называется потокосцеплением катушки и обозначается буквой ψ. Поэтому закон электромагнитной индукции можно записать и в другой форме:
Вихревые токи
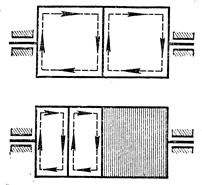
Рассматривая принцип действия генератора, мы видели, что при его вращении в проводниках обмотки якоря, пересекающих магнитное поле, индуктируется э. д. с. Так как и сам стальной якорь пересекает те же магнитные линии, то в нем, так же как и в проводнике, должны индуктироваться токи. Токи, которые индуктируются в массивных металлических телах при пересечении их магнитными линиями, называются токами, или токами Фуко. На рис. 97 схематически изображен якорь, вращающийся в магнитном поле. Вихревые токи в якоре, условно показанные пунктирными стрелками, проходя по телу якоря, будут нагревать его, на что затрачивается энергия. Если не принять мер к уменьшению вихревых токов, они, сильно нагревая якорь, могут привести к порче изоляции его обмотки. Устранить полностью потери на вихревые токи нельзя, но уменьшить их можно и нужно.
Рис. 97. Возникновение вихревых токов в сплошном стальном якоре электрической машины Для уменьшения потерь на вихревые токи якори генераторов, электрических двигателей и сердечники трансформаторов собирают из отдельных тонких (0,35 - 0,5 мм) штампованных листов мягкой стали, расположенных по направлению линий магнитного потока и изолированных один от другого лаком. Это делается для того, чтобы вследствие малого поперечного сечения каждого стального листа уменьшить величину проходящего через него магнитного потока, а стало быть, уменьшить индуктируемые в нем э. д. с. и ток. Путь вихревых токов в теле якоря при разделении последнего на отдельные изолированные участки схематически показан на рис. 98. Чтобы еще больше ослабить вихревые токи, увеличивают удельное сопротивление стали путем добавления в нее около 4% кремния. Такая сталь называется легированной.
Рис. 98. Изменение пути вихревых токов при разделении стального якоря электрической машины на изолированные участки (стрелками показаны направления индукционных токов)
Самоиндукция
В цепях электрического тока часто наблюдается особый вид электромагнитной индукции, называемой самоиндукцией. Рассмотрим подробнее это явление. Ранее было выяснено, что при всяком изменении магнитного потока, пронизывающего данный контур, в последнем индуктируется э. д. с.
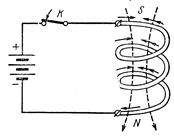
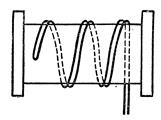
Это будет справедливо и для того случая, когда проводниковый контур будет пересекаться своим собственным магнитным потоком. Рассмотрим электрическую цепь, состоящую из катушки, источника тока и ключа К (рис. 99). При разомкнутом ключе тока в цепи нет. Магнитное поле катушки отсутствует. При замыкании ключа в цепи начинает проходить ток, создающий магнитный поток внутри катушки. Направление тока в витках катушки показано одинарной стрелкой. Появившийся магнитный поток катушки, увеличиваясь, будет пересекать витки катушки и согласно закону электромагнитной индукции в витках при этом возникает индуктированная э. д. с. Это явление называется самоиндукцией, а э. д. с, возникшая в результате самоиндукции, называется э. д. с. самоиндукции и обозначается еL. Величина э. д. с. самоиндукции определяется тем же уравнением
Рис. 99. Включение катушки к источнику с постоянной э. д. с.
Знак минус, стоящий в правой части уравнения, говорит о направлении индуктированной э. д. с, потому что в нем отображено правило Ленца. В самом деле, в момент замыкания цепи катушки появившийся ток вызовет возрастание магнитного потока катушки, т. е. поток получает положительное приращение (+ ΔФ). Э. д. с. самоиндукции получит отрицательное значение. Это означает, что э. д. с. самоиндукции, стремясь противодействовать возрастанию магнитного потока, будет иметь направление, противоположное э. д. с. (току) источника. Направление э. д. с. самоиндукции в момент замыкания цепи показано на рис. 99 двойной стрелкой. По истечении некоторого промежутка времени возрастающий магнитный поток катушки достигнет своего установившегося значения, прирост потока будет равен нулю (ΔФ = 0), индукция прекратится и э. д. с. самоиндукции исчезнет. Момент размыкания цепи с катушкой показан на рис. 100. Исчезающий ток, направление которого показано одинарной стрелкой, будет уменьшать магнитное поле катушки. Изменение поля вызовет появление э. д. с. самоиндукции в витках катушки. Убывание магнитного потока можно представить как отрицательное приращение потока (- ΔФ). Э. д. с. самоиндукции при этом получает положительное значение. Это означает, что, стремясь поддержать величину магнитного потока, противодействуя его убыванию, э. д. с. самоиндукции будет иметь направление, согласное с э. д. с. (током) источника. Это направление показано на рис. 100 двойной стрелкой.
Рис. 100. Отключение катушки от источника с постоянной э. д. с.
Необходимо заметить, что появление э. д. с. самоиндукции в катушке будет происходить не только в моменты включения или отключения цепи, но и при всяком изменении тока в цепи катушки.
Индуктивность
Магнитный поток, создаваемый током какого-либо витка при отсутствии намагничивающих сред (например, в воздухе), пропорционален величине тока:
где L - коэффициент пропорциональности, называемый индуктивностью. Единица измерения индуктивности - генри (Гн): 1 Гн = 103 миллигенри (мГн) = 106 микрогенри (мкГн). Индуктивность катушек зависит от числа витков, размера и формы катушек. Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов, индукционных катушек и т. п. Значительно меньшей индуктивностью обладают прямолинейные проводники. Короткие прямолинейные проводники, нити ламп накаливания, спирали электронагревательных приборов практически не обладают индуктивностью. На практике часто встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивление штепсельных реостатов и т. п.). В этом случае применяют бифилярную намотку катушки (рис. 101). Для этого проволоку перед намоткой сгибают вдвое и в таком виде навивают ее. Магнитный поток и индуктивность катушки с бифилярной намоткой равны нулю. Пусть мы имеем контур, состоящий из одного витка. В этом случае величина э. д. с. самоиндукции будет
Если ток в контуре изменился на Δi, то магнитный поток изменится на величину ΔФ:
Рис. 101. Бифилярная намотка катушки
Величина э. д. с. самоиндукции, которая возникнет в контуре, будет
Последнее выражение показывает, что величина э. д. с. самоиндукции зависит от индуктивности контура и скорости изменения тока в контуре. Отсюда можно дать определение единицы индуктивности - генри: индуктивностью в 1 генри обладает электрическая цепь, в которой при скорости изменения тока на 1 ампер в 1 секунду возникает э. д. с. самоиндукции, равная 1 вольту. Отдельные витки катушки в общем случае могут пронизываться различными магнитными потоками, поэтому общая э. д. с. катушки будет равна сумме э. д. с. отдельных витков:
Сумма магнитных потоков, сцепленных со всеми витками катушки, называется потокосцеплением и обозначается буквой ψ:
Поэтому выражение индуктивности катушки, состоящей из w витков, в отличие от индуктивности контура с w = 1 будет
Определим индуктивность кольцевой катушки. Выше нами было найдено выражение для магнитного потока кольцевой катушки:
Так как магнитный поток такой катушки сцеплен со всеми витками, то
откуда
С достаточной для практики точностью ту же самую формулу можно применять для определения индуктивности цилиндрической катушки (соленоида).
ОДНОФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Электротехнические устройства синусоидального тока
Электротехнические устройства синусоидального (переменного) тока находят самое широкое применение в различных областях техники и хозяйства: при генерировании, передаче и трансформировании электрической энергии, в электроприводе, бытовой технике, промышленной электронике, радиотехнике и т.п. Основные преимущества: 1) простота трансформирования 2) возможность получения источников большой мощности 3) дешевизна асинхронных двигателей
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.105.222 (0.007 с.) |

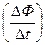 , пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е:
, пронизывающего проводящий контур (виток, рамку), сопровождается появлением в этом проводниковом контуре индуктированной э. д. с. е: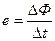
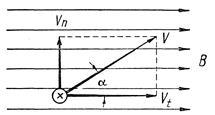
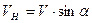 ), и Vt - тангенциальную составляющую (
), и Vt - тангенциальную составляющую (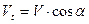 ), которая не принимает участия в создании э. д. с, так как при движении под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору В и не пересекал бы линий магнитной индукции.
), которая не принимает участия в создании э. д. с, так как при движении под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору В и не пересекал бы линий магнитной индукции.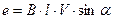

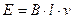 . Если концы проводника замкнуты на внешнее сопротивление, то по цепи потечет ток I, совпадающий по направлению с э. д. с. Е.
. Если концы проводника замкнуты на внешнее сопротивление, то по цепи потечет ток I, совпадающий по направлению с э. д. с. Е.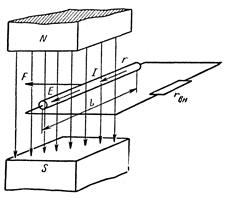
 (а)
(а)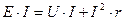

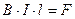 и
и 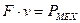 имеем
имеем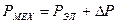 (б)
(б) Дж
Дж Вт
Вт (а)
(а)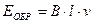
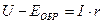
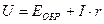 (б)
(б)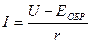 (в)
(в)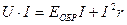

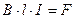 и
и 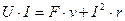
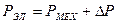
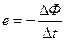
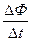 представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени Δt, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.
представляет собой среднюю скорость изменения магнитного потока по времени. Чем меньше промежуток времени Δt, тем меньше вышеуказанная э. д. с. отличается от ее действительного значения в данный момент времени.