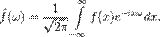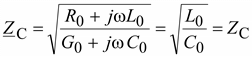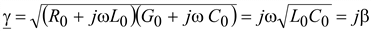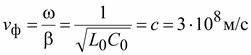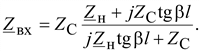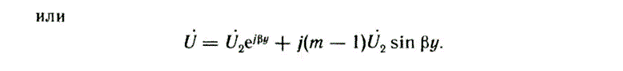Частотные характеристики параллельного колебательного контура.

В пар-ном колеб. контуре происходят колебания энергии между магнитными полями катушки и эл. полем конденсатора. В идеальном контуре при отключении его от источника эти колебания будут происходить бесконечно, в реальном – они затухают, но тем медленнее, чем выше добротность контура.

Влияние внутреннего сопротивления источника эл-ой энергии на хар-ки послед-ого и парал-го колебат. контуров.

Наличие внутреннего сопротивления источника энергии уменьшает эквивалентную добротность контура и снижает его избирательность. Поэтому с целью повышения избирательных свойств желательно, чтобы источник энергии, к которому, подключен контур, имел как можно меньшее внутреннее сопротивление, т. е. по свойствам приближался идеальному источнику напряжения.

Цепи с р.п. Первичные параметры длинной линии.

Цепь с распределёнными параметрами хар-ется протеканием в ней волновых процессов, при которых переменные величины тока и напряжения меняются не только во времени, но и в пространстве. В любой фикс-ный момент времени знач. напряжения либо тока может повторяться с определённым интервалом (длина волны). В такой цепи длина эл. цепи равна или больше длины волны.

Первичные параметры длинной линии:

-R - погонное сопротивление потерь

 

-L – погонная индуктивность

 

-g - погонная проводимость

-С - погонная ёмкость
Если параметры постоянны, то линия назыв. однородной.

 

49. Уравнения однородной длинной линии
Z =R +iwL

Y = g +iwC

Где Z и Y погонные комплексные сопротивление и проводимость линии, зависящие от частоты w

50. Установившийся синусоидальный режим в однородной линии:

Система уравнений:

-du’/dx=(R0+jwL0)*i=z0i

-di/dx=(g0+jwCo)U’=Y0u’

Z0-комплексное сопротивление

Y0 –комплексная проводимость: эти уравнения называют телеграфными. Они описывают з-н изменения амплитуды и фазы вдоль линии. Для решения телеграфных ур-й необходимо продифференцировать их по Х.

 

51.Линия без потерь и ее уравнения.

 

Линия без искажений представляет собой линию, вдоль которой волны всех частот распространяются с одинаковой фазовой скоростью и затухают в равной степени.Если сигналы, передаваемы по линиям связи являются не синусоидальными, но периодическими их можно разложить в тригонометрические ряды с помощью преобразования Фурье.

Если сигналы не синусоидальные и непериодические, то их можно разложить в непрерывный спектр. В этом случае прохождение сигнала по линиям проводят анализируя отдельных гармоник спектра.

53. Линия без потерь и её уравнения

Потери в линии отсутствуют, если Rо=0 и Go=0. Практически это означает, что активным сопротивлением проводов можно пренебречь, по сравнению с индуктивным, а активным сопротивлением между проводами по сравнению с емкостным. Для высокочастотных коротких линий, применяемых в радиотехнике зачастую пренебрегают Ro и Go по сравнению и wLo и wCo.

В линии без потерь волновое сопротивление не зависит от частоты. Базовая скорость при этом постоянна, следовательно линия без потерь не искажает сигнал.

Волновое сопротивление

Коэффициент распространения

Фазовая скорость

Входное сопротивление линии

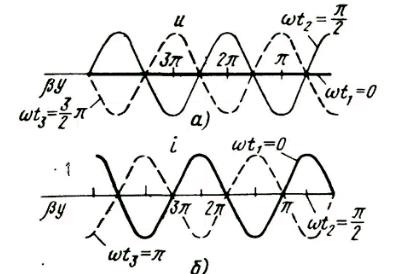
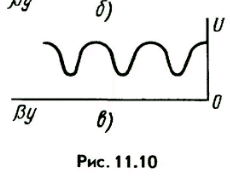
54. Стоячие волны в линии без потерь.

Стоячей волной называется процесс, получающийся от наложения прямой и обратной волн с одинаковыми амплитудами. Чем значительнее отличается сопротивление нагрузки от волнового сопротивления, тем заметнее становится отраженная волна. Режимы, при которых активная мощность в конце линии без потерь равна 0:

1) Холостой ход

2)Короткое замыкание

3)Чистореактивная нагрузка

В этих случаях падающая волна полностью отражается от нагрузки.

55.Бегущие волны в линии без потерь.Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны).Стоячая волна - частный случай бегущей волны, только бегущая волна переносит энергию вдоль линии. (стоячие волны 54 вопрос)

Вопрос №56. Смешанные волны в линии без потерь.