
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Білет 1 . Дії над комплексними числами, заданими в алгебраїчній формі.Содержание книги
Поиск на нашем сайте
Білет 1. Дії над комплексними числами, заданими в алгебраїчній формі. - сумою двох комплексних чисел
Білет 2. Поняття визначника ІІ і ІІІ порядку.Властивоста визначників. Означення. Визначником (детермінантом) другого порядку для системи двох рівнянь із двома невідомими Властивості визначників. 1,Величина визначника не зміниться, якщо його рядки зробити стовпцями, а стовпці – рядками, не змінюючи нумерації їх. 2,Якщо помножити всі елементи деякого стовпця (або рядка) на те саме число k, то значення визначника також помножаться на те саме число k. 3,Якщо у визначнику поміняти місцями рядки або стовпці, то визначник змінить знак на протилежний. 4,Якщо елементи двох рядків або стовпців однакові, то визначник дорівнює нулю.5,Величина визначника не змінюється, якщо до елементів одного рядка або стовпця додати елементи другого рядка або стовпця, помножені на те саме число.
Білет 3. Поняття диференціального рівняння та його розвязку. Диференціальним рівнянням називається рівняння, у яке входять: незалежна змінна
Значення довільних сталих знаходять при певних початкових значеннях аргументу і функції.
Білет 4. Дії над комплексними числами, заданими в показниковій формі. Дії над комплексними числами, заданими в показниковій формі. - добуток z1 i z2:
Білет 5. Визначеним інтеграл.Формула Ньоютона-Лейбніца. Визначеним інтегралом від функції 1. Визначений інтеграл від алгебраїчної суми скінченного числа функцій дорівнює алгебраїчній сумі визначених інтегралів від функцій, що додаються: 5. Відрізок інтегрування можна розбивати на частини: Для обчислення визначеного інтеграла від функції
Білет 6. Дії над комплексними числами, заданими в тригонометричній формі. - добуток z1 i z2: - частку знаходять так: - для добування кореня використовують формулу:
Білет 19. Еліпс. Еліпсом називається множина точок площини, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала
Білет 21. Гіпербола. Гіперболою називають множину точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називаються фокусами, є величина стала ( Якщо дійсна і уявна вісь гіперболи рівні (тобто Рівняння гіперболи, фокуси якої лежать на осі Оу, має вигляд: а рівняння її асимптот:
Білет 23. Парабола. Параболою називають множину точок на площині, рівновіддалених від даної точки, яку називають фокусом, і від даної прямої, яку називають директрисою.Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Ох і вітки напрямлені вправо, має вигляд: Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь О і вітки напрямлені вліво, має вигляд:
Білет 29. Коло Колом називається множина всіх точок площини, рівновіддалених від даної точки цієї площини, яка називається центром. Рівняння кола з центром у початку координат і радіусом Рівняння кола з центром у точці Рівняння кола в загальному вигляді записуютьтак:
Білет 1. Дії над комплексними числами, заданими в алгебраїчній формі. - сумою двох комплексних чисел
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.61 (0.007 с.) |

 і
і  називається комплексне число
називається комплексне число 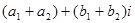 ; - добутком двох комплексних чисел
; - добутком двох комплексних чисел  ; - щоб виконати ділення двох комплексних чисел, ділене і дільник множать на комплексне число, спряжене дільнику.
; - щоб виконати ділення двох комплексних чисел, ділене і дільник множать на комплексне число, спряжене дільнику. називають число
називають число 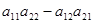 і записується так:
і записується так: 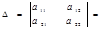
 записується так:
записується так:  і обчислюється за правилом трикутників:
і обчислюється за правилом трикутників:  .
.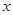 , шукана функція
, шукана функція  та її похідні або диференціали. Символічно диференціальні рівняння записують так:
та її похідні або диференціали. Символічно диференціальні рівняння записують так: 
 . Диференціальне рівняння називається звичайним, якщо шукана функція залежить від одного незалежного змінного. Порядком диференціального рівняння називається порядок старшої похідної або диференціала, що входить у дане рівняння. Розв’язком або інтегралом диференціального рівняння називається така функція, яка перетворює це рівняння в тотожність. Загальним розв’язком або загальним інтегралом диференціального рівняння називається такий розв’язок, до якого входить стільки незалежних довільних сталих, який порядок рівняння. Так, загальний розв’язок диференціального рівняння першого порядку має одну довільну сталу. Частинним розв’язком диференціального рівняння називається розв’язок, знайдений із загального при різних числових значеннях довільних сталих.
. Диференціальне рівняння називається звичайним, якщо шукана функція залежить від одного незалежного змінного. Порядком диференціального рівняння називається порядок старшої похідної або диференціала, що входить у дане рівняння. Розв’язком або інтегралом диференціального рівняння називається така функція, яка перетворює це рівняння в тотожність. Загальним розв’язком або загальним інтегралом диференціального рівняння називається такий розв’язок, до якого входить стільки незалежних довільних сталих, який порядок рівняння. Так, загальний розв’язок диференціального рівняння першого порядку має одну довільну сталу. Частинним розв’язком диференціального рівняння називається розв’язок, знайдений із загального при різних числових значеннях довільних сталих.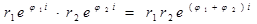 -частку знаходять так:
-частку знаходять так:  - при піднесенні до степеня:
- при піднесенні до степеня:  - для добування кореня використовують формулу:
- для добування кореня використовують формулу: 
 на відрізку [
на відрізку [  ;
; 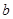 ] називається границя інтегральної суми при умові, що довжина найбільшого з елементарних відрізків прямує до нуля:
] називається границя інтегральної суми при умові, що довжина найбільшого з елементарних відрізків прямує до нуля: 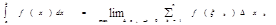 Для будь-якої функції
Для будь-якої функції  . Основні властивості визначеного інтеграла.
. Основні властивості визначеного інтеграла. .2. Сталий множник можна винести за знак визначеного інтеграла:
.2. Сталий множник можна винести за знак визначеного інтеграла: 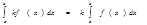 .3. При перестановці меж інтегрування визначений інтеграл змінює знак на протилежний
.3. При перестановці меж інтегрування визначений інтеграл змінює знак на протилежний  .4. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:
.4. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:  .
.  .
.  , є формула Ньютона-Лейбніца:
, є формула Ньютона-Лейбніца:  ,тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.
,тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування.
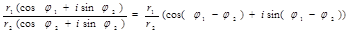 - при піднесенні до степеня використовують формулу Муавра:
- при піднесенні до степеня використовують формулу Муавра: 
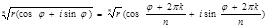
 , більша за відстань між фокусами
, більша за відстань між фокусами 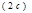 .
.  (6)
(6)  - Рівняння еліпса, фокуси якого лежать на осі Ох, де
- Рівняння еліпса, фокуси якого лежать на осі Ох, де 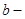 довжина малої півосі. Залежність між параметрами
довжина малої півосі. Залежність між параметрами  виражається співвідношенням:
виражається співвідношенням:  (7).Ексцентриситетом еліпса називається відношення фокусної відстані
(7).Ексцентриситетом еліпса називається відношення фокусної відстані 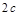 до великої осі
до великої осі 

 Якщо фокуси еліпса лежать на осі Оу, то його рівняння має вигляд:
Якщо фокуси еліпса лежать на осі Оу, то його рівняння має вигляд: 
 ), менша за відстань між фокусами (
), менша за відстань між фокусами ( ).Рівняння гіперболи, фокуси якої лежать на осі Ох, має вигляд:
).Рівняння гіперболи, фокуси якої лежать на осі Ох, має вигляд:  де
де  виражається співвідношенням:
виражається співвідношенням:  (11).Ексцентриситетом гіперболи називається відношення фокусної відстані
(11).Ексцентриситетом гіперболи називається відношення фокусної відстані  до її дійсої осі
до її дійсої осі 
 Гіпербола має дві асимптоти, рівняння яких
Гіпербола має дві асимптоти, рівняння яких  .
. ), то гіпербола називається рівносторонньою.
), то гіпербола називається рівносторонньою.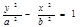 або
або  (16),
(16), (17).Гіперболи (10) і (16) називаються спряженими. Рівняння рівносторонньої гіперболи на осі Оу має вигляд:
(17).Гіперболи (10) і (16) називаються спряженими. Рівняння рівносторонньої гіперболи на осі Оу має вигляд:  .
.
 ), де
), де  -параметр параболи і відстань від фокуса до директриси. Рівняння її директриси
-параметр параболи і відстань від фокуса до директриси. Рівняння її директриси  .
. (19), де
(19), де  .Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:
.Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:  (20), де
(20), де  -параметр параболи і відстань від фокуса до директриси. Рівняння її директриси
-параметр параболи і відстань від фокуса до директриси. Рівняння її директриси  . Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:
. Рівняння параболи з вершиною в початку координат, віссю симетрії якої є вісь Оу і вітки напрямлені вгору, має вигляд:  (20), де
(20), де 

 має вигляд:
має вигляд:  (1)
(1) і радіусом
і радіусом  має вигляд:
має вигляд:  (2)
(2) (3)
(3)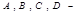 сталі коефіцієнти.
сталі коефіцієнти.


