Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні відомості про комплексні числа.
Будь-яке комплексне число алгебраїчною – показниковою – В алгебраїчній формі запису зручно додавати та віднімати комплексні числа. Наприклад:
Перемножувати та ділити комплексні числа зручно в показниковій формі запису. Тому перед виконанням даних дій слід виразити комплексні числа в показниковій формі. Перехід від алгебраїчної до показникової форми запису виконується за формулами: Наприклад:
При визначенні кутів зверніть увагу, що комплексне число Після запису комплексних чисел в показниковій формі їх добуток та частка розраховується так:
Якщо необхідно знову знайти суму або різницю чисел, які записані в показниковій формі, необхідно виконати зворотній перехід. Перехід від показникової до алгебраїчної форми запису виконується за формулою, в основі якій лежить формула Ейлера Наприклад:
6· ej 160,4 = –5,65+j2; 20· e-j80,5 = 8,25 – j19,7; 5· e-j120 = –2,5–j4,3.
Додаток 2 Загальні положення
Дане видання містить завдання до двох розрахунково-графічних робіт (РГР), що передбачено програмою курсу “Електротехніка та електромеханіка”. Першу РГР (задачі № 1…3) виконують паралельно вивченню теоретичної частини "Електричні кола"; задачі № 4 та 5 – частини "Електричні машини".
Задача №1 Розрахунок електричного лінійного кола постійного струму
Згідно заданого викладачем варіанту завдання (табл. 1.1, …, 1.4) виконати розрахунок параметрів електричного кола, а саме: 1.Задатися довільно вибраними позитивними напрямками струмів у вітках між вузлами, позначити їх стрілками і підписати. 2. Розрахувати значення струмів у вітках та значення електрорушійної сили, якщо їх величини не задані у висхідних даних.
3. Розрахувати потужність енергії, що генерується джерелом напруги. 4. Розрахувати потужності, які споживаються кожним приймачем енергії. 5. Перевірити баланс потужностей. 6. Позначити усі вузли кола літерами і визначити їх потенціали відносно одного з вузлів кола, величину потенціалу якого прийняти рівною нулю.
Таблиця 1.1
Таблиця 1.2
Таблиця 1.3
Таблиця 1.4
Рис. 1 Рис. 2
Рис. 3 Рис. 4
Рис. 5 Рис. 6
Рис. 7 Рис. 8
Рис. 9 Рис. 10
Рис. 11 Рис. 12
Рис. 13 Рис. 14
Рис. 15 Рис. 16
Рис. 17 Рис. 18
Рис. 19 Рис.20
Рис.21 Рис. 22
Рис.23 Рис. 24 Задача №2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.45 (0.058 с.) |
можна виразити різними формами:
, де а – дійсна частина комплексного числа (дорівнює проекції вектора 
на вісь “ х ”) і jb – уявна частина комплексногочисла (b дорівнює проекції вектора 
на вісь “ у ”);
, де С – модуль комплексного числа (дорівнює довжині вектора 
– аргумент комплексного числа, який дорівнює величині кута між вектором 
, 
;
;
.
; 
.
;
;
;
.
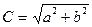знаходиться у другому квадранті комплексної площини, 
в третьому квадранті площини, а аргумент 
.
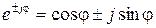, а саме: 
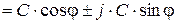, де 
; 
