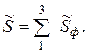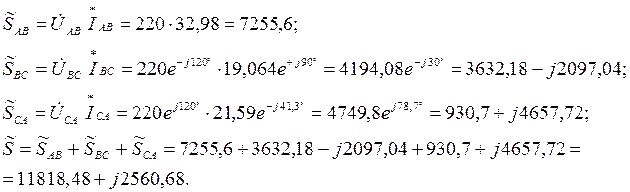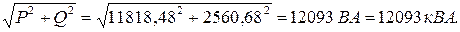Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок балансу потужностейСодержание книги Поиск на нашем сайте
Рівняння балансу потужностей для складної схеми буде мати вигляд:
Алгебраїчна сума потужностей всіх джерел енергії повинна дорівнювати арифметичній сумі потужностей всіх споживачів енергії. При цьому, якщо напрямок струму співпадає з напрямком дії ЕРС, потужність джерела необхідно рахувати додатньою і записувати в рівнянні із знаком “+”. У протилежному випадку цю потужність рахують від¢ємною і записують із знаком “-“. Запишемо для цього кола рівняння балансу потужностей:
Лінійні електричні кола однофазного змінного струму Окремі теоретичні положення
Миттєве значення ЕРС, що змінюється у часі по синусоїдному закону, має вигляд: По такому самому закону будуть змінюватись викликані нею струми і напруги в вітках електричного кола. В електричних колах змінного струму крім активних опорів присутні ще і реактивні (індуктивні і ємнісні) величини яких залежать від кутової частоти струму Наявність в електричному колі реактивних опорів, індуктивності та ємності призводять до зсуву фаз між струмами та напругами, а саме – миттєва напруга на активному опорі дорівнює и= і·R і збігається по фазі із струмом. На індуктивності напруга Якщо в вітках електричного кола присутні активні і реактивні опори, то перший та другий закони Кірхгофа в колах змінного струму можна застосовувати тільки для миттєвих значень, а розрахунок миттєвих значень струмів та напруг, навіть в простих колах, є досить громіздкою задачею. При послідовному з’єднанні елементів в електричному колі, що містить активні та реактивні опори, діюче значення струму джерела розраховується по формулі:
де U – діюче значення напруги на затискачах джерела, Z, R екв, X екв – повний опір, еквівалентні активний та реактивний опори кола відповідно. В колах з паралельним з’єднанням елементів струм джерела дорівнює:
де Y, g екв, в екв – повна провідність, еквівалентні активна та реактивна провідності кола відповідно. Кут зсуву фаз між напругою та струмом джерела розраховується за формулами:
Активна потужність енергії – Реактивна потужність енергії – Повна потужність – Баланс потужностей в електричному колі змінного струму має вигляд:
2.2. Символічний метод (метод комплексних амплітуд) розрахунку електричних кіл змінного струму
Розрахунок електричних кіл змінного струму спрощується, якщо синусоїдні величини зображувати векторами або комплексними числами. Наприклад, електрорушійна сила, миттєве значення якої Підставою для такого зображення є те, що якщо даний вектор обертати проти руху годинникової стрілки з кутовою швидкістю Так само зображуються і решта синусоїдних величин в колі (струми, напруги), які викликані дією ЕРС Оскільки всі вектори при однаковій частоті будуть обертатися з однією і тією ж швидкістю, то їх взаємне розташування в часі не змінюється. Тому такі вектори можна розглядати в системі координат в певний момент часу, як правило при t =0, як сукупність нерухомих векторів, яка називається векторною діаграмою. Векторна діаграма дає змогу досить просто розраховувати електричні параметри в електричних колах графічним методом. Але метод векторних діаграм, як і всі графічні методи особливо в складних колах, призводить до похибок в розрахунках.
Задача значно спрощується, якщо вісь “ х ” вважати віссю дійсних чисел, а вісь “ у ” віссю уявних чисел комплексної площини. Тоді на такій площині положення векторів можна зафіксувати комплексними числами, наприклад вектор 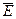 буде відповідати комплексному числу буде відповідати комплексному числу 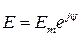 , рис.2.1,в. , рис.2.1,в.Так само комплексними числами зображуються і інші величини електричного кола, що змінюються в часі синусоїдно. Наприклад, вираз для діючого значення електрорушійної сили, що змінюється в часі синусоїдно Прояв електромагнітних явищ, які обумовлюються реактивними елементами кола (зсув по фазі Такі символічні зображення величин, що змінюються в часі синусоїдно, та зображення опорів комплексними числами дають можливість співвідношення між синусоїдними величинами та інтегро-диференціальні рівняння, складені за законами Кірхгофа в колах змінного струму, замінити простими алгебраїчними співвідношеннями комплексних чисел або рівняннями з комплексними коефіцієнтами. Після такої заміни в символічній формі запису виконуються необхідні розрахунки, а потім, якщо необхідно, виконують зворотній перехід до оригіналів, тобто до записів виразів миттєвих значень величин. Докладніше розрахунок параметрів електричних кіл змінного струму розглянемо на конкретних прикладах №4 і №5.
Приклад №.4 Послідовно з конденсатором, ємність якого С =318,47 мкФ, включені дві котушки індуктивностей з параметрами L 1=0,034 Гн, R 1= 3 Ом, L 2= 25,92 мГн, R 2=1 Ом. До даного електричного кола підведена напруга, миттєве значення якої – діюче значення струму; – діюче значення напруг на окремих елементах кола; – повну, активну та реактивну потужності електричної енергії, що споживаються електричним колом; – побудувати векторну діаграму струму та напруг; – записати вираз миттєвих значень струму.
Схема електричного кола згідно умови задачі представлена на рис.2.2. Аналізуючи умову задачі, з’ясовуємо, що кутова частота підведеної напруги (див. запис миттєвого значення напруги)
Зверніть увагу, що при розрахунках опорів величини ємності та індуктивностей переводяться в основні одиниці виміру згідно системи СІ (С – [Ф], L – [Гн]). Розрахунок простих електричних кіл, а дане коло є просте, можна виконати так: За законом Ома діюче значення струму Діюче значення напруги дорівнює
Еквівалентний опіp при послідовному з’єднанні елементів розраховується за формулою:
Тоді діюче значення струму дорівнює:
Але за цим методом необхідно окремо розраховувати ще й кут зсуву між струмом і напругою, який залежить від характеру загального опору.
Оскільки загальний опір кола має активно-індуктивний характер, то струм буде відставати від напруги на кут Вираз для миттєвого значення струму:
Активна потужність, що споживається електричним колом, розраховується за формулою:
Реактивна потужність:
Повна потужність:
Ці самі потужності розраховуються ще і за такими формулами:
Для побудови векторної діаграми необхідно розрахувати по закону Ома діючі значення спадів напруг на окремих елементах електричного кола: UC=I·XC = 11,38·10 = 113,8 B; UR1=I·R1 = 11,38·3 = 34,14 B; UL1=I·XL1 = 11,38·10,7 = 121,76 B; UR2=I·R2 = 11,38·1 = 11,38 B; UL2=I·XL2 = 11,38·3,14 = 35,73 B Векторну діаграму будуємо в такій послідовності: 1. Орієнтуючись на числові значення струму та спадів напруг вибираємо масштаби для векторів струму та напруг: – 1см. довжини вектора струму буде відповідати 2 А, – 1см. довжини векторів напруг буде відповідати 20В. 2. На площині довільно креслимо вісь дійсних чисел відносно якої під кутом -35,55˚(що відповідає -35˚33’) в напрямку руху годинникової стрілки відкладаємо вектор струму 3 Відносно вектора струму відкладаємо вектора спадів напруг на окремих елементах електричного кола. Вектор напруги на ємності орієнтують під кутом 90˚ відносно вектора струму в сторону відставання. Вектора напруг на активних опорах
отримаємо вектор загальної напруги Векторна діаграма має вигляд як на рис.2.3.
Приклад 5 Задачу, яка задана в прикладі №4, розрахуємо символічним методом. Якщо застосувати символічний метод, то розрахунок зводиться до таких дій над комплексними числами: 1. Записуємо комплексним числом діюче значення напруги, миттєве значення якої
2. Опори елементів кола також зображуємо комплексними числами. Опір ємності Повні комплексні опори котушок індуктивностей
3. Еквівалентний опір кола в символічному зображенні має вигляд
4. Діюче комплексне значення струму визначається за формулою
Вираз миттєвого значення струму має вигляд: 5. Комплексна потужність
В цьому виразі дійсна частина комплексного числа
Приклад №6 Параметри електричного кола, яке зображене на рис.2.4, задані у вигляді комплексних чисел:
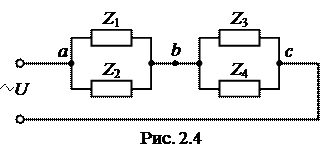
Необхідно: – накреслити принципову схему електричного кола; – розрахувати комплексні струми в вітках електричного кола і записати вирази їх миттєвих значень; – скласти і розрахувати баланс потужностей в електричному колі; – побудувати векторну діаграму струмів та топографічну діаграму напруг. Аналізуючи вирази опорів, записаних в символічній формі, приходимо до висновку, що в ділянці кола «ab» паралельно між собою включені резистор з активним опором R 1= 34Ом та ідеальна котушка індуктивності, індуктивний опір якої XL 2=8,5Ом а ділянка електричного кола «вс» складається із двох паралельно включених віток, кожна з яких має активні і реактивні елементи. В одній із віток послідовно включені резистор з опором R 3 = 2 Ом та конденсатор з реактивним ємнісним опором XС 3=5 Ом і відповідно в іншій паралельній вітці включені R 4 =3 Ом та XL 4 =4 Ом. Отже схема електрична принципова буде мати вигляд як на рис.2.5.
Дане електричне коло є простим, оскільки в ньому присутнє тільки одне джерело напруги. Такі кола, як правило, розраховуються шляхом еквівалентних перетворень схеми і зведенням її до одного еквівалентного опору Zекв, рис.2.6. В електричному колі, яке складається тільки із джерела струму та одного еквівалентного опору (рис.2.6,б) струм І 1 розраховується по закону Ома. Оскільки розрахунки будемо виконувати символічним методом то закон Ома записується так:
де
Тому 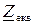 = = 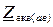 + + 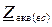 , де , де 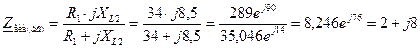 , ,
Загальний еквівалентний комплексний опір електричного кола дорівнює:
При виконанні розрахунків доцільно операції „додавання” та „віднімання” комплексних чисел виконувати в алгебраїчній формі запису, а при множенні та діленні комплексних чисел переводити комплексні числа в показникову форму. Як виконується перехід від однієї форми запису до іншої викладено в додатку № 1 в теоретичних відомостях про комплексні числа. Отже діюче комплексне значення струму в нерозгалуженій частині кола дорівнює:
Величини струмів в паралельних вітках можна визначати різними шляхами. Наводимо один із них. Розраховуємо напруги на паралельних вітках між вузлами «a» і «b» та «b» і «с». Згідно рис 7 .
Тоді струми в паралельних вітках розраховуються за законом Ома для окремих ділянок електричного кола:
Перевірку правильності розрахунку можна виконати по I закону Кірхгофа або по балансу потужностей. Рівняння, складені по першому закону Кірхгофа для вузлів «а» і «b» даного кола, мають вигляд:
Наприклад, Виконавши розрахунок кола символічним методом визначаємо діючі значення струмів в вітках: I = 12,032 A, І 1 =2,917 А, І 2 =11,672 А, I 3 = 11,797 A, I 4 = 12,706 A. Оскільки максимальне значення струму
Повна потужність енергії, яку джерело віддає в електричне коло, в символічному методі розраховується за формулою:
де
Якщо даний вираз комплексної потужності перевести в алгебраїчну форму, то дійсна частина комплексної потужності буде дорівнювати активній потужності, а уявна частина - реактивній потужності.
З іншого боку, активна потужність, яка використовується споживачами дорівнює
а реактивна потужність, яка використовується споживачами Q = Приклад розрахований правильно. Похибка розрахунку складає менше дозволених 3%. Наприклад:
Побудова векторної діаграми Перед побудовою векторної діаграми необхідно розрахувати діючі значення спадів напруг на окремих елементах кола (по закону Ома). UR 1 = UL 1= I 1· R 1= I 2· XL 2=2,917∙34 = 11,672·8,5=99,2 B; UС 3 = I 3· XС 3= 11,797∙5 = 58,98 B; UR 3 = I 3· R 3= 11,797∙2 = 23,59 В UL 4 = I 4· X L4= 12,706∙4 = 50,82 B; UR 4 = I 4· R 4= 12,706∙3 = 38,12 В Побудову векторної діаграми (рис.2.7) виконуємо в такому порядку: 1. Проаналізувавши величини діючих значень струмів та напруг вибираємо зручні для побудови масштаби, а саме: 1 см. довжини вектора струму відповідає 2 А, а 1см. довжини вектора напруги відповідає 10 В. 2. На площині в довільному напрямку (як правило, горизонтально) креслимо вісь дійсних чисел. Приймемо потенціал вузла „с” електричного кола рівним нулю і позначимо його на осі дійсних чисел Vс= 0. З точки „ с ” відкладаємо вектор вхідної напруги. Оскільки початкова фаза заданої вхідної напруги 3.Відносно осі дійсних чисел, а в даному випадку відносно вектора вхідної напруги, будуємо в вибраному масштабі вектор загального струму 4. Потім будуємо, в вибраному для напруги масштабі, векторну діаграму спадів напруг. Рекомендується при побудові векторів напруг обхід в контурі або на ділянці кола вибирати проти напрямку струму в вітках і відкладати вектора спадів напруг на елементах кола в тій самій послідовності, в якій відповідні елементи розташовані в електричному колі. Тоді кінець кожного вектора спаду напруги на комплексній площині буде відповідати потенціалу відповідних точок електричного кола. Починаємо побудову векторної діаграми від вузла „с” електричного кола. Оскільки напруги на активних опорах співпадають по фазі із струмами, які протікають по відповідних опорах, а напруги на реактивних опорах випереджають або відстають (залежно від характеру реактивного опору) на кут Згідно другого закону Кірхгофа в даному колі, загальна напруга дорівнює векторній сумі спадів напруг В результаті побудови діаграми даного кола отримали вектор загальної напруги
Трифазні кола Теоретичні положення Трифазною системою змінного струму називають сукупність трьох (зв’язаних або незв’язаних) однофазних кіл, в яких діють три електрорушійні сили (ЕРС) однакової частоти, зсунуті за фазою одна відносно іншої. Три електрорушійні сили створюються спеціальними трифазними генераторами. Такі генератори на статорі мають три однакові обмотки (фази), які в просторі зсунуті на кут Створена при цьому система ЕРС буде симетричною з прямою послідовністю фаз і записується так:
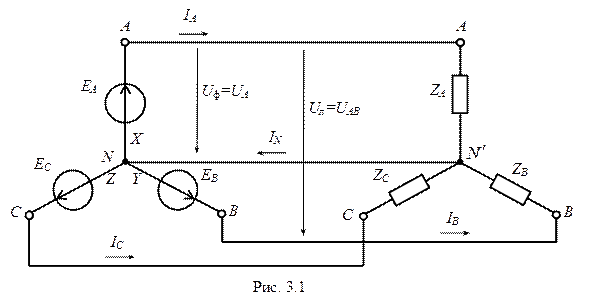
Примітка. Термін «фаза» в трифазних колах має два різних значення: а) поняття, що характеризує стадію, момент періодичного процесу; б) назву частини електричного трифазного кола. Фази трифазного генератора можуть бути з’єднані за схемою «трикутник» або «зірка». За такими схемами з’єднуються і споживачі, а разом із генератором вони створюють одне трифазне складне розгалужене коло яке може бути розраховане будь яким методом розрахунку складних кіл змінного струму. Але, враховуючи специфічні особливості трифазних кіл, розрахунки величин струмів, напруг, потужностей значно спрощуються. Якщо комплексні опори усіх фаз однакові, тобто трифазне коло симетричне, то достатньо розрахунки виконати тільки в одній фазі. Струми в інших фазах будуть однаковими по величині і зсунуті між собою на кут При різному навантаженні фаз розрахунки фазних струмів необхідно виконувати для кожної фази окремо. При з’єднанні обмоток генератора «зіркою» (рис. 3.1) кінці їх (x, y, z) з’єднуються в один вузол «N», який називають нульовою точкою генератора. При такому з’єднанні на виході генератора маємо два різних діючих значень напруги: лінійні (U л)- між затискачами генератора А, В, С, а саме UАВ , UВС , СА і фазнінапруги (U ф) між затискачами генератора А, В, С і нульовою точкою генератора N,тобто UА0, UВ0, UС0, інакше UА, UВ, UС. В симетричній трифазній системі між діючими значеннями лінійної та фазної напруги існує співвідношення: При підключенні до затискачів генератора споживачів, які також з’єднані «зіркою», необхідно нульові точки генератора і споживачів з’єднати четвертим проводом, який називають нульовим (або нейтральним). При з’єднанні «зіркою» лінійний і фазний струм завжди будуть однаковими і тому І ф =І л. Діюче значення струму в нейтральному проводі позначають І 0або ІN . Згідно І закону Кірхгофа діюче значення струму в нейтральному проводі дорівнює геометричній сумі фазних струмів
При з’єднанні споживачів «трикутником» фазна напруга споживачів дорівнює відповідній лінійній напрузі генератора  (рис.3.2) (рис.3.2)
Фазні струми при різних опорах фазних споживачів розраховуються за законом Ома в кожній фазі окремо, тобто Якщо навантаження в фазах однакові, тобто При нерівномірному навантаженні лінійні струми будуть різними і в цьому випадку знаходяться згідно І закону Кірхгофа як різниця відповідних комплексних фазних струмів
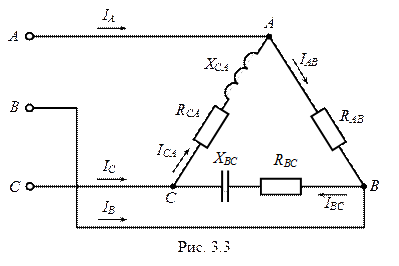
Розглянемо на конкретних прикладах розрахунок трифазних кіл при різних способах з’єднання та різних видів навантаження. Приклад № 7 Трифазний споживач (рис.3.3) підключений до симетричного генератора, лінійна напруга якого U л = 220В. Розрахувати фазні і лінійні струми, а також повну потужність (потужність усіх трьох фаз) споживачів, з’єднаних «трикутником», якщо задано RАВ = 6,67 Ом, RВС = 10 Ом, XВС = 5,77 Ом, RСА = 2 Ом, X СА = 10 Ом. Побудувати векторну діаграму напруг і струмів.
Розрахунок задачі будемо виконувати символічним методом. Якщо прийняти
Комплексні струми в фазах при нерівномірному навантаженні розраховуються таким чином:
Комплексні лінійні струми визначаються як різниця відповідних фазних комплексних струмів.
Комплексна повна потужність однієї фази Комплексна повна потужність всього трифазного кола Отже:
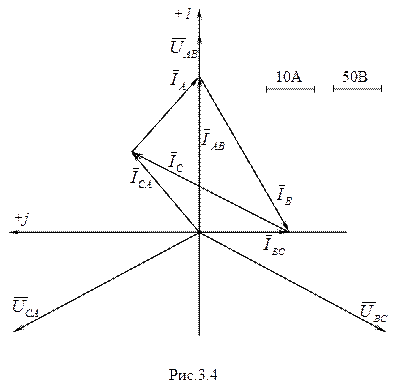
S = Векторна діаграма при нерівномірному навантаженні споживачів, з’єднаних «трикутником» має вигляд, який зображений на рис.3.4:
Приклад № 8 До симетричного трифазного генератора, діюче значення лінійної напруга якого дорівнює U л= 380В, підключений трифазний споживач з’єднаний «зіркою» з нейтральним проводом (рис.3.5) Визначити струм в нейтральному проводі, якщо параметри фазних споживачів дорівнюють таким величинам: | |||||||||||||||||||||||
|
| Поделиться: |

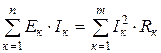 , де к - порядковий номер вітки, n – кількість джерел в електричному колі, m –кількість віток.
, де к - порядковий номер вітки, n – кількість джерел в електричному колі, m –кількість віток.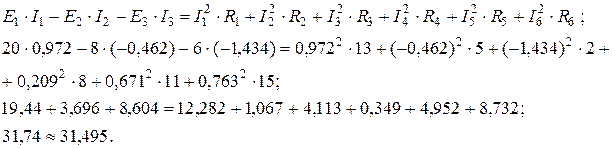 Відносна похибка розрахунку складає
Відносна похибка розрахунку складає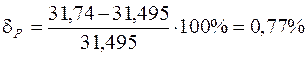 , що менше дозволеної 3% похибки.
, що менше дозволеної 3% похибки. де Ет – максимальне значення електрорушійної сили,
де Ет – максимальне значення електрорушійної сили, 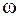 – кутова частота, t – час (мить), в який визначається миттєве значення,
– кутова частота, t – час (мить), в який визначається миттєве значення, 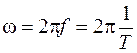 ,
, 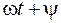 –фаза або фазний кут в момент часу t,
–фаза або фазний кут в момент часу t,  дорівнює фазі в початковий момент (при t =0) і тому називається початковою фазою.
дорівнює фазі в початковий момент (при t =0) і тому називається початковою фазою.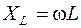 ,
, 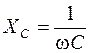 .
.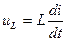 випереджає струм на кут
випереджає струм на кут  , а на ємності напруга
, а на ємності напруга 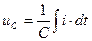 відстає від струму на кут
відстає від струму на кут 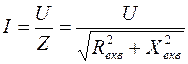 ,
,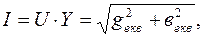
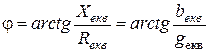 .
.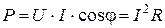 , Вт;
, Вт;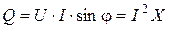 , ВАр;
, ВАр;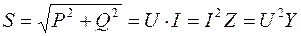 , ВА.
, ВА.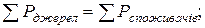

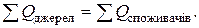
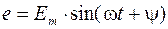 , рис 2.1, a, в прямокутній системі координат можна зобразити вектором
, рис 2.1, a, в прямокутній системі координат можна зобразити вектором  – рис.2.1,б, довжина якого (згідно обраного масштабу) дорівнює максимальному Ет (або діючому
– рис.2.1,б, довжина якого (згідно обраного масштабу) дорівнює максимальному Ет (або діючому  ) значенню ЕРС і який розташований відносно горизонтальної осі “ x ” під кутом початкової фази
) значенню ЕРС і який розташований відносно горизонтальної осі “ x ” під кутом початкової фази 
 в комплексній формі запису має вигляд
в комплексній формі запису має вигляд  .
. між струмом та напругою), в символічному методі врахований, а саме, спад напруги
між струмом та напругою), в символічному методі врахований, а саме, спад напруги  на індуктивному опорі
на індуктивному опорі 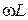 помножується на оператор повороту на 90˚, тобто на j =
помножується на оператор повороту на 90˚, тобто на j = 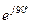 , а спад напруги на ємнісному опорі
, а спад напруги на ємнісному опорі 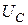 необхідно помножити на оператор
необхідно помножити на оператор  . Тоді напруги на індуктивності та ємності в символічному методі записуються як
. Тоді напруги на індуктивності та ємності в символічному методі записуються як  і
і 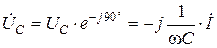 відповідно. В цих виразах множники
відповідно. В цих виразах множники 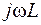 та
та  є реактивними опорами індуктивності та ємності, що записані в комплексній формі.
є реактивними опорами індуктивності та ємності, що записані в комплексній формі.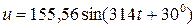 .Необхідно накреслити схему електричного кола та розрахувати:
.Необхідно накреслити схему електричного кола та розрахувати: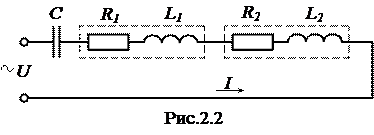
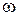 = 314 рад/сек. На такій частоті опори реактивних елементів електричного кола дорівнюють:
= 314 рад/сек. На такій частоті опори реактивних елементів електричного кола дорівнюють: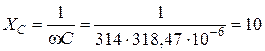 Ом;
Ом;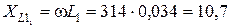 Ом;
Ом;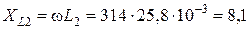 Ом.
Ом. , де U –діюче значення підведеної напруги, а Z екв – еквівалентний опір електричного кола.
, де U –діюче значення підведеної напруги, а Z екв – еквівалентний опір електричного кола.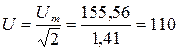 В.
В.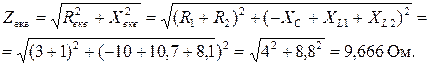
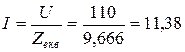 А
А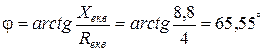 .
.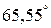 .
.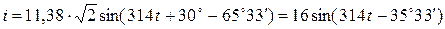 .
.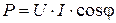 = 110·11,38·cos
= 110·11,38·cos 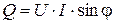 = 110·11,38·sin65,55˚ = 1138,542 ВАр.
= 110·11,38·sin65,55˚ = 1138,542 ВАр.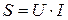 = 110·11,38 = 1251,8 ВА.
= 110·11,38 = 1251,8 ВА.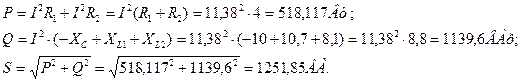
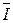 . Довжина вектора в вибраному для струму масштабі дорівнює 5,69 см.
. Довжина вектора в вибраному для струму масштабі дорівнює 5,69 см.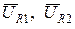 співпадають по напрямку з вектором струму, а вектори спадів напруг на індуктивностях
співпадають по напрямку з вектором струму, а вектори спадів напруг на індуктивностях 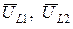 випереджають вектор струму
випереджають вектор струму 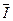 на кут 90˚.В результаті складання векторів напруг:
на кут 90˚.В результаті складання векторів напруг: =
= 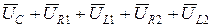
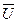 , який буде розташований під кутом 30˚ проти руху годинникової стрілки і довжина якого в вибраному для напруги масштабі буде дорівнювати 5,5 см.
, який буде розташований під кутом 30˚ проти руху годинникової стрілки і довжина якого в вибраному для напруги масштабі буде дорівнювати 5,5 см.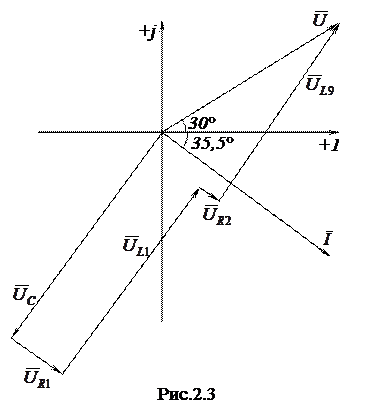
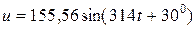
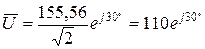 .
.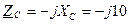 ;
; та
та 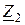

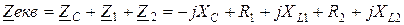 =
= 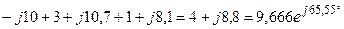 .
.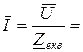
 =
= 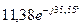 .
.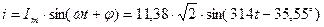 .
.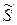 розраховується за формулою:
розраховується за формулою: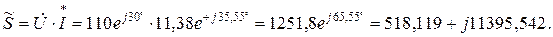
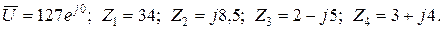
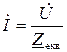 ,
, - еквівалентний комплексний опір кола, яке складається із двох послідовно включених ділянок кола „ аb” та „bс”.
- еквівалентний комплексний опір кола, яке складається із двох послідовно включених ділянок кола „ аb” та „bс”.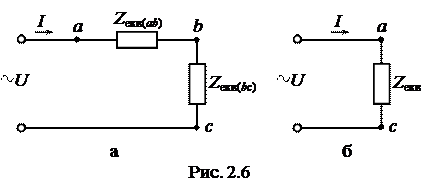
 .
. =
= 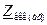 +
+ 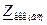 = 2+j8 +5,268-j0,346= 7,268+j7,654 = 10,555 e j46,48.
= 2+j8 +5,268-j0,346= 7,268+j7,654 = 10,555 e j46,48.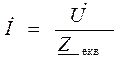 =
= 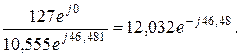
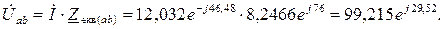
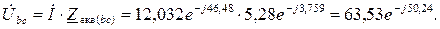
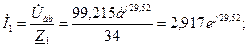
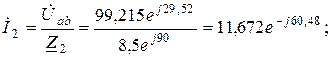
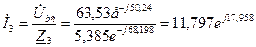 ;
;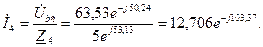
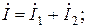
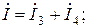
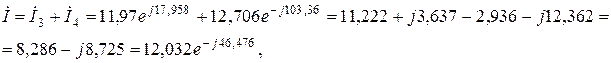 що приблизно дорівнює значенню струму
що приблизно дорівнює значенню струму 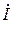 , розрахованому по закону Ома для еквівалентної схеми. Допустима похибка розрахунку дорівнює 3%.
, розрахованому по закону Ома для еквівалентної схеми. Допустима похибка розрахунку дорівнює 3%.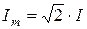 , то вирази миттєвих значень струмів мають вигляд:
, то вирази миттєвих значень струмів мають вигляд: ;
;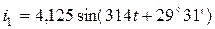

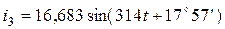 ;
;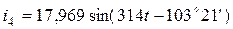 .
.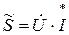 ,
,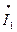 вираз струму, що спряжений виразу
вираз струму, що спряжений виразу 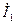 .
. 1528,064 e j 46,481 = 1052,217 + j 1108,069.
1528,064 e j 46,481 = 1052,217 + j 1108,069. Р =
Р = 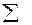 Іk 2· Rk = I 12 · R 1 + I 32 · R 3+ + I 42 · R 4 = 2,9172 ·34 + 11,7972·2 + 12,7062·3 = 289,302+278,338 + 484,327 = 1052 Вт,
Іk 2· Rk = I 12 · R 1 + I 32 · R 3+ + I 42 · R 4 = 2,9172 ·34 + 11,7972·2 + 12,7062·3 = 289,302+278,338 + 484,327 = 1052 Вт,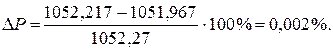
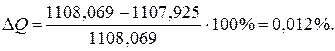
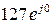 дорівнює нулю, то вектор вхідної напруги, довжина якого в вибраному масштабі дорівнює 12,7 см, буде співпадати по напрямку з віссю дійсних чисел.
дорівнює нулю, то вектор вхідної напруги, довжина якого в вибраному масштабі дорівнює 12,7 см, буде співпадати по напрямку з віссю дійсних чисел. та вектора струмів
та вектора струмів  . Кути зсуву між вхідною напругою і струмами записаний в виразах миттєвих значень відповідних струмів. Наприклад, згідно результату розрахунку, струм І відстає від напруги на кут
. Кути зсуву між вхідною напругою і струмами записаний в виразах миттєвих значень відповідних струмів. Наприклад, згідно результату розрахунку, струм І відстає від напруги на кут  і тому вектор струму
і тому вектор струму 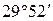 і тому вектор струму
і тому вектор струму  креслимо в сторону проти руху годинникової стрілки відносно вектора напруги. Аналогічно під відповідними кутами, які зазначені в виразах миттєвих значень струмів, креслимо на векторній діаграмі вектора струмів
креслимо в сторону проти руху годинникової стрілки відносно вектора напруги. Аналогічно під відповідними кутами, які зазначені в виразах миттєвих значень струмів, креслимо на векторній діаграмі вектора струмів 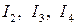 . Після побудови усіх векторів струмів доцільно графічно перевірити І закон Кірхгофа для вузлів «а» і «b».
. Після побудови усіх векторів струмів доцільно графічно перевірити І закон Кірхгофа для вузлів «а» і «b».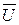 R 2 креслимо співпадаючим із вектором струму
R 2 креслимо співпадаючим із вектором струму 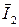 , а вектор
, а вектор 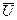 C 2 креслимо під кутом 90˚ до вектора струму
C 2 креслимо під кутом 90˚ до вектора струму 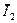 в сторону руху годинникової стрілки. Сума векторів
в сторону руху годинникової стрілки. Сума векторів 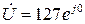

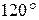 . Крайні точки фазних обмоток називають «початками» А, В, С і, відповідно, «кінцями». X, Y, Z. Всередині статора розташований ротор на обмотки якого подається постійний струм і таким чином створюється магнітне поле. Якщо ротор обертати з кутовою швидкістю
. Крайні точки фазних обмоток називають «початками» А, В, С і, відповідно, «кінцями». X, Y, Z. Всередині статора розташований ротор на обмотки якого подається постійний струм і таким чином створюється магнітне поле. Якщо ротор обертати з кутовою швидкістю 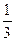 періоду обертання від попередньої.
періоду обертання від попередньої.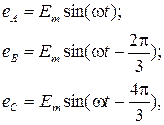 або
або 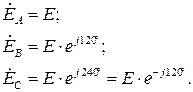

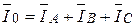 . В симетричній трифазній системі напруг живлення та при рівномірному навантаженні фаз струм в нейтральному проводі дорівнює нулю. В несиметричній системі величина струму в нейтральному проводі розраховується символічним методом або графічним, як векторна сума фазних струмів.
. В симетричній трифазній системі напруг живлення та при рівномірному навантаженні фаз струм в нейтральному проводі дорівнює нулю. В несиметричній системі величина струму в нейтральному проводі розраховується символічним методом або графічним, як векторна сума фазних струмів.
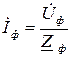 , де
, де 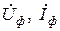 комплекси діючих значень фазної напруги та відповідної їй фазного струму, а
комплекси діючих значень фазної напруги та відповідної їй фазного струму, а  – загальний опір споживача записаний в комплексній формі.
– загальний опір споживача записаний в комплексній формі.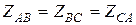 то і струми в фазах будуть рівними по величині
то і струми в фазах будуть рівними по величині 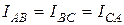 але зсунуті між собою на кут
але зсунуті між собою на кут 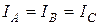 і їх величина більша від величини фазних струмів на
і їх величина більша від величини фазних струмів на  ,тобто
,тобто  .
.
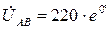 В, то комплексні значення інших фазних напруг буде відповідно дорівнювати
В, то комплексні значення інших фазних напруг буде відповідно дорівнювати  а
а 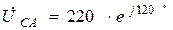 . Загальні опори фаз згідно рис.2.10 та заданих значень різні і в комплексній формі записуються так:
. Загальні опори фаз згідно рис.2.10 та заданих значень різні і в комплексній формі записуються так: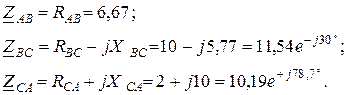
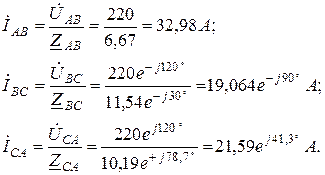
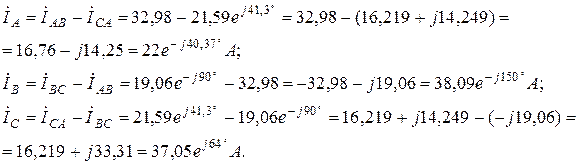 Ррозрахунок потужностей фаз трифазного споживача та всього трифазного несиметричного кола зручно виконувати символічним методом.
Ррозрахунок потужностей фаз трифазного споживача та всього трифазного несиметричного кола зручно виконувати символічним методом. , де
, де  – спряжений фазовий струм в комплексній формі запису.
– спряжений фазовий струм в комплексній формі запису.