
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Табличные значения производных основных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. (un)' = n × un-1 × u' (n Î R) 2. (au)' = au × lna× u' 3. (eu)' = eu × u' 4.(log a u)' = 5. (ln u)' = 6. (sin u)' = cos u × u' 7. (cos u)' = - sin u× u' 8. (tg u)' = 9. (ctg u)' = - 10. (arcsin u)' = 11. (arccos u)' = - 12. (arctg u)' = 13. (arcctg u)' = - Пример. Вычислить производную функции: у = Для нахождения данной производной сначала преобразуем заданную функцию: у = у ′ = Пример. Вычислить производную функции: у = Данная производная вычисляется по 4 правилу дифференцирования (u =2 x 2+3, v =7 x 2+2): у′ = = Пример. Найти производную функции у = е 3-4 х Данная функция является сложной. Обозначим u = 3 - 4 х, тогда у = еu. Далее воспользовавшись 3 табличным значением производной, получим: у ′ = (eu)' = eu × u' = е 3-4 х ∙ (3 - 4 х)′ = е 3-4 х ∙ (-4) = - 4 е 3-4 х
Пример. Вычислить производную функции: у = (5 х 2+3 х -7)6 Данная функция является сложной. Обозначим u = 5 х 2+3 х -7, получим функцию у = u6, для нахождения производной которой воспользуемся 1 табличным значением: у ′ = 6 u 5 = 6∙(5 х 2+3 х -7)5 ∙ (5 х 2+3 х -7)′ = 6∙(5 х 2+3 х -7)5 ∙ (10 x +3)
Практическое занятие №13 Наименование занятия: Приложение дифференциала к приближенным вычислениям Цель занятия: Научиться находить дифференциал функции, вычислять приближенные значения функции, приращения функции с помощью дифференциала Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной» Литература:
Задание на занятие: 1. Найти дифференциалы следующих функций: 1) 2) 3) 4) 5) 2. Найти приближенное значение приращения функции 3. На сколько приближенно изменится значение степени 25, если основание увеличится на 0,003? 4. Сторона квадратного листа жести, равная 15 см, после нагревания увеличилась на 0,001 см. Вычислите приближенно, на сколько изменилась площадь этого листа.
1) 2)
1) (1,025)10 2) 3) е -0,005 4) 22,98 5) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Дифференциалом функции f(x) в точке х 0 называется линейная относительно D x функция
Пример. Найти дифференциал функции Сначала преобразуем данную функцию:
Тогда дифференциал будет равен
Приближенные вычисления с помощью дифференциала 1. Вычисление приближенного значения приращения функции:
Пример. Пользуясь понятием дифференциала функции, вычислить приближенно изменение функции Найдем дифференциал функции
2. Вычисление приближенного значения функции: Пример. Вычислить приближенное значение с помощью дифференциала 1,9985. Рассмотрим функцию Найдем значение Тогда 1,9985» 32 – 0,16 = 31, 84.
Практическое занятие №14 Наименование занятия: Нахождение производных высших порядков. Правила Лопиталя. Цель занятия: Научиться находить производные высших порядков, применять правило Лопиталя к вычислению пределов. Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной» Литература:
Задание на занятие:
1. Найти производные 2-го следующих функций. 1) 2) 3) 4) 5)
2. Дана функция 3. Вычислить производные 3-го порядка следующих функций. 1) 2) 4. Дана функция
3. Вычислить пределы, используя правило Лопиталя. 1) 2) 3) 4) 5)
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Производные высших порядков Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную Если найти производную функции f¢(x), получим вторую производную функции f(x):
Этот процесс можно продолжить и далее, находя производные степени n:
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.155 (0.008 с.) |

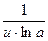 × u'
× u'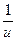 × u '
× u '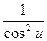 × u'
× u'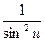 × u'
× u'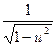 × u'
× u'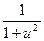 × u'
× u'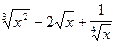
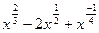 . Далее воспользуемся 1 табличным значением:
. Далее воспользуемся 1 табличным значением: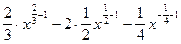 =
= 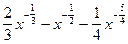 =
= 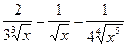
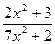
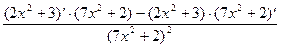 =
= 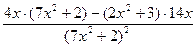 =
=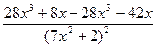 = -
= - 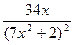
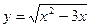
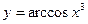

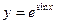
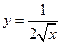 в точке х = 1.
в точке х = 1.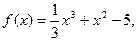 при изменении аргумента от х = 3 до х = 3,1
при изменении аргумента от х = 3 до х = 3,1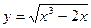 в точке х = 1,96
в точке х = 1,96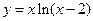 в точке х =3,012
в точке х =3,012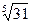
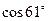
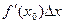 , составляющая главную часть приращения функции в точке х 0. Обозначается df (х 0) или dy. Вычисляется по формуле: dy = f¢(x)dx.
, составляющая главную часть приращения функции в точке х 0. Обозначается df (х 0) или dy. Вычисляется по формуле: dy = f¢(x)dx.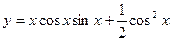 .
.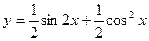 , найдем производную
, найдем производную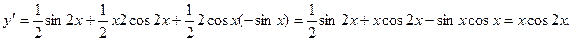
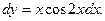
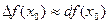
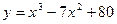 при изменении аргумента от 5 до 5,01.
при изменении аргумента от 5 до 5,01.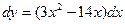 . Подставим значения х 0 = 5, D х = 0,01. Получим
. Подставим значения х 0 = 5, D х = 0,01. Получим 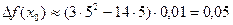
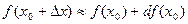
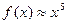 , где х = 1,998. Разобьем х на х 0 и D х (х = х 0 + D х), пусть х 0 = 2, тогда D х = - 0,002.
, где х = 1,998. Разобьем х на х 0 и D х (х = х 0 + D х), пусть х 0 = 2, тогда D х = - 0,002.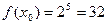 ,
, 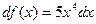 ,
, 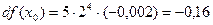
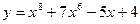 ;
;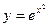 ;
; ;
;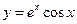 ;
;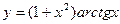 .
.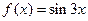 . Найти
. Найти 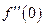 ,
, 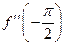 ,
, 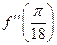 .
. ;
;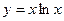
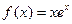 . Найти
. Найти 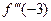 ,
, 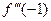 ,
, 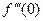 .
.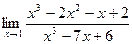 ;
;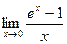 ;
;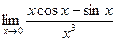 ;
;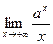 ;
;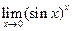 .
.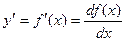
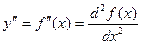 , т.е. y¢¢ = (y¢)¢ или
, т.е. y¢¢ = (y¢)¢ или 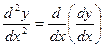 .
.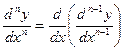 .
.


