
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы неопределенностей и методы их раскрытияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей. I. Неопределенность вида Пример. Вычислить предел При подстановке вместо переменной х числа - 2 видим, что получается неопределенность вида Пример. Вычислить предел При подстановке х =0 получается неопределенность вида Умножим числитель и знаменатель дроби на сопряженное числителю выражение:
II. Неопределенность вида Для раскрытия этой неопределенности нужно каждое слагаемое числителя и знаменателя разделить на переменную в наибольшей степени и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность. Пример. Вычислить предел Здесь числитель и знаменатель не имеют предела, т.к. оба неограниченно возрастают. В этом случае имеем неопределенность вида
Величины
Пример. Вычислить предел Имеем неопределенность вида
Замечательные пределы Первый замечательный предел: Следствия: 1) Второй замечательный предел: Следствие: Третий замечательный предел: Четвертый замечательный предел: Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов. Пример. Вычислить предел
Сравнение бесконечно малых функций Пусть a(х) и b(х) бесконечно малые функции при х ® А. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю. Например, функция f(x) = x 10 стремится к нулю быстрее, чем функция f(x) = x. Бесконечно малые функции a(х) и b(х) при х ® А называются эквивалентными бесконечно малыми, если При х ®0 эквивалентными бесконечно малыми являются следующие функции: 1. sin x ~ х; 2. tg x ~ x; 3. ln(1+ x) ~ x; 4. ex – 1 ~ x; 5. 1 – cos x ~ 6. ax – 1 ~ x ln a; 7. (1 + x) a – 1 ~ ax; 8. arcsin x ~ x; 9. arctg x ~ x.
Пример. Найти предел Так как tg5 x ~ 5 x и sin7 x ~ 7 x при х® 0, то, заменив функции эквивалентными бесконечно малыми, получим: Пример. Найти предел Так как 1 – cos x = Практическое занятие №11 Наименование занятия: Вычисление односторонних пределов, классификация точек разрыва. Цель занятия: Научиться вычислять односторонние пределы, находить точки разрыва, определять их тип. Подготовка к занятию: Повторить теоретический материал по теме «Теория пределов. Непрерывность» Литература:
Задание на занятие: 1. Вычислить односторонние пределы: 1) 2)
2. Вычислить односторонние пределы при 1) 2)
у = 0 при х < 0; у = х при 0 ≤ х < 1; у = - х2 + 4 х -2 при 1 ≤ х < 3; у = 4 – х при x > 3. Будет ли эта функция непрерывной? Построить график.
4. Найти точки разрыва функций и определить их тип: 1) 2) 3) 4)
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Если f(x) ® b при х ® а только при x < a, то Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы b 1 и b 2 называются также односторонними пределами функции f(x) в точке х=а. Функция f(x) называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е. Если функция f(x) определена в некоторой окрестности точки х 0, но не является непрерывной в самой точке х 0, то она называется разрывной функцией, а точка х 0 – точкой разрыва функции.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.007 с.) |

 .
.


 =
=  .
. .
.
 =
=  =
= 
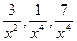 являются бесконечно малыми при
являются бесконечно малыми при  и их пределы равны нулю. Следовательно, искомый предел равен
и их пределы равны нулю. Следовательно, искомый предел равен 


 ; 2)
; 2)  ; 3)
; 3)  .
.

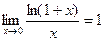
 при
при  ,
,  .
.
 . Записывают a(х) ~ b(х).
. Записывают a(х) ~ b(х). ;
;

 .
.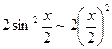 при х ®0, то
при х ®0, то  .
.

 следующих функций:
следующих функций:

 3. Функция определена следующим образом:
3. Функция определена следующим образом:
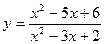



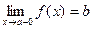 - называется левым пределом функции f(x) в точке х = а, а если f(x) ® b при х ® а только при x > a, то
- называется левым пределом функции f(x) в точке х = а, а если f(x) ® b при х ® а только при x > a, то  называется правым пределом функции f(x) в точке х = а.
называется правым пределом функции f(x) в точке х = а.



