
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрытие неопределенностей. Правило ЛопиталяСодержание книги
Поиск на нашем сайте
Теорема Лопиталя. Если функции f(x) и g(x) дифференцируемы в окрестности точки а, непрерывны в точке а, g¢(x) отлична от нуля в окрестности точки а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
Замечание. Теорема остается в силе и в том случае, когда в точке x = a функции j (x) и y (x) обращаются в бесконечность. Правило Лопиталя. Для раскрытия неопределенностей Пример: Найти предел При попытке непосредственного вычисления предела получается неопределенность вида
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя. Пример: Найти предел При подстановке х = 0 получается неопределенность вида
Для раскрытия других неопределенностей Пример Неопределенности вида
Пример: Найти предел Здесь y = xx, ln y = x ln x. Тогда Следовательно
Практическое занятие №15 Наименование занятия: Нахождение точек перегиба и направлений выпуклости, асимптот графика функции Цель занятия: Научиться исследовать функции на выпуклость, вогнутость, находить асимптоты графика функции
Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной» Литература:
Задание на занятие: 1. Исследовать функции на выпуклость, вогнутость. Найти точки перегиба. 1) 2) 3) 4) 5)
2. Найти асимптоты графиков функций: 1) 2) 3) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
График функции f(x) называется выпуклым на интервале (a; b), если он расположен ниже касательной, проведенной к любой его точке. График функции f(x) называется вогнутым на интервале (a; b), если он расположен выше касательной, проведенной к любой его точке. Теорема (достаточное условие выпуклости, вогнутости графика функции). Если функция y = f(x) имеет на интервале (a; b) вторую производную f′′(x) и она положительна, то функция вогнута на этом интервале. Если же f′′(x) отрицательна на интервале (a; b), то функция выпукла на этом интервале. Точка графика функции при переходе через которую кривая меняет направление выпуклости, называется точкой перегиба. Теорема (достаточное условие существования точки перегиба) Если функция y = f(x) имеет на интервале (a; b) вторую производную f′′(x) и при переходе через точку х = x0 f¢¢(x) меняет знак, то точка кривой с абсциссой х = x0 является точкой перегиба. Асимптотой кривой называется прямая, к которой неограниченно приближается график функции. Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные. Вертикальные асимптоты. Если Например, для функции Наклонные асимптоты. Наклонная асимптота задается уравнением y = kx + b. Для точного определения этой прямой необходимо найти коэффициенты k и b. Они находятся следующим образом: Горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0. Пример. Найти асимптоты функции Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой, т.к. в этих точках функция имеет разрыв 2-го рода. Найдем наклонные асимптоты:
Практическое занятие №16 Наименование занятия: Полное исследование функций. Построение графиков. Цель занятия: Научиться исследовать функции и по результатам исследования строить графики. Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной» Литература:
Задание на занятие: 1. Исследовать функции по общей схеме и построить графики.
1) 2) 3) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Схема исследования функций
1. Найти область определения функции и определить точки разрыва, если они имеются. 2. Установить, является функция четной или нечетной или ни той ни другой. Если функция четна или нечетна, то достаточно рассмотреть ее значения при x>0, а затем симметрично относительно оси OY или начала координат восстановить ее и для значений x<0. 3. Исследовать функцию на периодичность. Если функция периодическая, то достаточно рассмотреть ее на одном периоде. 4. Найти точки пересечения графика функции с осями координат (если это возможно) 5. Провести исследование функции на экстремум и найти интервалы возрастания и убывания функции. 6. Найти точки перегиба кривой и интервалы выпуклости, вогнутости функции. 7. Найти асимптоты графика функции. 8. Пользуясь результатами шагов 1-7, строят график функции. Иногда для большей точности находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой. Пример. Исследовать функцию 1) Областью определения функции являются промежутки (-¥; -1) È (-1; 1) È (1; ¥). Областью значенийданной функции является интервал (-¥; ¥). Точками разрыва функции являются точки х = 1, х = -1. 2) Функция является нечетной, т.к. 3) Функция не периодическая. 4) График пересекает оси координат в точке (0; 0).
5) Находим критические точки.
Критические точки: x = 0; x = - Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках. -¥ < x < - - -1 < x < 0, y ¢ < 0, функция убывает 0 < x < 1, y ¢ < 0, функция убывает 1 < x <
Видно, что точка х = -
6) Найдем вторую производную функции
Определим выпуклость и вогнутость кривой на промежутках. -¥ < x < - - -1 < x < 0, y ¢¢ > 0, кривая вогнутая 0 < x < 1, y ¢¢ < 0, кривая выпуклая 1 < x <
7) Найдем асимптоты кривой. Прямые х = 1, х = -1 являются вертикальными асимптотами, т.к. в них односторонние пределы равны бесконечности. Теперь найдем наклонные асимптоты.
Уравнение наклонной асимптоты: y = x.
8) Построим график функции по результатам исследования.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.63.222 (0.007 с.) |


 и
и  надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций.
надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций. .
.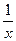 ; g¢(x) = ex. Тогда
; g¢(x) = ex. Тогда  .
.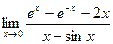 .
. ;
;  и подставим их в предел:
и подставим их в предел:  - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз.  ;
;  ;
; - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз. ;
;  ;
;  .
. ,
,  ,
,  ,
,  их следует предварительно преобразовать к неопределенности вида
их следует предварительно преобразовать к неопределенности вида 
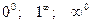 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида  , f(x)> 0 в окрестности точки а при х® а. Для нахождения предела такой функции достаточно найти предел функции ln y = g(x) ln f(x).
, f(x)> 0 в окрестности точки а при х® а. Для нахождения предела такой функции достаточно найти предел функции ln y = g(x) ln f(x). .
.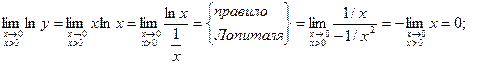 .
.


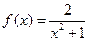





 ,
,  , или
, или 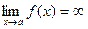 , то прямая х = а является вертикальной асимптотой кривой y = f(x). Вертикальные асимптоты обычно сопровождают точки разрыва второго рода и если функция непрерывна, то вертикальных асимптот нет.
, то прямая х = а является вертикальной асимптотой кривой y = f(x). Вертикальные асимптоты обычно сопровождают точки разрыва второго рода и если функция непрерывна, то вертикальных асимптот нет. прямая х = 5 является вертикальной асимптотой.
прямая х = 5 является вертикальной асимптотой. ,
, 
 .
.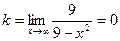 , следовательно, наклонной асимптоты функция не имеет. Найдем
, следовательно, наклонной асимптоты функция не имеет. Найдем  , т.е. y = 0 – горизонтальная асимптота.
, т.е. y = 0 – горизонтальная асимптота.


 и построить ее график.
и построить ее график. .
.
 ; x =
; x = 


 .
.





