
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Крамера для решения систем линейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Это решение может быть найдено по формулам
Пример. Решить систему уравнений методом Крамера: D = D1 = D2 = D3 = x 1 =
Практическое занятие №4 Наименование занятия: Решение систем линейных уравнений методом Гаусса Цель занятия: Научиться решать системы линейных уравнений методом Гаусса Подготовка к занятию: Повторить теоретический материал по теме «Системы линейных уравнений» Литература:
Задание на занятие:
1)
2)
4)
5)
3)
6) Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ Рассмотрим произвольную систему линейных уравнений. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решением системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Для этой системы линейных уравнений вида матрица
А =
А*= Метод Гаусса Суть метода заключается в том, что систему уравнений с помощью элементарных преобразований приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называются прямым ходом. Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход). Элементарными преобразованиями систем являются: 1) Умножение или деление коэффициентов и свободных членов на одно и то же число 2) Сложение и вычитание уравнений 3) Перестановка уравнений системы местами. 4) Исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю Пример. Решить систему линейных уравнений методом Гаусса Составим расширенную матрицу системы. А* = Выполним над этой матрицей следующие преобразования: 1) поменяем местами 1 и 2 строки; 2) прибавим к элементам 2 строки 1-ю строку, умноженную на -2; 3) прибавим к элементам 3 строки 1-ю строку, умноженную на -7; 4) прибавим к элементам 3 строки 2-ю строку, умноженную на -3; А* = Получили систему с треугольной матрицей. Таким образом, исходная система может быть представлена в виде:
Практическое занятие №5 Наименование занятия: Операции над векторами Цель занятия: Научиться выполнять действия с векторами Подготовка к занятию: Повторить теоретический материал по теме «Векторы. Операции над векторами» Литература:
Задание на занятие:
Порядок проведения занятия:
Содержание отчета:
Контрольные вопросы для зачета:
ПРИЛОЖЕНИЕ
Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевойвектор – это вектор, начало и конец которого совпадают. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
Действия над векторами 1. Суммой двух векторов называется вектор 2. Произведением вектора 1) 2) вектор 3) вектор Координаты вектора Пусть точки А(х 1, y 1) и B(x 2, y 2), заданы в прямоугольной декартовой системе координат. Чтобы найти координаты вектора
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 698; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.190.117 (0.008 с.) |

 , где
, где  - определитель системы
- определитель системы ,
,  , …,
, …, 

 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30; = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30. = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90. = 1; x 2 =
= 1; x 2 =  = 2; x 3 =
= 2; x 3 =  = 3.
= 3.





 ,
, называется матрицей системы, а матрица
называется матрицей системы, а матрица называется расширенной матрицей системы
называется расширенной матрицей системы
 .
.
 , откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1.
, откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1. и
и  . Построить векторы
. Построить векторы  ,
,  .
. ,
,  ,
,  , если А (2; 3), В (-1; -3), С (-7; 5).
, если А (2; 3), В (-1; -3), С (-7; 5). ,
,  ,
,  ,
, 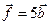 .
. .
.
 совпадет с началом вектора
совпадет с началом вектора  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: ;
; нужно из координат его конца вычесть координаты начала т.е.
нужно из координат его конца вычесть координаты начала т.е. 


