
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В линейных, параметрических и нелинейных ФУСодержание книги
Поиск на нашем сайте
Линейные преобразования сигналов и ФУ Линейные ФУ по определению описываются линейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей) с постоянными коэффициентами. С точки зрения схемотехники это значит, что все элементы ФУ (R, C, L) имеют постоянные параметры. Оператором преобразования воздействия x (t) в реакцию y (t) для них может служить одна из форм интеграла наложения (Дюамеля) во временной области
или передаточная функция Н
а в качестве функциональной характеристики линейного ФУ можно использовать его импульсную характеристику Простым колебанием для линейных цепей является гармоническое 1. Форма сложного сигнала (с полигармоническим или сплошным спектром) при его прохождении через линейную цепь может изменяться только вследствие изменения соотношения между амплитудами и фазами спектральных составляющих воздействия. Принципиально важно, что в реакции линейного ФУ не могут возникнуть спектральные компоненты, отсутствующие в спектре воздействия. 2. Из вывода 1 вытекают возможности построения на основе линейных цепей ограниченного класса типовых ФУ: а) усилителей и аттенюаторов (ФУ для изменения мощности сигналов без искажения их формы), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид
б) фильтров разных типов (ФНЧ, ФВЧ, ПФ, РФ, интеграторов, дифференциаторов, фазовращателей и т.п.), передаточная функция которых в полосе частот, занимаемой спектром воздействия, имеет вид
где Н (w) (АЧХ) и j(w) (ФЧХ) – заданные функции частоты. Параметрические преобразования сигналов и ФУ По определению параметрические ФУ описываются линейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей), у которых есть коэффициенты, зависящие от независимой переменной (времени).
где Рассмотрим реакцию параметрического звена (рис. 3.1) при
Спектры воздействия и реакции приведены на рис. 3.3. Из их рассмотрения можно сделать следующие выводы: 1. Параметрические ФУ обогащают спектр воздействия новыми спектральными составляющими. 2. Частоты новых спектральных составляющих в реакции параметрических ФУ определяются частотами спектральных составляющих воздействия и частотами изменения параметров ФУ.
Нелинейные преобразования сигналов и ФУ Нелинейные преобразователи сигналов описываются нелинейными дифференциальными уравнениями (в том числе нулевого порядка для резистивных цепей), у которых хотя бы один коэффициент зависит от их решения (искомой функции). Соответственно, их схема содержит хотя бы один
нелинейный элемент, параметр(ы) которого зависит от протекающего тока или приложенного напряжения.
Рассмотрим возможности изменения спектра сигнала при его прохождении через БНП – цепь 0-го порядка. Для таких цепей в теории широко используют два основных метода спектрального анализа реакции в зависимости от вида аппроксимации функциональной характеристики БНП:
1) метод кратных дуг – при полиномиальной аппроксимации
2) метод угла отсечки (коэффициентов Берга) – при кусочно-линейной аппроксимации. Чтобы воспользоваться первым методом, достаточно помнить тригонометрическую формулу
и её частный случай (при
Результаты анализа спектрального состава реакции БНП с полиномиальной функциональной характеристикой при моно- и бигармоническом воздействии приведены в таблице 3.1. В ней указаны только частоты спектральных составляющих реакции. Из этой таблицы следует, что БНП обогащает спектр воздействия постоянной составляющей, кратными гармониками и колебаниями комбинационных частот вида Выводы 1. Нелинейные ФУ обогащают спектр воздействия новыми спектральными компонентами. 2. Новые спектральные компоненты реакции нелинейных ФУ являются гармониками частот воздействия или колебаниями комбинационных частот вида
Таблица 3.1
Контрольные вопросы 1. Сформулируйте задачи анализа и синтеза ФУ. 2. Дайте классификацию ФУ по виду описывающих их дифференциальных уравнений. 3. Каковы принципиальные ограничения на возможности преобразования сигналов в линейных ФУ? 4. Что можно использовать в качестве функциональных характеристик линейных ФУ? 5. Какие типовые ФУ, используемые в системах связи, можно реализовать в классе линейных цепей? 6. Каковы возможности параметрических ФУ по преобразованию сигналов? 7. Опишите характер обогащения спектров сигналов в параметрических ФУ. 8. Каковы возможности нелинейных ФУ по преобразованию сигналов? 9. Какие виды аппроксимации функциональных характеристик безынерционных нелинейных преобразователей целесообразны в режимах а) слабого сигнала, б) сильного сигнала?
10. Какой метод спектрального анализа реакции нелинейного ФУ используют при аппроксимации его функциональной характеристики степенным полиномом? 11. Какой метод спектрального анализа реакции нелинейного ФУ используют при кусочно-линейной аппроксимации его функциональной характеристики? 12. Опишите спектральный состав реакции нелинейного ФУ на моногармоническое воздействие. 13. Опишите спектральный состав реакции нелинейного ФУ на полигармоническое воздействие. 14. Нарисуйте схему перемножителя сигналов и укажите назначение её элементов. 15. При каких условиях кольцевой диодный перемножитель обеспечивает «чистое» перемножение сигналов? 16. В чём сущность метода фазовой компенсации побочных продуктов нелинейного преобразования сигналов?
Рекомендации по проведению экспериментальных исследований преобразований сигналов в линейных, нелинейных и параметрических ФУ Для закрепления полученных в разделе 3.1 знаний полезно выполнить лабораторные работы № 2 «Линейная фильтрация сигналов» (рис. 3.5), № 6 «Преобразования сигналов в нелинейных цепях» (рис. 3.6) и № 7 «Нелинейное усиление и умножение частоты сигналов» (из перечня тем виртуальной учебной лаборатории) (рис. 3.7) в полных объёмах, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите, прежде всего, внимание на принципиальные различия в характере трансформации спектров входных сигналов в результате их линейных и нелинейных преобразований. Сформулируйте, в чём состоят эти отличия и какие практически важные следствия они имеют с точки зрения реализации ФУ раз-
личного назначения. Обратите внимание на функции нелинейного элемента и его линейной нагрузки в нелинейных преобразователях и конкретизируйте из применительно к нелинейному усилителю и умножителю частоты сигналов. Для экспериментальных исследований параметрических преобразований сигналов можно воспользоваться параметрическими преобразователями, входящими в состав системы передачи непрерывных сообщений из лабораторной работы № 11 «Линейные виды модуляции и синхронное детектирование» (рис. 3.8). В рамках ресурсов, предоставляемых этой работой, можно провести наблюдение осциллограмм и спектрограмм произведения произвольного сигнала s 1(t) с гармоническим колебанием. В качестве произвольного входного сигнала s 1(t) используйте как НЧ, так и ВЧ сигналы, выбирая их с помощью пункта меню «Сигналы/ s 1(t)» этой работы. Обратите внимание на характер обогащения спектра параметрическим преобразователем и определите частоты новых спектральных составляющих на его выходе. Перемножение сигналов
1) все диоды имеют квадратичные вольтамперные характеристики (режим слабого сигнала)
с одинаковыми коэффициентами 2) сопротивления нагрузочных резисторов R одинаковы (симметрия схемы), 3) один из входных сигналов поступает от двух идентичных источников (e 1) (симметрия схемы). Выходное напряжение
Для определения токов диодов подставим в выражение их вольтамперной характеристики соответствующие напряжения
+ – –
Обратим внимание на то, что Выводы 1. ФУ (рис. 3.10) является «чистым» перемножителем произвольных сигналов 2. «Чистота» операции перемножения достигнута методом фазовой компенсации. 3. Суть метода фазовой компенсации заключается в следующем: · ФУ строится по симметричной многоканальной схеме, · выходные реакции каналов суммируются, · на входы каналов сигналы подают с таким подбором фаз, чтобы при сложении реакций каналов полезные составляющие оказались бы синфазными и суммировались, а побочные были бы противофазными и взаимно компенсировались.
Амплитудная модуляция Модуляция в системах связи используется тогда, когда непосредственная передача первичного сигнала по линии связи оказывается невозможной. Согласование передаваемого сигнала с характеристиками линии связи достигается использованием колебания, которое хорошо распространяется в имеющейся линии связи. Один или несколько параметров этого колебания связывают с первичным сигналом. Такое колебание называют переносчиком, процесс изменения его параметра(ов) – модуляцией, первичный сигнал – модулирующим, а получаемый вторичный сигнал – модулированным. В качестве переносчика широко применяют гармоническое несущее колебание
Добавление к модулирующему сигналу
Спектры АМ сигналов Спектр простого АМ сигнала. Модулированный сигнал называют простым, если в качестве модулирующего сигнала
где U н – амплитуда несущего колебания, m – коэффициент (глубина) модуляции, Для получения спектра сигнала простого АМ сигнала достаточно в выражении (3.2) раскрыть скобки
Таким образом, спектр простого АМ сигнала содержит несущее и два боковых колебания (рис.3.11). Нетрудно видеть, что его ширина
Спектр сложного АМ сигнала На основе выражения (3.2) спектр сложного АМ сигнала при полигармоническом модулирующем сигнале можно записать в виде
где W1, W2,… – частоты модулирующего сигнала, m 1, m 2,… – парциальные коэффициенты модуляции. В случае Т -финитного модулирующего сигнала соответствующий АМ сигнал выглядит следующим образом
где k АМ – нормирующий коэффициент, обеспечивающий условие A (t)≥0. Для нахождения его спектральной функции перейдём к комплексному сигналу
Используя свойства преобразования Фурье (2.6) и (2.7), получим
Выводы 1. Спектр АМ сигнала содержит: а) несущее колебание на частоте wн, б) верхнюю боковую полосу (ВБП), представляющую собой спектр модулирующего сигнала в) нижнюю боковую полосу (НБП), являющуюся «зеркальным отражением» ВБП относительно wн. 2. Ширина спектра АМ сигнала вдвое больше максимальной модулирующей частоты Энергетика АМ сигналов Определим мощность простого АМ сигнала, понимая под ней среднее за период несущего колебания значение квадрата сигнала (3.2)
где Максимальная (пиковая) мощность, на которую рассчитывают усилители АМ сигналов,
до 4 раз превышает мощность Средняя мощность АМ сигнала за период модулирующего сигнала (потребляемая от источников питания модулятора или усилителя АМ сигнала)
где Из полученных результатов можно сделать вывод о низкой энергетической эффективности амплитудной модуляции, так как полезная (в информационном смысле) мощность боковых колебаний
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.127 (0.01 с.) |

 ,
, ФУ в частотной области
ФУ в частотной области ,
, или передаточную функцию Н
или передаточную функцию Н  . Его форма не изменяется при прохождении через любую линейную цепь. В линейных цепях действует принцип суперпозиции – реакция цепи на сумму воздействий есть сумма её реакций на каждое из воздействий в отдельности. Из этих свойств вытекают следующие выводы:
. Его форма не изменяется при прохождении через любую линейную цепь. В линейных цепях действует принцип суперпозиции – реакция цепи на сумму воздействий есть сумма её реакций на каждое из воздействий в отдельности. Из этих свойств вытекают следующие выводы: , где Н 0 и t0 – константы;
, где Н 0 и t0 – константы;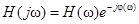 ,
,






 Схемотехнически это означает, что параметрический ФУ содержит хотя бы один элемент, параметр(ы) которого зависит от времени. В подавляющем большинстве случаев параметрические ФУ строятся на использовании перемножителя сигналов (рис. 3.2). Действительно, если генератор колебания
Схемотехнически это означает, что параметрический ФУ содержит хотя бы один элемент, параметр(ы) которого зависит от времени. В подавляющем большинстве случаев параметрические ФУ строятся на использовании перемножителя сигналов (рис. 3.2). Действительно, если генератор колебания  рассматривать как внутренний элемент ФУ («чёрного ящика»), то
рассматривать как внутренний элемент ФУ («чёрного ящика»), то  можно записать в виде
можно записать в виде ,
, (коэффициент передачи параметрического звена) может служить его функциональной характеристикой.
(коэффициент передачи параметрического звена) может служить его функциональной характеристикой. на воздействие вида
на воздействие вида  .
.
 .
.





 Спектр
Спектр 
 0 wс w
Спектр
0 wс w
Спектр 
 0 W w
Спектр
0 W w
Спектр  0 W wс–W wс wс+W w
Рис.3.3. Спектры
0 W wс–W wс wс+W w
Рис.3.3. Спектры 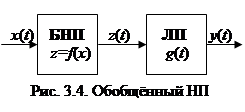

 Анализ нелинейных ФУ в общем случае является сложной задачей, которая существенно упрощается, если возможно разделить ФУ на две независимые части, сосредоточив всю нелинейность в безынерционном нелинейном преобразователе (БНП) а всю инерционность – в линейном (ЛП), как это показано на рис. 3.4. Назовём такую структуру обобщённым нелинейным преобразователем (ОНП). Для анализа ОНП достаточно по известной функциональной характеристике БНП
Анализ нелинейных ФУ в общем случае является сложной задачей, которая существенно упрощается, если возможно разделить ФУ на две независимые части, сосредоточив всю нелинейность в безынерционном нелинейном преобразователе (БНП) а всю инерционность – в линейном (ЛП), как это показано на рис. 3.4. Назовём такую структуру обобщённым нелинейным преобразователем (ОНП). Для анализа ОНП достаточно по известной функциональной характеристике БНП 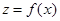 (для безынерционной цепи это обычная функция, а не оператор) определить его реакцию
(для безынерционной цепи это обычная функция, а не оператор) определить его реакцию  на заданное воздействие
на заданное воздействие  ,
,
 )
) .
. , где
, где  ,
,  , причём порядок комбинационных частот
, причём порядок комбинационных частот  (не превосходит степени n полинома, аппроксимирующего функциональную характеристику БНП). Этот вывод можно распространить и на случай полигармонического воздействия.
(не превосходит степени n полинома, аппроксимирующего функциональную характеристику БНП). Этот вывод можно распространить и на случай полигармонического воздействия.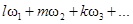 , где l,m,k= 0, ±1, ±2,…
, где l,m,k= 0, ±1, ±2,…




 ,
, 
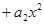
 ,
, 

 , 3w0
, 3w0
 ,
,  ,
,  ,
,  ,
,  ,
, 

 ,
,
 ,
,
 ,
,

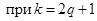 , q = 1, 2, 3,…
, q = 1, 2, 3,…

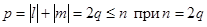 ,
,

 q = 1, 2, 3,…
q = 1, 2, 3,…









 В качестве первого типового ФУ рассмотрим перемножитель сигналов, тем более, что он используется в параметрическом звене (рис. 3.1). По определению перемножителем является ФУ с двумя входами, выходной сигнал которого пропорционален произведению входных сигналов (рис.3.9). Поскольку операция перемножения не является линейной, то схемотехническое решение перемножителя следует искать в классе нелинейных цепей.
В качестве первого типового ФУ рассмотрим перемножитель сигналов, тем более, что он используется в параметрическом звене (рис. 3.1). По определению перемножителем является ФУ с двумя входами, выходной сигнал которого пропорционален произведению входных сигналов (рис.3.9). Поскольку операция перемножения не является линейной, то схемотехническое решение перемножителя следует искать в классе нелинейных цепей.



























 Проанализируем схему кольцевого (мостового) перемножителя (рис. 3.10), в которой в качестве нелинейных элементов используются диоды. Предварительно сделаем следующие допущения:
Проанализируем схему кольцевого (мостового) перемножителя (рис. 3.10), в которой в качестве нелинейных элементов используются диоды. Предварительно сделаем следующие допущения:
 ,
,
 .
. , определяя последние через входные сигналы
, определяя последние через входные сигналы  и
и 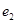 . Падением напряжения на нагрузке при этом будем пренебрегать. Произведём алгебраическое суммирование токов:
. Падением напряжения на нагрузке при этом будем пренебрегать. Произведём алгебраическое суммирование токов:


 +
+ 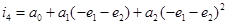
 .
. и
и 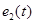 (в рамках выше сделанных допущений о режиме слабого сигнала, симметрии схемы, идентичности характеристик диодов).
(в рамках выше сделанных допущений о режиме слабого сигнала, симметрии схемы, идентичности характеристик диодов). , обладающее тремя параметрами: амплитудой А, частотой w и начальной фазой j. Соответственно возможны три простых вида модуляции: амплитудная, частотная и фазовая. При амплитудной модуляции первичный сигнал
, обладающее тремя параметрами: амплитудой А, частотой w и начальной фазой j. Соответственно возможны три простых вида модуляции: амплитудная, частотная и фазовая. При амплитудной модуляции первичный сигнал  отображают в амплитуде (огибающей) А несущего колебания следующим образом
отображают в амплитуде (огибающей) А несущего колебания следующим образом . (3.1)
. (3.1) необходимо, чтобы сделать эту сумму униполярной, т.к. огибающая
необходимо, чтобы сделать эту сумму униполярной, т.к. огибающая 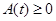 по определению. Разумеется, если модулирующий сигнал сам по себе является униполярным, например, сигнал изображения в телевидении, то никакой добавки не требуется (
по определению. Разумеется, если модулирующий сигнал сам по себе является униполярным, например, сигнал изображения в телевидении, то никакой добавки не требуется ( ).
).
 , (3.2)
, (3.2)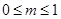 .
.
 .
. , где
, где  – частота модулирующего сигнала. Обратите внимание на то, что амплитуда несущего колебания не зависит от модулирующего сигнала в отличие от амплитуд боковых колебаний. Это говорит о том, что информации о модулирующем сигнале в несущем колебании не содержится. Она содержится исключительно в боковых колебаниях, которые возникают в процессе осуществления амплитудной модуляции.
– частота модулирующего сигнала. Обратите внимание на то, что амплитуда несущего колебания не зависит от модулирующего сигнала в отличие от амплитуд боковых колебаний. Это говорит о том, что информации о модулирующем сигнале в несущем колебании не содержится. Она содержится исключительно в боковых колебаниях, которые возникают в процессе осуществления амплитудной модуляции.





 Спектры:
Спектры:
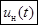



 0 W w
0 W w

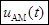

 ,
, 
 , (3.3)
, (3.3)
 ,
, .
. . (3.4)
. (3.4)



























 Спектры сигналов (3.3) и (3.4) приведены на рис.3.12.
Спектры сигналов (3.3) и (3.4) приведены на рис.3.12.
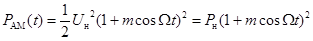 ,
, – мощность несущего колебания.
– мощность несущего колебания. ,
, ,
, – мощность боковых колебаний.
– мощность боковых колебаний. не превышает половины от мощности несущего колебаний
не превышает половины от мощности несущего колебаний  .
.


