
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о системах связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Министерство Российской Федерации По связи и информатизации
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ Им. проф. М.А.Бонч-Бруевича
А.П. Сальников
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Конспект лекций Часть 1
САНКТ-ПЕТЕРБУРГ
УДК 621.391.1
Сальников А.П. Теория электрической связи: Конспект лекций, часть 1/ СПбГУТ. –СПб., 2002. –93 с.: ил.
Предназначено для студентов, изучающих дисциплину «Теория электрической связи». Содержит общие сведения о системах связи, описание моделей детерминированных сигналов. Рассмотрены преобразования сигналов в типовых функциональных узлах систем связи (модуляторах и детекторах разных видов, перемножителях и преобразователях частоты сигналов). Приведены контрольные вопросы по всем разделам для самопроверки их усвоения и рекомендации по проведению сопутствующих экспериментальных исследований в виртуальной учебной лаборатории по курсу ТЭС. Материал соответствует действующей учебной программе по курсу ТЭС.
Ответственный редактор М.Н. Чесноков
© Сальников А.П., 2002 © Издание Санкт-Петербургского государственного университета телекоммуникаций им. проф. М.А. Бонч-Бруевича, 2002
Редактор И.И. Щенсняк
ЛР № от.02. Подписано к печати.02 Объем 8,125 уч.-изд. л. Тир. 200 экз. Зак.
РИО СПбГУТ. 191186, СПб., наб. р. Мойки, 61 Общие сведения о системах связи Информация, сообщения, сигналы Под информацией понимают совокупность каких-либо сведений о явлениях, объектах и т.п. Сообщения представляют собой материальную форму существования информации и могут иметь различную физическую природу. Сигналами в электрической связи служат процессы (функции времени) электрической природы, посредством которых осуществляется передача сообщений на расстояние. Общее и различное в этих основополагающих понятиях теории связи поясняется таблицей 1.1. В ней также указаны возможные преобразователи сообщений в сигналы, которые называют датчиками сигналов. Таблица 1.1.
Текстовые сообщения представляют собой последовательности символов из некоторого конечного множества { a i } (языка) с известным объемом алфавита m. Преобразование такого рода сообщений в сигнал может осуществляться, например, клавиатурой ЭВМ путем поочередного кодирования отдельных символов сообщения k -разрядными комбинациями из 0 и 1, которым соответствуют два разных уровня напряжения. Звуковые сообщения представляют собой изменения давления воздушной среды в заданной точке пространства во времени p (t). С помощью микрофона они преобразуются в переменный электрический сигнал u (t), который в определенном смысле является копией сообщения и отличается от него лишь физической размерностью. Видеосообщения можно рассматривать как распределение яркости на поверхности объекта b (x,y), неподвижное изображение которого требуется передать на расстояние (фототелеграф), или более сложный процесс b (x,y,t) (черно-белое телевидение). Характерной особенностью при передаче видеосообщений является необходимость преобразования описывающих их многомерных функций в одномерный сигнал u (t). Это достигается использованием в датчиках видеосигналов устройств развертки (УР) для поэлементного преобразования яркости отдельных точек объектов в уровень электрического сигнала с помощью фотоэлементов (ФЭ) или иных фотоэлектрических преобразователей.
Классификация сигналов По относительной ширине спектра сигналы делят на низкочастотные (называемые также НЧ, видео, широкополосные сигналы) и высокочастотные (ВЧ, радио, узкополосные, полосовые сигналы).
Для НЧ сигналов Δ F / F ср> 1, где Δ F = F max– F min– абсолютная ширина спектра сигнала, F ср= (F max+ F min)/2 – средняя частота спектра сигнала, F max– максимальная частота в спектре сигнала, F min– минимальная частота в спектре сигнала. Для ВЧ сигналов Δ F / F ср << 1. Как правило, первичные сигналы на выходе датчиков являются низкочастотными. Полезно помнить диапазоны частот, в которых располагаются спектры типичных сигналов в системах связи и вещания:
1) телефонный – 300 ÷ 3400 Гц (стандартный канал тональной частоты), 2) радиовещательный – от 30–50 Гц до 6–15 кГц, 3) телевизионный – 0 ÷ 6 МГц (для вещательного стандарта разложения изображения, принятого в России). По своей природе различают сигналы детерминированные и случайные. Детерминированные сигналы считаются известными в каждой точке временной оси. В отличие от них значения случайных (стохастических) сигналов в каждый момент времени являются случайной величиной с той или иной вероятностью. Очевидно, что детерминированные сигналы в силу своей полной определенности не могут нести никакой информации. Их удобно использовать в теории для анализа различных функциональных узлов (ФУ), а на практике в качестве испытательных сигналов для измерения неизвестных параметров и характеристик отдельных звеньев трактов систем связи. По форме сигналы можно разделить на четыре вида, приведенные в таблице 1.2.
Таблица 1.2.
Сигнал (1), непрерывный по времени и состояниям, называют аналоговым. Сигнал (4), дискретный по времени и состояниям, – цифровым. Эти сигналы чаще всего используются в различных узлах систем связи. Соответственно различают аналоговые и цифровые ФУ по форме сигналов на их входах и выходах. Возможны преобразования аналогового сигнала в цифровой с помощью аналого-цифрового преобразователя (АЦП) и, наоборот, – с помощью цифро-аналогового преобразователя (ЦАП). Условные графические обозначения (УГО) этих типовых ФУ приведены на рис. 1.1.
Сигналы можно рассматривать в качестве объектов транспортировки по каналам связи и характеризовать основными параметрами, такими как - длительность сигнала Т с, - ширина его спектра F c, - динамический диапазон
мгновенные мощности сигнала.
Пользуются также более общей характеристикой – объемом сигнала
Классификация систем связи По виду передаваемых сообщений различают: 1) телеграфию (передача текста), 2) телефонию (передача речи), 3) фототелеграфию (передача неподвижных изображений), 4) телевидение (передача подвижных изображений), 5) телеметрию (передача результатов измерений), 6) телеуправление (передача управляющих команд), 7) передачу данных (в вычислительных системах и АСУ). По диапазону частот – в соответствии с декадным делением диапазонов электромагнитных волн от мириаметровых (3÷30) кГц до децимиллиметровых (300÷3000) ГГц. По назначению – вещательные (высококачественная передача речи, музыки, видео от малого числа источников сообщений большому количеству их получателей) и профессиональные (связные), в которых число источников и получателей сообщений одного порядка. Различают следующие режимы работы СС: 1) симплексный (передача сигналов в одном направлении), 2) дуплексный (одновременная передача сигналов в прямом и обратном направлениях), 3) полудуплексный (поочередная передача сигналов в прямом и обратном направлениях).
Уточним уже использованный нами термин канал связи. Под ним принято понимать часть СС между точками А на передающей и Б на приемной сторонах. В зависимости от выбора этих точек, иначе говоря, по виду сигналов на входе и выходе различают каналы: 1) непрерывные, 2) дискретные, 3) дискретно-непрерывные, 4) непрерывно-дискретные. Каналы связи можно характеризовать по аналогии с сигналами следующими тремя параметрами: – временем доступа – шириной полосы пропускания – динамическим диапазоном где сигнала в канале,
Обобщенным параметром канала является его емкость
Очевидным необходимым условием согласования сигнала и канала является выполнение неравенства V c < V к. Менее очевидно то, что это условие является также достаточным и вовсе не обязательно добиваться аналогичного согласования по частным параметрам (длительности, спектру, динамическому диапазону), так как возможен «обмен» ширины спектра сигнала на его длительность или динамический диапазон. Контрольные вопросы 1. Дайте определения понятиям информация, сообщение сигнал. Какие между ними связи и различия? 2. Приведите примеры сообщений разной физической природы и соответствующих им датчиков сигналов. 3. Каким образом сообщения, описываемые многомерными функциями, преобразуются в сигналы? Приведите примеры. 4. Классифицируйте сигналы по особенностям их формы и спектра. 5. По какому признаку различают НЧ и ВЧ сигналы? 6. По какому критерию различают аналоговые и цифровые сигналы и ФУ? 7. Укажите основные параметры сигналов. 8. Нарисуйте структурные схемы систем связи для: · передачи дискретных сообщений, · передачи непрерывных сообщений, · передачи непрерывных сообщения по цифровым каналам. 9. Укажите назначение следующих ФУ систем связи: · кодера источника и кодера канала, · модулятора, · демодулятора, · декодера канала и декодера источника. 10. Что общего и различного в задачах, решаемых демодуляторами СПДС и СПНС? 11. Какие системы связи Вам известны: · по виду передаваемых сообщений, · по диапазону используемых частот, · по назначению, · по режимам работы? 12. Дайте определение термину «канал связи». Какая классификация каналов связи Вам известна? 13. Укажите основные параметры каналов связи. 14. Сформулируйте условия согласования сигналов и каналов связи.
Рекомендации по проведению экспериментальных исследований сигналов в системах связи
Для закрепления полученных в разделах 1.1 и 1.2. знаний полезно выполнить лабораторную работу № 14 «Знакомство с системами ПДС» (из перечня тем виртуальной учебной лаборатории) в полном объёме. Эта работа носит ознакомительный характер и позволяет наблюдать все основные процессы получения, преобразования и приёма сигналов в системах передачи дискретных сообщений (рис. 1.3). Следует обратить внимание на осциллограммы и спектрограммы сигналов на выходах типовых ФУ (кодера источника при выборе разных типов интерфейса, кодера канала при выборе разных помехоустойчивых кодов, модулятора при разных видах модуляции, демодулятора и декодера), входящих в системы ПДС, и сопоставить с ними свои представления, полученные в ходе изучения раздела. Рекомендуется по результатам наблюдения сигналов в разных точках тракта СПДС провести их классификацию, определить их основные параметры, а также выделить в СПДС разные типы каналов (непрерывный, дискретный, дискретно-непрерывный и непрерывно-дискретный). Полезно также получение наглядного представления о функции каждого ФУ СПДС. Для закрепления полученных сведений о различии НЧ и ВЧ сигналов и наполнения их практическим содержанием целесообразно провести исследования в рамках лабораторной работы № 4 «Модулированные сигналы». Выбирая в качестве первичных НЧ сигналы разных форм, обратите внимание не только на различие осциллограмм и спектрограмм первичных (НЧ) и модулированных (ВЧ) сигналов, но и на объединяющие их признаки при использовании разных видов модуляции (рис. 1.4). При выполнении указанных работ не обязательно строго придерживаться имеющихся в них заданий. Используйте возможности ресурсов ВЛ для проведения исследований по своему усмотрению и желанию.
Пространств Сигналы – это, прежде всего, процессы, т.е. функции времени x (t), существующие на ограниченном интервале Т (в теории возможно Т → ∞). Их можно изобразить графически (рис. 2.1) и описывать упорядоченной последовательностью значений в отдельные моменты времени tk
В математике под пространством понимают множество объектов (любой физической природы), наделенных некоторым общим свойством. Свойства, которыми целесообразно наделять пространства сигналов, должны отражать наиболее существенные свойства реальных сигналов, такие как их длительность, энергия, мощность и т.п.
Метрические пространства Первое свойство, которым мы наделим пространство сигналов, называют метрикой. Метрическое пространство – это множество с подходящим образом определенным расстоянием между его элементами. Само это расстояние, как и способ его определения, называют метрикой и обозначают
1) 2) 3)
Следует отметить, что метрики можно задать разными способами и в результате для одних и тех же элементов получить разные пространства.
Примеры метрик: 1) 2) 3) Линейные пространства Усовершенствуем структуру пространства сигналов, наделив его простыми алгебраическими свойствами, присущими реальным сигналам, которые можно алгебраически складывать и умножать на числа. Линейным пространством L над полем F называют множество элементов 1. Замкнутость операций сложения и умножения на скаляр:
2. Свойства сложения:
3. Свойства умножения на скаляр:
4. 5. воположного вектора.
Вектор, образованный суммированием нескольких векторов со скалярными коэффициентами
называют линейной комбинацией (многообразием). Легко видеть, что множество всех линейных комбинаций векторов Множество векторов называют линейно независимыми, если равенство
возможно лишь при всех a i = 0. Например, на плоскости любые два неколлинеарные вектора (не лежащие на одной прямой) являются линейно независимыми. Система линейно независимых и ненулевых векторов
Этот единственный набор скаляров {a i }, соответствующий конкретному вектору Благодаря введению базиса операции над векторами превращаются в операции над числами (координатами)
Если в линейном пространстве L можно отыскать n линейно независимых векторов, а любые n + 1 векторов зависимы, то n – размерность пространства L (dim L = n).
Нормированные пространства Следующий наш шаг в совершенствовании структуры пространства сигналов – объединение геометрических (характерных для метрических пространств) и алгебраических (для линейных пространств) свойств путем введения действительного числа, характеризующего «размер» элемента в пространстве. Такое число называют нормой вектора и обозначают В качестве нормы можно использовать любое отображение линейного пространства на действительную ось, удовлетворяющее следующим аксиомам: 1) 2) 3) Выводы 1. Математическим аппаратом спектрального анализа периодических сигналов являются ряды Фурье. 2. Спектры периодических сигналов дискретные (линейчатые), представляют собой совокупность амплитуд и фаз гармонических колебаний (составляющих) следующих по оси частот через интервалы Δ f = f 1 = 1/ T. 3. Ряд Фурье является частным случаем обобщенного ряда Фурье при использовании в качестве базиса
Спектры Т-финитных сигналов Т-финитными называют ограниченные по времени сигналы. По определению они не могут быть периодическими и, следовательно, к ним не применимо разложение в ряды Фурье. Чтобы получить адекватное описание таких сигналов в частотной области используют следующий прием. На первом этапе от заданного сигнала x (t), имеющего начало в точке t 1 и конец в точке t 2 переходят к сигналу x п(t), являющемуся периодическим повторением x (t) на бесконечной оси времени с периодом где Введём в рассмотрение текущую частоту Тогда Исходный сигнал x (t) можно получить из x п(t) в результате предельного перехода Т® ¥. При этом
В данном случае (и в дальнейшем) комплексную функцию Из полученных соотношений следует, что спектр Т-фи- нитного сигнала сплошной. Он представляет собой совокупность бесконечного числа спектральных составляющих с бесконечно малыми амплитудами
где
Выводы 1. Математическим аппаратом спектрального анализа Т-финитных сигналов является интегральное преобразование Фурье. 2. Спектры Т-финитных сигналов сплошные и описываются непрерывными функциями частоты в виде модуля спектральной плотности амплитуд
Свойства преобразования Фурье 1. Прямое и обратное преобразование Фурье являются линейными операторами, следовательно, действует принцип суперпозиции. Если 2. Прямое и обратное преобразование Фурье являются взаимно однозначными. 3. Свойство запаздывания. Если
(в данном случае использованы подстановки: 4. Спектральная функция δ-функции. Используя общее выражение спектральной функции и фильтрующее свойство δ-функции, получим
5. Спектральная функция комплексного гармонического сигнала
Используя одно из определений δ-функции и выполняя в нём взаимную замену t и w (или f), получим
Сопоставляя полученный результат с (2.5), имеем
6. Скалярное произведение комплексных сигналов в спектральной области. Пусть
Из полученного результата для вещественных функций
где а Для сигналов x (t), заданных на бесконечной оси времени (–¥,+¥), с
Тогда
7. Скалярное произведение комплексных сигналов При
– корреляционная функция сигнала x (t). Из последнего выражения вытекают важные соотношения между корреляционной функцией и энергетическим спектром сигнала
8. Спектр произведения сигналов
Таким образом, спектральная функция произведения двух сигналов является свёрткой их спектральных функций. Справедливо также и обратное соотношение
9. Свойство смещения спектра. Если
10. Ширина спектра. Теоретически ширина спектра сигналов бесконечна. Однако, учитывая, что интенсивность спектральных составляющих реальных сигналов уменьшается с ростом их частоты (не обязательно монотонно), можно ввести понятие практической (конечной) ширины спектров (рис. 2.3 и 2.4). Практическую ширину спектра DW можно определять как ширину частотного интервала, в пределах которого амплитудный спектр S(w) не меньше некоторого условного уровня g (например g = 0,1) от S(w)max или энергия (мощность) сигнала составляет определённую часть g (например g = 0,9) от полной
Для импульсов простых форм (прямоугольной, треугольной и т.п.), спектральная функция которых периодически принимает нулевые значения с ростом частоты (рис. 2.3 и 2.4), практическую ширину спектра часто определяют по первому или второму или иному «нулю» амплитудного спектра. Независимо от способа определения практической ширины спектра Т-финитного сигнала выполняется общая закономерность – произведение практической ширины спектра на длительность сигнала D t есть константа C, зависящая только от формы импульса DW·D t = C. Это соотношение имеет фундаментальное значение в теории связи. Из него вытекает, что чем короче сигнал, тем шире его спектр и, следовательно, тем более широкополосный канал требуется для его передачи.
Контрольные вопросы 1. Какие сигналы являются периодическими? 2. Какой математический аппарат используется для спектрального анализа периодических сигналов? 3. Что называют амплитудным и фазовым спектрами периодического сигнала? 4. Какими свойствами обладают спектры периодических сигналов? 5. Как вычисляют амплитуды и фазы спектральных составляющих периодических сигналов? 6. Какие сигналы называют Т -финитными? 7. Какой математический аппарат используется для спектрального анализа Т -финитных сигналов? 8. Что такое спектральная функция (спектральная плотность амплитуд) сигнала и какова её размерность? 9. Что понимают под амплитудным и фазовым спектрами Т -финитного сигнала? 10. Как изменяется спектр сигнала в результате его задержки на время t? 11. Что представляет собой спектр d-функции? 12. Какова спектральная функция гармонического колебания? 13. Как можно вычислить скалярное произведение сигналов в спектральной области? 14. Что представляют собой спектральные плотности энергии и мощности сигналов? Каковы их размерности и свойства? 15. Что представляет собой корреляционная функция сигнала 16. Как вычисляют спектр произведения сигналов? 17. Как изменяется спектр сигнала в результате его умножения на гармоническое колебание?
Рекомендации по проведению экспериментальных исследований ортогональности и спектров сигналов Для закрепления полученных в разделе 2.1 знаний полезно провести экспериментальные исследования на базе лабораторной работы № 5 «Ортогональность сигналов» (из перечня тем виртуальной учебной лаборатории) в полном объёме (рис. 2.2). Она позволяет понять, как на практике реализуется вычисление скалярного произведения двух сигналов, экспериментально определить являются ли выбранные пары сигналов ортогональными на установленном временном интервале. Обратите внимание на условия ортогональности двух гармонических сигналов разных частот и их связь с интервалом ортогональности. Для закрепления полученных в разделе 2.3 знаний по спектральному представлению периодических сигналов полезно выполнить лабораторную работу № 1 «Сигналы и спектры» в полном объёме, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этой работы ресурсов (рис. 2.3). Обратите внимание на дискретность спектров и связи их характеристик с параметрами и формой сигналов. Для закрепления полученных в разделе 2.3 знаний по спектральному представлению финитных сигналов полезно на базе лабораторной работы № 22 «Согласованная фильтрация сигналов известной формы» провести экспериментальные исследования спектров одиночных импульсов разных форм, используя генератор сигналов, предоставляемый этой работой (рис. 2.4). Обратите внимание на сплошной характер спектров одино
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 929; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.5.179 (0.012 с.) |




 Текст
Текст
 Звук
Звук
 Факс
Видео
Факс
Видео
















 Значения u (t)
Значения u (t)

 u (t)
u (t)
 t
t
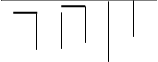





 , где
, где и
и 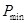 – максимальная и минимальная
– максимальная и минимальная .На интуитивном уровне очевидно, чем больше объем сигнала, тем он информативнее, но тем и выше требования к качеству канала для его передачи.
.На интуитивном уровне очевидно, чем больше объем сигнала, тем он информативнее, но тем и выше требования к качеству канала для его передачи. ,
, ,
,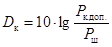 [дБ],
[дБ], – максимально допустимая мощность
– максимально допустимая мощность – мощность собственных шумов канала.
– мощность собственных шумов канала.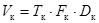 .
.

 (вектор строка).
(вектор строка). Разные сигналы отличаются формой (набором значений x (tk)). Вместо сложной совокупности точек кривой x (t) в простой области – двумерном пространстве можно ввести в рассмотрение более сложные пространства (пространства сигналов), в которых каждый сигнал изображается простейшим элементом – точкой (вектором).
Разные сигналы отличаются формой (набором значений x (tk)). Вместо сложной совокупности точек кривой x (t) в простой области – двумерном пространстве можно ввести в рассмотрение более сложные пространства (пространства сигналов), в которых каждый сигнал изображается простейшим элементом – точкой (вектором). . Метрика должна представлять собой функционал, т.е. отображение любой пары элементов
. Метрика должна представлять собой функционал, т.е. отображение любой пары элементов  и
и 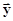 множества на действительную ось, удовлетворяющее интуитивно понятным требованиям (аксиомам):
множества на действительную ось, удовлетворяющее интуитивно понятным требованиям (аксиомам): (равенство при
(равенство при 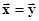 ),
),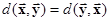 ,
, (аксиома треугольника).
(аксиома треугольника). ,
, евклидова метрика,
евклидова метрика,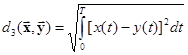 евклидова метрика.
евклидова метрика. , называемых векторами, для которых заданы две операции –сложение элементов (векторов)
, называемых векторами, для которых заданы две операции –сложение элементов (векторов)  и умножение векторов на элементы из поля F (называемые скалярами)
и умножение векторов на элементы из поля F (называемые скалярами)  . Не вдаваясь в математические детали, в дальнейшем, под полем скаляров будем понимать множества вещественных чисел R (случай действительного пространства L) или комплексных чисел С (случай комплексного пространства L). Эти операции должны удовлетворять системе аксиом линейного пространства.
. Не вдаваясь в математические детали, в дальнейшем, под полем скаляров будем понимать множества вещественных чисел R (случай действительного пространства L) или комплексных чисел С (случай комплексного пространства L). Эти операции должны удовлетворять системе аксиом линейного пространства.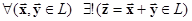 ,
, .
. ассоциативность,
ассоциативность, коммутативность.
коммутативность. ассоциативность,
ассоциативность,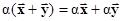 дистрибутивность суммы векторов,
дистрибутивность суммы векторов, дистрибутивность суммы скаляров.
дистрибутивность суммы скаляров. существование нулевого вектора.
существование нулевого вектора. существование проти-
существование проти- ,
,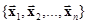 при разных a i (не затрагивая
при разных a i (не затрагивая  ) также образует линейное пространство, называемое линейной оболочкой для векторов
) также образует линейное пространство, называемое линейной оболочкой для векторов 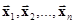 .
.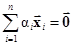
 образует в пространстве L базис, если
образует в пространстве L базис, если .
. .
. .
.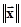 .
. ,
,  = 0,
= 0,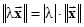 ,
,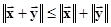 .
. или
или  .
. . Сигнал x п(t) можно разложить в ряд Фурье
. Сигнал x п(t) можно разложить в ряд Фурье ,
, .
. и спектральную плотность амплитуд
и спектральную плотность амплитуд  .
. .
. ,
, 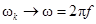 , å ® ò,
, å ® ò, 
 ,
,
 Таким образом, для описания спектра финитного сигнала приходим к известному в математике интегральному преобразованию Фурье:
Таким образом, для описания спектра финитного сигнала приходим к известному в математике интегральному преобразованию Фурье: – прямое,
– прямое, – обратное.
– обратное. 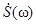 записали в виде
записали в виде  , как это принято в научно-технической литературе.
, как это принято в научно-технической литературе. , непрерывно следующих по оси часты. Вместо этих бесконечно малых амплитуд используют спектральную функцию (спектральную плотность амплитуд)
, непрерывно следующих по оси часты. Вместо этих бесконечно малых амплитуд используют спектральную функцию (спектральную плотность амплитуд) ,
, – амплитудный спектр,
– амплитудный спектр,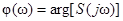 – фазовый спектр.
– фазовый спектр. (амплитудный спектр) и её аргумента
(амплитудный спектр) и её аргумента  , то
, то 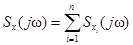 .
. , то
, то
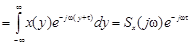


 ).
). .
.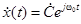 .
.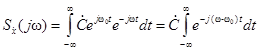 (2.5)
(2.5)
 и
и  .
. (2.6)
(2.6) и
и 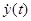 – комплексные функции на интервале (–T/2, T/2). Их скалярное произведение
– комплексные функции на интервале (–T/2, T/2). Их скалярное произведение

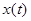 вытекает равенство Парсеваля (обобщённая формула Рэлея)
вытекает равенство Парсеваля (обобщённая формула Рэлея)
 ,
, – энергия сигнала
– энергия сигнала  – спектральная плотность энергии.
– спектральная плотность энергии. , но имеющих ограниченную мощность
, но имеющих ограниченную мощность  , вместо спектральной плотности энергии
, вместо спектральной плотности энергии 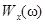 можно использовать спектральную плотность мощности (энергетический спектр)
можно использовать спектральную плотность мощности (энергетический спектр) .
. , т.к.
, т.к. и
и  – чётные функции,
– чётные функции,  – односторонняя спектральная плотность мощности (энергетический спектр).
– односторонняя спектральная плотность мощности (энергетический спектр). в спектральной области.
в спектральной области. 
 .
. и
и 

 ,
,  –
–
 ,
, .
. .
.
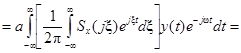

 ,
,  – – свертка функций
– – свертка функций  и
и  .
. .
. , то
, то 
 . (2.7)
. (2.7) .
. ?
?


