
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторная диаграмма колебания с УМСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Из аналитического выражения колебания с УМ (3.8) видно, что его амплитуда U 0 сохраняется неизменной, следовательно, вектор комплексной амплитуды плоскости (рис. 3.35). Годограф этого вектора представляет собой окружность.
где М – максимальное отклонение фазы от среднего значения называют индексом модуляции. Изменение мгновенной частоты простого колебания с УМ происходит по закону
где
Для определения спектра простого колебания с УМ удобно перейти к его комплексному сигналу
Из теории функций Бесселя известно, что
где Jk (M) – функции Бесселя первого рода порядка k от аргумента М (k = 0, ±1, ±2,…). Они обладают свойством
Рис. 3.36. Графики функций Бесселя Подставляя (3.10) в (3.9), получаем
Вернёмся к действительному сигналу
Спектр простого сигнала с УМ, соответствующий полученному выражению, приведён на рис. 3.37.
Для определения ширины спектра простого сигнала с
Таким образом, при М >> 1
и можно считать, что ширина спектра простого колебания с УМ вдвое больше его девиации частоты и существенно больше (в М раз) ширины спектра АМ сигнала. При М << 1 достаточно в спектре этого колебания удержать первую пару боковых и считать его ширину
равной ширине спектра простого АМ сигнала. Методы осуществления угловой модуляции Различают два основных метода осуществления угловой модуляции – прямой и косвенный. По прямому методу реализуют частотные модуляторы на основе генераторов, частота колебаний которых управляется внешним напряжением (ГУН) (рис. 3.38). Особенностью ГУН является включение в его колебательную систему, от собственной частоты w0 которой зависит частота wг генерируемых колебаний, уп-равляемого реактивного элемента (УРЭ). В качестве УРЭ можно использовать варикап, «реактивный транзистор», ёмкость (индуктивность) которых зависит от приложенного напряжения (протекающего тока). Достоинством прямого метода является возможность
По косвенному методу реализуют фазовые модуляторы на основе схемы, представленной на рис. 3.39. Выясним условия, при которых эта схема обеспечивает ФМ. На выходе сумматора имеем
При выполнении условия
Таким образом установили, что рассмотренная схема может служить фазовым модулятором только при выполнении указанного неравенства, иначе говоря, только при малом индексе модуляции (М <<1) выходного сигнала u ФМ(t). Это её основной недостаток, а достоинством является высокая стабильность несущей частоты u ФМ(t) при использовании высокостабильного генератора несущего колебания. Детектирование сигналов с угловой модуляцией
Детектирование ФМ сигналов Для детектирования ФМ сигналов можно использовать ранее рассмотренный синхронный детектор (рис. 3.27). При
Детектирование ЧМ сигналов Для построения частотных детекторов используются два метода связанные с преобразованием вида модуляции: 1) преобразование ЧМ в АМ с последующим амплитудным детектированием, 2) преобразование ЧМ в ФМ с последующим фазовым детектированием Первый метод реализован в схеме частотного детектора с расстроенными контурами (рис. 3.41). Преобразователь ЧМ в АМ выполнен на двух колебательных контурах, расстроенных относительно частоты сигнала
где U с – амплитуда входного сигнала m - коэффициент передачи входного трансформатора,
1-го контура,
2-го контура.
Выводы 1. Частотный детектор с расстроенными контурами работает по методу преобразования ЧМ в АМ с последующим амплитудным детектированием. 2. Достоинством данного частотного детектора является возможность достижения высокой крутизны его ХД. 3. Основной недостаток – сложность настройки. От неё зависит степень линейности рабочего участка ХД. 4. Частотный детектор (рис. 3.41) целесообразно использовать при приёме сигналов с цифровой ЧМ, когда важна крутизна ХД, а степень её линейности роли не играет.
где g - коэффициент пропорциональности, Dj – фазовый сдвиг между
где М – взаимная индуктивность между L 1и L 2,
r – сопротивление потерь контура, Q – добротность контура,
где
1) 2) arctgx, 3) sin(arctgx).
Рис. 3.44. Характеристика детектирования частотного дискриминатора
Выводы 1. Частотный дискриминатор реализует метод преобразования ЧМ в ФМ с последующим фазовым детектированием. 2. Частотный дискриминатор прост в настройке, т.к. его контур настраивается на частоту сигнала 3. Обеспечивается высокая степень линейности рабочего участка ХД вне зависимости от настройки контура. 4. Частотный дискриминатор целесообразно применять при приёме сигналов с аналоговой ЧМ, когда важна линейность ХД. Контрольные вопросы 1. Дайте определения видам модуляции: угловая, фазовая, частотная. 2. Каким образом можно с помощью фазового модулятора получить ЧМ сигнал? 3. Каким образом можно с помощью частотного модулятора получить ФМ сигнал? 4. Что представляет собой векторная диаграмма колебания с угловой модуляцией? 5. Дайте определения индексу модуляции и девиации частоты. Какая между ними связь? 6. Какой спектр имеет простое колебание с УМ? 7. Как определяют практическую ширину спектра ФМ и ЧМ сигналов? 8. Нарисуйте схему фазового детектора. Какой вид имеет его ХД? 9. Какие методы используются при построении частотных детекторов? 10. Нарисуйте схему частотного детектора с расстроенными контурами. 11. Напишите аналитическое выражение ХД частотного детектора с расстроенными контурами, нарисуйте и объясните её форму. 12. Нарисуйте схему частотного дискриминатора. 13. Напишите аналитическое выражение и нарисуйте форму ХД частотного дискриминатора. 14. Проведите сравнительный анализ частотных детекторов разных типов. Рекомендации по проведению экспериментальных исследований ФМ и ЧМ сигналов и фазового детектора Для закрепления полученных в разделе 3.7 знаний полезно выполнить лабораторную работу № 4 «Модулированный сигналы» (из перечня тем виртуальной учебной лаборатории) в части исследования сигналов с фазовой и частотной модуляцией (рис. 3.45), а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите внимание на общее и разное в ЧМ и ФМ сигналах при одном и том же модулирующем сигнале (особенно при использовании в качестве модулирующего сигнала гармонического колебания и импульсов треугольной формы). Убедитесь в расширении спектра ФМ и ЧМ сигналов с увеличением индекса модуляции, определите для каждого случая их практическую ширину. Для закрепления полученных в разделе 3.8 знаний рекомендуется выполнить лабораторную работу № 13 «Детектирование ФМ сигналов» (рис. 3.46) в полном объёме, а также провести дополнительные экспериментальные исследования, используя иные виды сигналов в рамках предоставляемых этими работами ресурсов. Обратите внимание на вид экспериментально получаемой характеристики детектирования фазового детектора и на влияние выбора протяжённости её рабочего участка на степень искажений выходного сигнала.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.008 с.) |

 не изменяет свою длину и может только вращаться на комплексной
не изменяет свою длину и может только вращаться на комплексной
























 ,
, ,
, (
( ) – девиация частоты.
) – девиация частоты. Спектр простого колебания с УМ
Спектр простого колебания с УМ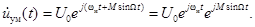 (3.9)
(3.9) , (3.10)
, (3.10) .
. Графики функций Бесселя приведены на рис. 3.36.
Графики функций Бесселя приведены на рис. 3.36. .
. .
.









 УМ учтём ещё одно свойство функций Бесселя – с ростом их порядка увеличивается начальная область значений аргумента М, при которых модуль этих функций очень мал. Обычно, пренебрегают боковыми компонентами с номерами k > M +1, считая практическую ширину спектра
УМ учтём ещё одно свойство функций Бесселя – с ростом их порядка увеличивается начальная область значений аргумента М, при которых модуль этих функций очень мал. Обычно, пренебрегают боковыми компонентами с номерами k > M +1, считая практическую ширину спектра .
.




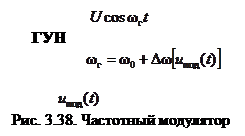 получения большой девиации частоты (М >>1), т.е. широкополосной частотной модуляции, а основным недостатком – трудность обеспечения высокой стабильности несущей частоты.
получения большой девиации частоты (М >>1), т.е. широкополосной частотной модуляции, а основным недостатком – трудность обеспечения высокой стабильности несущей частоты.










 =
=
 .
.
 .
. в качестве опорного колебания используют
в качестве опорного колебания используют  . Это позволяет получить характеристику детектирования
. Это позволяет получить характеристику детектирования  в виде
в виде , (3.11)
, (3.11)


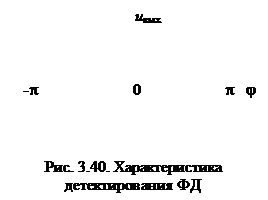 где {…}НЧ обозначает низкочастотную часть выражения в фигурных скобках (после прохождения через ФНЧ). График характеристики детектирования фазового детектора приведён на рис. 3.40.
где {…}НЧ обозначает низкочастотную часть выражения в фигурных скобках (после прохождения через ФНЧ). График характеристики детектирования фазового детектора приведён на рис. 3.40. и
и  , где Dwр (расстройка) выбирается таким образом, чтобы получить максимальную линейность рабочего участка характеристики детектирования. Амплитудные детекторы выполнены по выше рассмотренной схеме диодного детектора огибающей (рис. 3.24).
, где Dwр (расстройка) выбирается таким образом, чтобы получить максимальную линейность рабочего участка характеристики детектирования. Амплитудные детекторы выполнены по выше рассмотренной схеме диодного детектора огибающей (рис. 3.24).
















 Вычислим характеристику детектирования (ХД)
Вычислим характеристику детектирования (ХД)  , где
, где  – частота входного гармонического сигнала.
– частота входного гармонического сигнала. , (3.12)
, (3.12) ,
, – обобщённая расстройка
– обобщённая расстройка – обобщённая расстройка
– обобщённая расстройка
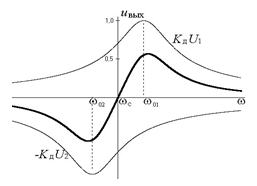 На рис. 3.42 утолщённой линией приведён график ХД, соответствующий выражению (3.12). Относительно линейная часть ХД используется в качестве её рабочей области. Нетрудно видеть, что требуется тщательное симметрирование схемы (Q 1 = Q 2 = Q) и настройка контуров на частоты
На рис. 3.42 утолщённой линией приведён график ХД, соответствующий выражению (3.12). Относительно линейная часть ХД используется в качестве её рабочей области. Нетрудно видеть, что требуется тщательное симметрирование схемы (Q 1 = Q 2 = Q) и настройка контуров на частоты  , правильный выбор которых зависит от добротности Q. Сложность настройки – главный недостаток данного частотного детектора, а к его достоинствам можно отнести возможность получения высокой крутизны ХД при Q >> 1.
, правильный выбор которых зависит от добротности Q. Сложность настройки – главный недостаток данного частотного детектора, а к его достоинствам можно отнести возможность получения высокой крутизны ХД при Q >> 1.













































 Преобразование ЧМ в ФМ с последующим фазовым детектированием используется в частотном дискриминаторе, схема которого приведена на рис. 3.43. В этой схеме преобразование ЧМ сигнала u 1(t) в ФМ сигнал u 2(t) осуществляется колебательным контуром L2 C2, настроенным на частоту сигнала
Преобразование ЧМ в ФМ с последующим фазовым детектированием используется в частотном дискриминаторе, схема которого приведена на рис. 3.43. В этой схеме преобразование ЧМ сигнала u 1(t) в ФМ сигнал u 2(t) осуществляется колебательным контуром L2 C2, настроенным на частоту сигнала  а фазовый детектор (ФД) выполнен по балансной схеме, содержащей перемножитель напряжений
а фазовый детектор (ФД) выполнен по балансной схеме, содержащей перемножитель напряжений  и
и  на диодах VD1, VD2 и ФНЧ 1-го порядка (RC нагрузка). Вспомогательные элементы разделительный конденсатор С р и дроссель L др служат для подачи входного напряжения
на диодах VD1, VD2 и ФНЧ 1-го порядка (RC нагрузка). Вспомогательные элементы разделительный конденсатор С р и дроссель L др служат для подачи входного напряжения  в качестве опорного на второй вход перемножителя. Определим ХД частотного дискриминатора – зависимость его выходного напряженияот частоты
в качестве опорного на второй вход перемножителя. Определим ХД частотного дискриминатора – зависимость его выходного напряженияот частоты  входного гармонического сигнала
входного гармонического сигнала  . Учитывая (3.11), имеем
. Учитывая (3.11), имеем  ,
, = const,
= const, .
. ,
,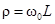 – характеристическое сопротивление контура,
– характеристическое сопротивление контура, – обобщённая расстройка.
– обобщённая расстройка. .
.  .
.
 , (3.13)
, (3.13) .
. На рис. 3.44 приведён график ХД (кривая 4), построенный по выражению (3.13), а также ряд вспомогательных кривых:
На рис. 3.44 приведён график ХД (кривая 4), построенный по выражению (3.13), а также ряд вспомогательных кривых: ,
,




