
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крутильные колебания роторов гтдСодержание книги
Поиск на нашем сайте
Элементы ротора ГТД: диски компрессоров, газовых турбин, шестерни редукторов, воздушные винты и т.д., соединенные валами образуют упругую систему, которая под действием изменяющегося крутящего момента может совершать крутильные колебания (колебания в окружном направлении). При крутильных колебаниях массы системы находящиеся во вращательном движении поворачиваются относительно друг друга на угол
Рис.4.1. Схема турбовинтового двигателя с моментами инерции
Источником крутильных колебаний в ГТД являются газовые и инерционные силы, а в ТВД ещё и воздушный винт и редуктор.
4.1. СВОБОДНЫЕ КРУТИЛЬНЫЕ КОЛЕБАНИЯ ДВУХМАССОВОЙ СИСТЕМЫ
Рассмотрим расчётную схему системы состоящей из двух дисков с моментами инерции
Рис.4.2. Расчетная схема ротора с двумя дисками
Приложим к системе крутящий момент Отклонение сосредоточенных масс относительно положения равновесия происходит в разные стороны, поэтому на валу имеется сечение, которое остаётся неподвижным. Это сечение (точка О на рис.4.2.) называется узлом колебаний. При различных Так как узел колебаний остается неподвижным, то можем считать его заделкой вала и перейти от двухмассовой системы к двум одномассовым системам с одинаковой частотой колебаний (рис.4.2), которую можно рассчитать по зависимости
Жёсткости участков вала равны
где Подставим (4.2) в тождество (4.1), получим
так как
Частота крутильных колебаний равна
Подставим в (4.5) выражение для
где Уравнения колебаний двух одномассовых систем (рис. 4.2), при отсутствии сил сопротивления, определяется значениями углов закрутки
Амплитуды колебаний
Амплитуды
Знак минус означает, что массы колеблются в разные стороны. 4.2. СВОБОДНЫЕ КРУТИЛЬНЫЕ КОЛЕБАНИЯ МНОГОМАССОВЫХ СИСТЕМ
Рассмотрим крутильную систему, состоящую из четырех сосредоточенных масс с моментами инерции
Рис. 4.3. Расчетная схема многодисковых роторов
Составим дифференциальное уравнение колебаний, используя уравнение Лагранжа второго рода
где
где
Определим частные производные от кинетической энергии по угловой скорости
Производные по времени от частных производных (4.12)
Частные производные от потенциальной энергии по углу закрутки
Подставим уравнения (4.13) и (4.14) в уравнение (4.10), получим систему четырёх линейных дифференциальных уравнений второго порядка
Углы поворота i- ой массы по аналогии с уравнением (4.7) определяются
Дифференцируя дважды уравнения (4.16), получим:
Подставим уравнения (4.16) и (4.17) в систему (4.15), получим уравнения для определения амплитуд и частоты колебаний
В системе четырёх уравнений содержится пять неизвестных: частота Преобразуем систему уравнений (4.18), сгруппировав одноименные амплитуды
Амплитуды в системе уравнений (4.19) будут отличны от нуля, если определитель системы равен нулю. Запишем определитель в виде степенного ряда
Решение уравнения (4.20) относительно квадрата частоты Система, имеющая Четырёхмассовая система имеет три критических формы колебаний: (когда частота вынужденных колебаний совпадает с частотой собственных колебаний) одноузловую, двухузловую, трёхузловую и соответственно три критических частоты колебаний (рис.4.3). 4.3. ПРИВЕДЕНИЕ РЕАЛЬНОЙ КРУТИЛЬНОЙ СИСТЕМЫ К ЭКВИВАЛЕНТНОЙ РАСЧЕТНОЙ
Формулы приведения рассмотрим на примере ТВД. Реальная крутильная система ТВД включает в себя воздушный винт, роторы компрессора и турбины, подвижные детали редуктора является сложной системой с рассредоточенными массами, соединёнными упругими валами переменного сечения. Такие системы имеют бесконечное число собственных частот и форм колебаний. Так как опасными обычно, являются две три частоты, то реальную систему заменяют теоретической, зквивалентной реальной, но существенно проще. Эквивалентная система представляет собой прямолинейный невесомый вал постоянного сечения с размещенными на нем сосредоточенными массами (рис. 4.4).
Рис. 4.4. Приведенная крутильная система одновального ТВД
При приведении реальной системы к эквивалентной необходимо, чтобы потенциальные и кинетические энергии их элементов были равны. То есть если углы закрутки реальной и приведенной системы равны то и сравниваемые массовые моменты инерции и жесткости участков вала между массами также равны. Следовательно, моменты инерции масс компрессора, турбины, винта, редуктора и других элементов ротора двигателя равны моментам инерции сосредоточенных масс расчетной системы. Приведённая длина участка вала
где Жёсткость вала, состоящего из двух участков разного диаметра, определится
где Обратная величина жесткости - податливость из (4.22) определится
То есть податливость приведённого вала равна сумме податливостей участков реального вала. При повороте вала двигателя на угол Из условия равенства кинетических энергий получим
где Аналогично определяется момент инерции редуктора
где Жёсткость участка вала между приведенными массами определяется из равенства потенциальных энергий реальной, и эквивалентных систем
Приведённая длина вала с сечением расчётной, приведенной схемы, моментом инерции
Зависимости (4.24) …(4.25) позволяют перейти от сложных реальных крутильных систем к простым расчетным схемам с эквивалентными моментами инерции, жесткостями и длинами участков валов.
4.4. ВЫНУЖДАЮЩИЕ МОМЕНТЫ И РЕЗОНАНС
В ГТД момент, приложенный к элементам ротора и вызывающий крутильные колебания, изменяется по сложному закону (рис.4.5, а).
а б Рис.4.5. Моментная (а) и частотная (б) диаграммы ротора ГТД
Для проведения анализа и выделения наиболее опасных частот и амплитуд, разложим эту зависимость в ряд Фурье:
где Когда частота вынуждающего момента, совпадает с частотой собственных крутильных колебаний ротора, наступает резонанс. Для проведения анализа и определения резонансных режимов в диапазоне изменения оборотов двигателя строится частотная диаграмма. На частотной диаграмме наносятся частоты свободных крутильных колебаний системы Частота вынуждающей силы изменяется с оборотами и определяется количеством возбуждающих факторов (количество лопастей винта, степень редукции, число лопаток направляющих и сопловых аппаратов, числом рабочих лопаток и т.д.). Резонансные режимы определяются в точках пересечения частот свободных колебаний и частот вынуждающих колебаний.
4.5. Контрольные вопросы 1. Какие элементы двигателя вызывают крутильные колебания? 2. В чем опасность крутильных колебаний роторов? 3. Что такое собственные частоты и формы крутильных колебаний? 4. Основные допущения при расчете частот и форм крутильных колебаний многомассовых роторов. 5. Как зависят собственные частоты и амплитуды колебательной системы от параметров механической системы: массы дисков, диаметров и длины валов, числа дисков и т. д.? 6.Как определить являются ли крутильные колебания в двигателе резонансными? 7.Какими мероприятиями можно сместить резонансные частоты крутильных колебаний от рабочих оборотов двигателя? 8. Как перейти от сложных реальных крутильных систем к простым? 9. Сколько форм и частот колебаний имеет ротор с двенадцатью дисками? 10. Как изменится жесткость вала при увеличении диаметра в два раза? 11. Как изменится момент инерции диска при уменьшении толщины в три раза, а диаметра в два раза?
5.ВИБРАЦИОННЫЕ ПЕРЕГРУЗКИ ДВИГАТЕЛЕЙ Работа двигателя на всех режимах неизменно сопровождается вибрацией, которая через узлы крепления передается на элементы стенда или самолета. Причинами вибрации могут быть: 1- Отклонение центра тяжести вращающихся деталей от оси ротора (дисбаланс), несбалансированность воздушного винта и вращающихся деталей редуктора; 2 – Частотный характер изменения параметров газового потока по времени, поперечному сечению и длине двигателя. Подробный анализ причин и расчет частот колебаний отдельных частей двигателя рассмотрен в разделах 2…4,6. Возникающие при работе двигателя высокочастотные колебания нагружают дополнительными переменными нагрузками детали двигателя, элементы конструкции самолета, сказываются на работе приборов и агрегатов, а также отражаются на здоровье и самочувствии пассажиров и экипажа. Допустимые значения частот и амплитуд вибрационных перегрузок могут служить критерием исправности двигателей. Поэтому при производстве двигателей, послеремонтная проверка и контроль вибрационных параметров в процессе эксплуатации двигателей является обязательным. Для оценки значения виброперегрузки применяется коэффициент виброперегрузки k, который определяется как отношение ускорения некоторой точки двигателя при колебаниях к ускорению силы тяжести. Рассмотрим схему подвески двигателя массой
Рис.5.1. Схема подвески двигателя Уравнение движения массы под действием данной силы запишется
Траектория перемещения центра тяжести массы двигателя у и её ускорение
Подставим значение ускорения центра тяжести двигателя
где Тогда коэффициент виброперегрузки определится:
Коэффициент вибрационной перегрузки может быть определён как отношение максимальной динамической силы, возникающей при колебаниях двигателя, к его весу. То есть он показывает во сколько раз силы инерции двигателя при вибрации больше силы веса. Коэффициент вибрационной перегрузки рис.5.2 изменяется с изменением оборотов ротора двигателя и резко увеличивается при вращении ротора вблизи критических угловых скоростей.
Рис.5.2. Изменение коэффициента виброперегрузки от угловой скорости Запишем формулу (5.4) через линейные частоты колебаний
где
С учетом порядка гармоники возмущающей силы
Размах колебаний S изменяется в широких пределах и зависит от порядка гармоники возмущающей силы (см. рис 2.2, рис.4.5). Для оценки вибрационного состояния двигателя вне зависимости от условий его закрепления определяется размах колебаний центра тяжести, а не произвольной точки двигателя. При этом подвеска двигателя должна обеспечивать полную свободу его перемещений. Примем, что ротор жесткий, вибрация двигателя обусловлена только несбалансированностью ротора. Движение центра тяжести двигателя в направлении оси
где Максимальное смещение центра тяжести равно
где Подставим выражение (5.8) в (5.4), получим
Таким образом, виброперегрузка двигателя, при данных допущениях, определяется только его весом, величиной дисбаланса и скоростью вращения ротора. Если бы корпус двигателя был абсолютно жестким и на него передавалась бы только неуравновешенная сила, приложенная в центре тяжести, то траектории всех точек двигателя, а, следовательно, и коэффициенты перегрузок, замеренные в любой его точке имели бы одно и то же значение. В реальном двигателе на корпус действуют момент и сила не проходящие через центр тяжести двигателя, и каждая точка двигателя участвует в поступательном движении вместе с центром тяжести и во вращательно движении вокруг него. При этом траектории точек двигателя зависят от расстояния до центра тяжести двигателя. Также сам корпус двигателя не является абсолютно жестким, поэтому амплитуды колебаний различных его точек также неодинаковы и зависят от амплитуды колебаний корпуса и ли его частей. При доводке двигателя выбираются точки, колебания которых наиболее точно характеризуют его вибрационное состояние. Эти точки лежат в плоскости основных узлов крепления двигателя к самолету или в плоскости опор двигателя. Хотя коэффициент виброперегрузки, определяемый на стенде, не соответствует коэффициенту виброперегрузки самого двигателя, тем не менее, он дает возможность проводить сравнение двигателей между собой и с эталоном. Величина виброперегрузки является критерием совершенства и технического состояния двигателя. Виброперегрузка двигателя определяется не только величиной дисбаланса, но и появлением критических оборотов ротора в рабочем диапазоне скоростей вращения, возникновением деформаций составного ротора при недостаточной жесткости его элементов, а также внешними эксплуатационными условиями. Допустимое значение виброперегрузок определяется и типом самолета, чем больше масса самолета, тем большее значение коэффициента виброперегрузок можно допустить. Для снижения влияния виброперегрузок на самолет применяются различные способы подвески двигателей на амортизаторах.
5.1. БАЛАНСИРОВКА РОТОРОВ ГТД
В реальных роторах ГТД при их вращении всегда действуют инерционные силы и моменты от неуравновешенных масс, из-за неточности изготовления и сборки, неоднородностей: материала, упругих и остаточных деформаций деталей ротора. Эти нагрузки передаются на опоры роторов, нагружая дополнительно их подшипники, и вызывают вибрацию двигателя. Через узлы крепления двигателя к самолету переменные по величине и направлению нагрузки передаются на самолет, вызывая вибрации и дополнительные нагрузки в элементах конструкции и оборудования, ослабляют места стыков конструкции планера и трубопроводов, дополнительный шум, а также влияют на самочувствие и здоровье пассажиров и экипажа. В процессе работы двигателя могут возникать резонансные режимы, вызывающие дополнительные вибрационные напряжения в отдельных деталях двигателя, самолета или оборудования, что может привести к их поломке. Для предотвращения колебаний с недопустимыми амплитудами, снижения влияния виброперегрузок на надежность и ресурс двигателя, самолета и оборудования проводится как статическая, так и динамическая балансировка роторов двигателей, как при производстве, так и при ремонтах. Статическая балансировка Если положить вал с тонким диском, у которого центр тяжести смещен относительно оси вала на величину е, на острые строго отгоризонтированные параллельные брусья, то момент от силы веса, относительно оси вращения, заставит диск поворачиваться относительно оси, до положения устойчивого равновесия, при котором центр тяжести располагается в наинизшей точке (рис.5.3). Такой ротор (диск) называется статически неуравновешенным.
Рис.5.3 Схема статической балансировки
Для устранения дисбаланса необходимо создать равный и противоположно направленный момент путем размещения на диаметральной стороне диска груза весом Gy на расстоянии r от оси вращения. Условие равновесия, при котором диск будет находиться в безразличном равновесии в окружном направлении, запишется
Статическую балансировку проходят все вращающиеся детали двигателя. Обычно статическая балансировка осуществляется путем снятия металла со специально предусмотренных при конструировании поверхностей деталей. Допустимое значение дисбаланса указывается в конструкторской документации.
Динамическая балансировка
Рассмотрим ротор установленный в опорах и нагруженный неуравновешенной силой Р имоментом М (рис.5.4). При вращении ротора неуравновешенная сила Р имомент М изменяются пропорционально квадрату угловой скорости Уравновешивание осуществляется двумя грузами, расположенными в двух произвольно выбранных плоскостях, называемых плоскостями приведения.
Рис. 5.4, Схема динамической неуравновешенности роторов
Возьмем за плоскости приведения плоскости, проходящие через подшипники и перпендикулярные оси вала. Неуравновешенную силу Р можно заменить двумя составляющими силами
а момент М - парой сил Q, действующих в плоскостях приведения:
Равнодействующие сил
Таким образом, неуравновешенная сила Для статической и динамической балансировки ротора необходимо в плоскостях приведения диаметрально противоположно силам
где Для ротора работающего без прогиба вала Динамическая балансировка неокончательно обработанных роторных деталей (отсутствие полировки, упрочняющих и антикоррозионных покрытий и т.д.) обычно проводится за счет снятия металла в специально предусмотренных конструктором местах, желательно на максимальном радиусе. Окончательная балансировка ротора проводится подбором по массе и соответствующим размещением рабочих лопаток, ввертыванием балансировочных винтов, высверливанием фиксирующих штифтов, ввертыванием балансировочных грузов и другие способы, обеспечивающие динамическую балансировку и не нарушающие прочностные качества ротора и газодинамические параметры двигателя. Для повышения ресурса двигателя, снижения уровня вибраций необходимо снижать значение остаточного дисбаланса. Однозначно, чем меньше размеры двигателя и чем меньше скорость вращения ротора, тем большее значение допустимого дисбаланса для двигателя. Нагрузка на подшипник от неуравновешенных масс подсчитывается по формуле
Динамическая балансировка ротора с учетом прогиба ротора отличается от рассмотренной выше методики, так как масса балансировочных грузов зависит от скорости вращения ротора. Поэтому гибкие ротора, обычно балансируются, для одной угловой скорости вращения ротора. Для гибкого ротора неуравновешенная центробежная сила определяется по формуле
Влияние неуравновешенности ротора с учетом прогиба вала при изменении угловой скорости вращения снижают путем снижения интенсивности прогиба. С этой целью осуществляют демпфирование колебаний при критических режимах, установкой балансировочных грузов в плоскости действия неуравновешенных центробежных сил и т.д.
5.2. Контрольные вопросы
1. Назовите причины вибрации ГТД при работе? 2. Дайте определение коэффициенту вибрационной перегрузки. 3. Какими параметрами определяется виброперегрузка двигателя? 4. Методы определения и снижения виброперегруки двигателя. 5. Что такое статическая балансировка роторов? 6. Что такое динамическая балансировка роторов? 7. Дайте определение дисбаланса.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.53 (0.011 с.) |

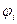 (рис.4.1), вызывая на валу и других упругих элементах ротора напряжения кручения, которые могут быть причиной усталостного излома.
(рис.4.1), вызывая на валу и других упругих элементах ротора напряжения кручения, которые могут быть причиной усталостного излома.
 , соединенных упругим валом, установленным в двух опорах (рис.4.2). Вал одного диаметра а, следовательно, и с постоянной крутильной жёсткостью
, соединенных упругим валом, установленным в двух опорах (рис.4.2). Вал одного диаметра а, следовательно, и с постоянной крутильной жёсткостью  .
.
 и, закрутим вал на угол
и, закрутим вал на угол  . После мгновенного снятия нагрузки система будет совершать крутильные колебания за счет сил инерции и упругости вала.
. После мгновенного снятия нагрузки система будет совершать крутильные колебания за счет сил инерции и упругости вала. (4.1)
(4.1) ;
;  (4.2)
(4.2) - полярный момент инерции сечения вала, постоянный по длине; G - модуль сдвига.
- полярный момент инерции сечения вала, постоянный по длине; G - модуль сдвига. (4.3)
(4.3) , то
, то
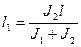 (4.4)
(4.4) (4.5)
(4.5)
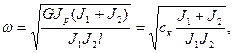 (4.6)
(4.6) - жесткость всего вала.
- жесткость всего вала. :
: (4.7)
(4.7) равны углам закрутки масс дисков под действием статического крутящего момента
равны углам закрутки масс дисков под действием статического крутящего момента 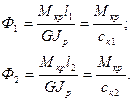 (4.8)
(4.8) (4.9)
(4.9) соединенных между собой упругими валами с жесткостью
соединенных между собой упругими валами с жесткостью  (рис.4.3).
(рис.4.3).
 (4.10)
(4.10) - суммарные кинетическая и потенциальная энергия масс системы
- суммарные кинетическая и потенциальная энергия масс системы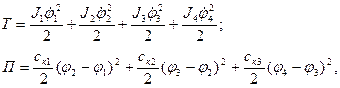 (4.11)
(4.11) - ой массы;
- ой массы; угловая скорость.
угловая скорость.


 . (4.12)
. (4.12)


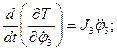
 (4.13)
(4.13)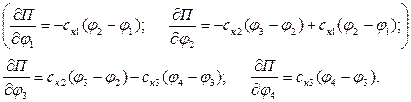 (4.14)
(4.14) (4.15)
(4.15)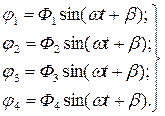 (4.16)
(4.16) (4.17)
(4.17) (4.18)
(4.18)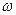 и амплитуды
и амплитуды 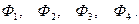
 (4.19)
(4.19) (4.20)
(4.20) даёт четыре корня, один корень равен нулю и три
даёт четыре корня, один корень равен нулю и три  отличные от нуля. Таким образом, мы получили, что четырёхмассовая система имеет три частоты и три формы собственных колебаний.
отличные от нуля. Таким образом, мы получили, что четырёхмассовая система имеет три частоты и три формы собственных колебаний.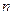 сосредоточенных масс, будет иметь
сосредоточенных масс, будет иметь 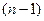 собственных частот и форм колебаний.
собственных частот и форм колебаний.
 находится из равенства жесткостей вала расчетной и реальной схемы
находится из равенства жесткостей вала расчетной и реальной схемы (4.21)
(4.21) - момент инерции сечения расчетной системы;
- момент инерции сечения расчетной системы;  - длина реального вала.
- длина реального вала. (4.22)
(4.22) - крутящий момент;
- крутящий момент;  - углы закрутки вала на первом и втором участке вала с постоянным диаметром.
- углы закрутки вала на первом и втором участке вала с постоянным диаметром. (4.23)
(4.23) вал винта повернется на угол
вал винта повернется на угол  , где
, где 
 , (4.24)
, (4.24) - момент инерции винта.
- момент инерции винта.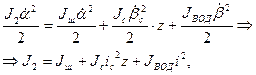 (4.25)
(4.25) - моменты инерции: ведущей шестерни редуктора относительно оси её вращения, сателлита относительно его оси вращения, водила;
- моменты инерции: ведущей шестерни редуктора относительно оси её вращения, сателлита относительно его оси вращения, водила; 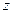 - число сателлитов;
- число сателлитов;  - угол поворота сателлита при повороте ведущей шестерни на угол
- угол поворота сателлита при повороте ведущей шестерни на угол  - передаточное отношение от ведущей шестерни к сателлиту);
- передаточное отношение от ведущей шестерни к сателлиту);  , (4.26)
, (4.26) - жёсткость участка вала от винта до центральной ведущей шестерни.
- жёсткость участка вала от винта до центральной ведущей шестерни. , определится
, определится . (4.27)
. (4.27)
 (4.28)
(4.28) - средний постоянный момент;
- средний постоянный момент;  - амплитуда
- амплитуда 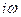 - частота
- частота  - фазовый угол.
- фазовый угол. (горизонтальные линии на рис.4.5, б.) и прямые выходящие из начала координат отображающие изменение частот вынужденных колебаний
(горизонтальные линии на рис.4.5, б.) и прямые выходящие из начала координат отображающие изменение частот вынужденных колебаний  .
.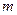 (рис.5.1), на который в направлении оси у действует возмущающая сила Р0, изменяющаяся по гармоническому закону.
(рис.5.1), на который в направлении оси у действует возмущающая сила Р0, изменяющаяся по гармоническому закону.
 (5.1)
(5.1) под действием силы Р0 определится
под действием силы Р0 определится (5.2)
(5.2) , (5.3)
, (5.3) - максимальное ускорение массы двигателя.
- максимальное ускорение массы двигателя.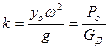 (5.4)
(5.4)
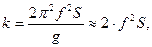 (5.5)
(5.5) - линейная частота колебаний;
- линейная частота колебаний; - размах колебаний, м.
- размах колебаний, м. . (5.6)
. (5.6) запишется
запишется (5.7)
(5.7) - масса ротора;
- масса ротора;  - максимальное значение дисбаланса ротора.
- максимальное значение дисбаланса ротора. , (5.8)
, (5.8) - статический дисбаланс ротора.
- статический дисбаланс ротора. (5.9)
(5.9)
 (5.10)
(5.10) . Такая неуравновешенность называется динамической и для уравновешивания таких роторов проводится динамическая балансировка.
. Такая неуравновешенность называется динамической и для уравновешивания таких роторов проводится динамическая балансировка.
 и
и  , (5.11)
, (5.11)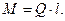 (5.12)
(5.12) и
и  в плоскостях приведения равны суммам векторов соответствующих сил
в плоскостях приведения равны суммам векторов соответствующих сил (5.13)
(5.13) и
и  , действующими в плоскостях приведения и изменяющимися пропорционально квадрату угловой скорости вращения ротора
, действующими в плоскостях приведения и изменяющимися пропорционально квадрату угловой скорости вращения ротора  (5.14)
(5.14) и
и  - радиусы крепления балансировочных грузов;
- радиусы крепления балансировочных грузов; 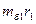 и
и  - динамический дисбаланс в данной плоскости. Также возможна динамическая балансировка путем снятия металла в плоскостях приведения в направлении действия сил R.
- динамический дисбаланс в данной плоскости. Также возможна динамическая балансировка путем снятия металла в плоскостях приведения в направлении действия сил R. (ротор жесткий) потребная масса балансировочного груза не зависит от угловой скорости вращения, так как уравновешиваемая сила R и центробежная сила от балансировочных грузов находятся в одинаковой, функциональной зависимости от неё.
(ротор жесткий) потребная масса балансировочного груза не зависит от угловой скорости вращения, так как уравновешиваемая сила R и центробежная сила от балансировочных грузов находятся в одинаковой, функциональной зависимости от неё. (5.15)
(5.15) (5.16)
(5.16)


