
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет критической скорости вращения ротора с учётом гироскопического моментаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
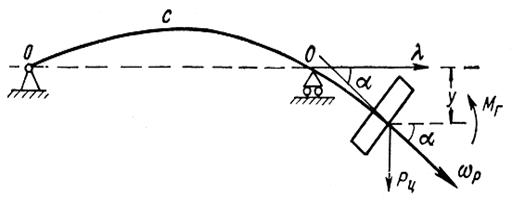
Рассмотрим расчётную схему ротора, когда на прогиб вала помимо центробежной силы действует ещё и гироскопический момент (рис. 3.12).
Рис. 3.12. Расчетная схема ротора Из принципа независимости действия сил на упругие системы, для прогиба вала у, от действия центробежных сил
где Центробежная сила инерции диска и гироскопический момент определяются по ранее выведенным формулам
Подставим уравнения (3.60) и (3.61) в зависимости (3.59), получим
Решением уравнения (3.62) являются прогиб
При равенстве знаменателя выражений (3.63) нулю прогиб
Единичные перемещения и
где Для роторов с валами постоянного сечения и одним диском, двух классических схем установки в опорах и размещения дисков, коэффициенты влияния можно определить по формулам, приведенным в таблице 3.1. Коэффициенты влияния от моментов и сил Таблица 3.1
3.5. РАСЧЕТ КРИЧЕСКИХ СКОРОСТЕЙ ВРАЩЕНИЯ МНОГОДИСКОВЫХ РОТОРОВ Рассмотрим вал с k дисками произвольно расположенными по валу (рис. 3.13). Масса вала может быть учтена за счет разбивки вала на участки и отнесения масс участков к массам соответствующих дисков. Обозначим прогибы вала от масс дисков и участков вала в местах расположения дисков как
Рис.3.13. Ротор с несколькими дисками
Вал вращается с угловой скоростью Обозначим работу центробежных сил на этих участках через При всех скоростях вращения, кроме Таким образом, величина критической скорости вращения многодискового ротора, должна определяться из условия
Потенциальная энергия изогнутого вала определяется
Работа центробежных сил и гироскопических моментов при скорости вращения
Приравнивая работу центробежных сил и гироскопических моментов (3.68) потенциальной энергии деформации получим
откуда выразим
По формуле (3.70) может быть определена критическая угловая скорость, если задаться изогнутой осью вала. Для определения первой критической скорости в качестве изогнутой оси ротора принимается изогнутая ось от массы дисков и участков вала. При этом зависимость для расчета
В подкоренном выражении числитель это удвоенная потенциальная энергия деформации при изгибе вала весом дисков и может быть определен по зависимости
Подставим выражения (3.72 в формулу (3.71)
Если пренебречь влиянием гироскопического момента то зависимость (3.73) примет вид
Пренебрегая влиянием на критические скорости вращения роторов
Примем, что изогнутая ось вала с несколькими дисками подобна изогнутым осям с каждым из дисков в отдельности, тогда каждое из слагаемых в выражении (3.75) представляет величину обратную квадрату критической угловой скорости вала с одним диском. Тогда из выражения (3.75) получаем приближенную формулу расчета критических скоростей вращения роторов с несколькими дисками (формула Данкерли)
Таким образом, критическую скорость вращения многодисковых роторов можно определить через критические скорости простейших систем, (рис.3.14).
Рис.3.14. Расчетная схема многодискового ротора: 1-весомый вал без дисков; 2,3,4 – невесомый вал с одним диском
По данному методу ротор, состоящий из вала, установленного в опорах и нескольких дисков, размещённых произвольным образом по длине вала, разбивается на простейшие системы - весомый вал без дисков; - невесомый вал с дисками, размещёнными на определённом расстоянии от опор. Критическая скорость ротора рассчитывается по зависимости:
где Критические скорости вращения весомого вала рассчитываются в зависимости от способа установки в опорах по формулам (3.41)…(3.43). Для расчёта критической скорости невесомого вала с одним
3.6. ПРИВЕДЕНИЕ СЛОЖНЫХ ИЗГИБНЫХ СИСТЕМ К ЭКВИВАЛЕНТНЫМ
Ротор реального ГТД многоопорный и, обычно состоит из роторов компрессора и турбины, соединенных посредством муфты. Ротора, как компрессоров, так и турбин представляют из себя сложную, упругую систему с рассредоточенными массами дисков сложной формы и переменной по длине жёсткостью вала. Для облегчения расчёта критических скоростей вращения сложных роторов их заменяют на более простые, динамически эквивалентные системы, состоящие из упругого невесомого вала и закреплённых на них дисков. Число масс и их расположение на валу выбираются в соответствии с расположением масс в реальном роторе, а рассредоточенные массы вала, барабанов и других элементов приводят к одной или нескольким массам эквивалентной системы или добавляют к массам дисков. Приведенные массы, моменты инерции этих масс и жесткости участков эквивалентной системы выбираются из условия обеспечения идентичности частот и форм колебаний эквивалентной системы реальному ротору. Приведённую массу эквивалентной системы определяют из условия равенства кинетических энергий колебания реальной и эквивалентных систем. Не останавливаясь подробно на выводе, запишем выражения для расчёта эквивалентных масс наиболее распространенных простых схем. Двухопорный вал с диском посередине (рис. 3.9,а). Приведённая масса определяется по выражению
где Двухопорных вал с диском расположенным на произвольном расстоянии х от опоры (рис.3.9,б). За место приведения принимается место расположения диска. Приведённая масса определяется по формуле
Двухопорный вал с диском расположенным консольно (рис.3.9, в). За точку приведения масс также принимают место расположения диска. Приведённая сосредоточенная масса рассчитывается:
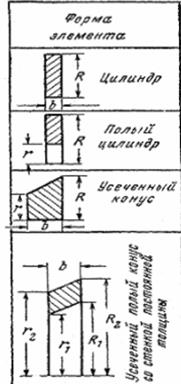
где х – текущая координата по длине вала; Массу вала многодискового ротора присоединяют к массе одного из дисков, или если масса вала существенно меньше массы ротора её пренебрегают. Определение приведенных моментов инерции. Диски компрессоров, турбин с фланцами, буртами и другими конструктивными элементами имеют сложную форму. Массовый момент инерции сложных пространственных фигур определяют как сумму моментов инерции простейших тел вращения, на которые разбивается диск. Зависимости по определению моментов инерции и масс простейших тел вращения приведены в таблице 3.2.
Моменты инерции простейших тел Таблица 3.2
Суммарный полярный момент инерции диска сложной пространственной формы, состоящий из
Экваториальный момент инерции элемента диска относительно его диаметра, проходящего через центр тяжести элемента равен
Экваториальный момент инерции всего диска относительно диаметра, проходящего через центр тяжести диска, определяется по зависимости
где При размещении на диске рабочих лопаток также определяется приведенный момент инерции. Полярный момент инерции комплекта из z лопаток, массой -
Экваториальный момент инерции комплекта лопаток относительно диаметра, проходящего через центр тяжести диска, равен
где Для всего ротора имеем
где Итак, роторы ГТД при вращении, под действием неуравновешенных масс при определенных частотах могут терять устойчивость. При этом амплитуды колебаний резко возрастают, поэтому работа роторов на данных режимах недопустима. Приведенные зависимости позволяют проводить расчеты по определению критических скоростей вращения реальных роторов и назначить безопасные стационарные режимы работы двигателей.
3.7. Контрольные вопросы 1. Приведите факторы, вызывающие колебания роторов. 2. Какая скорость вращения ротора называется критической? 3. Дайте определение жесткости системы. 4. Чем отличается динамическая жесткость от статической. 5. Зачем при расчете критических скоростей необходимо рассматривать сложные системы «ротор - корпус»? 6.Назовите факторы, влияющие на критические скорости вращения роторов. 7. Почему работа роторов на критических скоростях вращения недопустима? 8. Способы борьбы с опасными колебаниями роторов двигателей. 9. Как рассчитать критическую скорость многодискового ротора. 10. Объясните влияние гироскопического момента на критические скорости вращения роторов.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 981; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.008 с.) |

 и угла поворота
и угла поворота  от гироскопического момента МГ можем записать
от гироскопического момента МГ можем записать , (3.59)
, (3.59)
 - прогиб и угол поворота от единичной силы
- прогиб и угол поворота от единичной силы 
 - прогиб и угол поворота от единичного момента
- прогиб и угол поворота от единичного момента 
 (3.60)
(3.60) (3.61)
(3.61) (3.62)
(3.62) и угол поворота
и угол поворота  (3.63)
(3.63) и определяется по зависимости
и определяется по зависимости =0 (3.64)
=0 (3.64) и углы поворота
и углы поворота  , называются коэффициентами влияния и определяются через интегралы Мора
, называются коэффициентами влияния и определяются через интегралы Мора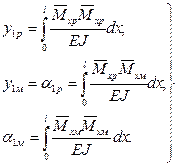 , (3.65)
, (3.65) - изгибающие моменты в сечениях вала от единичной силы
- изгибающие моменты в сечениях вала от единичной силы  =1 и единичного изгибающего момента
=1 и единичного изгибающего момента  =1.
=1.

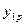








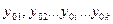 (рис.3.13).
(рис.3.13).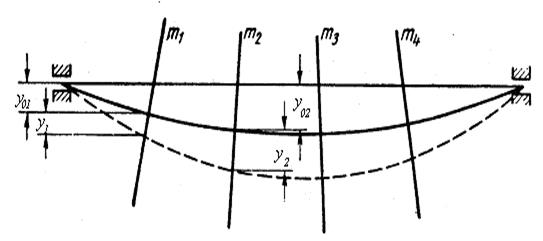
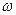 и под действием центробежной силы
и под действием центробежной силы 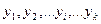 .
. , и потенциальную энергию дополнительной деформации вала как
, и потенциальную энергию дополнительной деформации вала как  .
. , вращение вала устойчиво, так как при любом возмущающем воздействии при его удалении из-за
, вращение вала устойчиво, так как при любом возмущающем воздействии при его удалении из-за  появляется дополнительная восстанавливающая сила
появляется дополнительная восстанавливающая сила 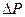 приводящая вал в первоначальное состояние.
приводящая вал в первоначальное состояние. (3.66)
(3.66) (3.67)
(3.67)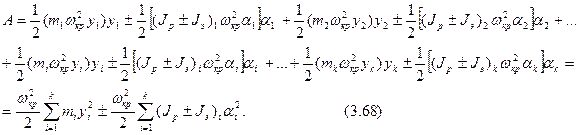
 (3.69)
(3.69) (3.70)
(3.70) (3.71)
(3.71) (3.72)
(3.72) (3.73)
(3.73)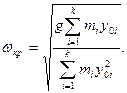 (3.74)
(3.74)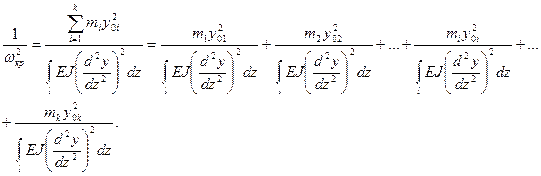 (3.75)
(3.75) (3.76)
(3.76)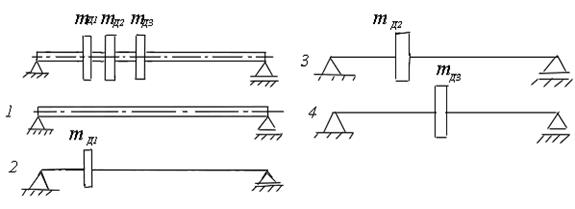
 , 3.77)
, 3.77) - критическая угловая скорость вращения весомого вала без дисков;
- критическая угловая скорость вращения весомого вала без дисков; 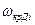 - критическая угловая скорость вращения невесомого вала с одним
- критическая угловая скорость вращения невесомого вала с одним  - тым диском.
- тым диском. (3.78)
(3.78) и
и  массы диска и вала, соответственно.
массы диска и вала, соответственно. (3.79)
(3.79) , (3.80)
, (3.80) - расстояние между опорами вала.
- расстояние между опорами вала.
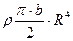






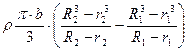
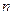 простых тел вращения определяется
простых тел вращения определяется (3.81)
(3.81)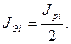 (3.82)
(3.82) (3.83)
(3.83) - масса
- масса  го элемента;
го элемента;  -расстояние от центра тяжести
-расстояние от центра тяжести  , с центром тяжести расположенным на расстоянии
, с центром тяжести расположенным на расстоянии  от оси вращения определится
от оси вращения определится (3.84)
(3.84) (3.85)
(3.85) - расстояние от центра тяжести комплекта лопаток до центра тяжести диска или приведённой массы диска вдоль оси вращения ротора.
- расстояние от центра тяжести комплекта лопаток до центра тяжести диска или приведённой массы диска вдоль оси вращения ротора. (3.86)
(3.86) - число комплектов лопаток, моменты инерции которых приводятся к данному диску или приведённой массе дисков.
- число комплектов лопаток, моменты инерции которых приводятся к данному диску или приведённой массе дисков.


