
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт лопаток компрессоров и турбин на прочностьСодержание книги
Поиск на нашем сайте При работе двигателя на лопатки компрессора и турбины действуют статические динамические и температурные нагрузки, вызывающие сложные температурные напряжения, напряжения растяжения, кручения, изгиба. Динамические нагрузки обусловлены колебанием лопаток и частотным характером приложенных нагрузок и их аналитическое определение довольно сложно, поэтому определение динамических напряжений обычно проводят экспериментально. Температурные напряжения также носят циклический характер и обусловлены неравномерным распределением температуры по лопатке при запуске и останове. Ввиду сложности расчётного алгоритма влияние температурных напряжений учитывается при задании допустимых напряжений и коэффициентов запасов прочности. Мы будем рассматривать расчет прочности лопаток от действия только статических нагрузок таких как: - центробежные силы вращающихся масс; - газодинамические нагрузки; - инерционные нагрузки при взлёте, посадке и эволюциях самолёта. Всё многообразие статических нагрузок можно разделить на растягивающие и изгибающие силы и моменты от действия, которых в материале лопаток возникают напряжения растяжения, изгиба и кручения. При расчёте напряжений в лопатках приняты следующие допущения: - лопатка рассматривается как консольная балка с жёсткой заделкой; - напряжения по каждому виду деформаций определяется независимо (что не совсем справедливо, особенно для сильно закрученных лопаток); - температура по сечению лопатки постоянна; - лопатка считается жёсткой, деформациями лопатки от нагрузок пренебрегаем; - все деформации лопатки упругие. Исходными данными для проведения прочностных расчётов лопаток являются результаты термодинамического и газодинамического расчетов компрессора или турбины.
1.1 РАСЧЕТ НАПРЯЖЕНИЙ РАСТЯЖЕНИЯ
При работе двигателя на вращающуюся с угловой скоростью
Рис.1.1 Расчетная схема лопатки
На выделенный элемент будет действовать элементарная центробежная сила dPЦ .
где Центробежная сила, действующая в сечении лопатки F от всей массы лопатки расположенной выше радиуса r, определяется интегралом
При постоянной площади сечения лопатки по радиусу
а напряжения растяжения
Как следует из выражения (1.4), значение напряжения растяжения
Лопатки с постоянной площадью по высоте из-за больших напряжений в корневом сечении не применяются в ГТД. Обычно лопатку профилируют с уменьшающейся площадью от корневого сечения к периферии. Изменение площади поперечного сечения лопатки может быть задано аналитически, либо газодинамическому расчёту в заданных сечениях. Рассмотрим расчёт напряжений растяжения в лопатке при задании изменения площади поперечного сечения по зависимости
где
где q – показатель степени, определяющий закон изменения площади лопатки по высоте (рис.1.2). q > 1- параболический закон изменения площади; q = 1 - линейный закон; q < 1 - гиперболический закон. Подставим зависимость(1.6) в выражение (1.1)
Интегрируя (1.8) получим
Напряжения растяжения в сечении z определится
Рис. 1.2. Изменение площади лопатки по высоте
Характерные законы изменения напряжений по высоте лопатки в зависимости от закона изменения площади приведены на рис.1.3.
Рис. 1.3 Распределение напряжений растяжения по высоте лопатки от ц/б сил
Из графиков видно, что изменение площади лопатки по высоте существенно влияет не только на абсолютное значение напряжения, но и на вид зависимости изменения напряжений и максимальные напряжения растяжения могут быть не только в корневом сечении лопатки, но и на некотором удалении от него. Часто закон изменения площади лопатки по высоте выразить аналитической зависимостью не возможно. В этом случае задача определения напряжений растяжения от центробежных сил решается методами конечных разностей. При этом от бесконечно малых величин dz переходят к конечно малым величинам
Рис.1.4 К расчету напряжений в лопатке методом конечных разностей Напряжения растяжения
где i- номер сечения, расположенного на расстоянии сечения; Элементарный объём участка лопатки высотой
где Расстояние от оси вращения до центра тяжести i -того элемента
где
Точность расчёта повышается с увеличением числа разбиений, обычно лопатку разбивают по высоте на шесть – десять сечений и расчеты заносят в таблицу. Так как при газодинамическом расчёте определены профили только трех сечений лопатки (корневого, среднего и периферийного), то строится график изменения площади лопатки, по которому определяются площадь любого i -того сечения рис. 1.2. По результатам расчетов строятся графики изменения напряжения лопаток по высоте (рис.1.3). Если лопатка имеет бандажную полку, то напряжения растяжения в лопатке увеличиваются на величину напряжений создаваемых бандажной полкой. Напряжения от бандажной полки в i - том сечении рассчитываются по формуле (рис.1.3)
(1.15)
где Рцб- центробежная сила от бандажа, постоянная величина для пера лопатки
где 1.2 РАСЧЁТ ИЗГИБАЮЩИХ МОМЕНТОВ
Изгибающие моменты, действующие на перо лопатки рабочего колеса компрессора или турбины ГТД, обусловлены действием центробежных и газовых сил. На лопатки направляющих аппаратов компрессоров и сопловых аппаратов турбин действует только изгибающий момент от газовых сил.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

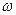 лопатку будет действовать центробежная сила. Примем следующую расчетную схему рис. 1.1. Выделим в лопатке высотой l= (RН-Rк), закреплённой на радиусе RК в ободе диска, на радиусе r от оси вращенияэлемент высотой dz.
лопатку будет действовать центробежная сила. Примем следующую расчетную схему рис. 1.1. Выделим в лопатке высотой l= (RН-Rк), закреплённой на радиусе RК в ободе диска, на радиусе r от оси вращенияэлемент высотой dz. 

 (1.1)
(1.1) - плотность материала лопатки;
- плотность материала лопатки;  (1.2)
(1.2) центробежная сила определится
центробежная сила определится (1.3)
(1.3) (1.4)
(1.4)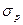 не зависит от площади поперечного сечения лопатки F, а определяется толькоугловой скоростью
не зависит от площади поперечного сечения лопатки F, а определяется толькоугловой скоростью  (1.5)
(1.5) , (1.6)
, (1.6) - коэффициент, определяемый по площадям в корневом и периферийном сечениях
- коэффициент, определяемый по площадям в корневом и периферийном сечениях , (1.7)
, (1.7) . (1.8)
. (1.8) (1.9).
(1.9). (1.10)
(1.10)

 . Лопатка по высоте разбивается на ряд участков (рис.1.4) и каждому участку, начиная с периферии, присваивается порядковый номер (
. Лопатка по высоте разбивается на ряд участков (рис.1.4) и каждому участку, начиная с периферии, присваивается порядковый номер ( ).
).
 (1.11)
(1.11) от корневого
от корневого - объём выделенного i – того участка элемента; riц – расстояние от оси вращения до центра тяжести i –того участка.
- объём выделенного i – того участка элемента; riц – расстояние от оси вращения до центра тяжести i –того участка. определяется
определяется (1.12)
(1.12) - среднее значение площади на i - том участке.
- среднее значение площади на i - том участке. (1.13)
(1.13) (1.14)
(1.14)
 (1.16)
(1.16) - масса бандажа, rб - расстояние от оси вращения до центра тяжести масс бандажа.
- масса бандажа, rб - расстояние от оси вращения до центра тяжести масс бандажа.


