
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт крепления лопатки замком типа «ёлочка»Содержание книги
Поиск на нашем сайте
Элементы замка крепления лопатки типа «ёлочка» нагружаются от центробежной силы масс лопаток и самого хвостовика рис.1.17, при этом в них возникают напряжения смятия, изгиба и среза, а в теле хвостовика лопатки и перемычке обода диска напряжения растяжения.
Рис.1.17. Геометрия и схема приложения сил в креплении лопатки хвостовиком типа «елочка»
Напряжения смятия в зубцах хвостовика лопатки
Суммарная площадь воспринимающая силу N, при переменной ширине хвостовика
где n- номер зубца хвостовика; Суммарную, нормальную к поверхности зубцов силу от центробежной силы лопатки и хвостовика определим, проектируя все силы на вертикальную ось и проводя преобразования
а напряжения смятия определятся
Если пренебречь силами трения, то
Напряжения изгиба у основания зуба. Напряжения изгиба у основания зуба возникает от силы
где
Подставим (1.80) в (1.79) получим
Напряжения среза у основания зуба. Напряжения обусловлены силой
Напряжение растяжения в хвостовике лопатки необходимо рассчитывать во всех сечениях так, как в каком сечении оно максимально заранее не известно. Для определения напряжений в i- том сечении хвостовика (рис. 1.17), составим равновесия сил на радиальное направление
где Подставим
с учётом того, что
Напряжения растяжения в перемычке обода обусловлено действием центробежных сил масс лопаток и массы самой перемычки выше расчётного сечения рис.1.18.
Рис. 1.18. Расчет схема обода диска
Составим уравнение равновесия сил действующих на перемычку обода в расчетном сечении
где Подставим
Рис. 1.19. Распределение напряжений в хвостовике лопатке и ободе диска
В хвостовике замка лопатки обычно максимальные напряжения реализуются по первой впадине от корневого сечения лопатки, а в ободе диска по последней впадине от наружного диаметра (рис.1.19). Рабочие лопатки, лопатки сопловых и направляющих аппаратов ГТД в процессе работы нагружены центробежными, инерционными силами, что вызывает в пере лопаток, узлах их крепления в ободе диска значительные напряжения, которые не должны превышать допустимые для данного материала. Полученные зависимости, позволяют на этапе проектировать назначать конструктивные размеры лопаток, обеспечивающие требуемые запасы прочности, а также анализировать прочностные параметры лопаток эксплуатируемых двигателей.
1.5. Контрольные вопросы
1. Назовите силы, действующие на рабочие, сопловые и направляющие лопатки ГТД на крейсерском режиме полета; 2. Приведите расчетную схему и основные уравнения изгибающих моментов действующих на лопатку от газового потока; 3. Приведите расчетную схему и основные зависимости расчета изгибающих моментов от центробежных сил. 4. Составьте расчетную схему определения напряжений изгиба в пере лопатки от газовых и центробежных сил; 5. Обоснуйте целесообразность выноса центра тяжести лопаток от радиального направления; 6. Назовите основные силы, учитывающиеся при расчете крепления лопаток замком типа ласточкин хвост; 7. Составьте расчетную схему по определению напряжений смятия, изгиба в креплении лопатки замком типа «ласточкин хвост»; 8. Приведите расчетную схему и основные зависимости по расчету напряжений смятия, растяжения, среза, изгиба в креплении лопаток замком типа «ёлочка»; 9. Приведите расчетную схему и основные уравнения по определению напряжений смятия в перемычке обода при креплении лопатки замком типа «ёлочка»; 10. Приведите расчетную схему и основные зависимости по определению напряжений растяжения в перемычке обода при креплении лопатки замком типа «ёлочка».
КОЛЕБАНИЕ ЛОПАТОК
Работа рабочих, направляющих и сопловых лопаток компрессоров и турбин в ГТД неизбежно сопровождается их вибрацией, что может быть причиной их разрушения. Обеспечение надежной работы лопаток ГТД является одним из важнейших вопросов в двигателестроении. Если к лопатке с жесткой заделкой в корневом сечении приложить единичный импульс силы, обеспечивающий её упругую деформацию, то лопатка начнет колебаться. Колебания лопатки без воздействия внешней силы, называются свободными или собственными. Из-за трения о воздух, гистерезиса в материале лопатке и т.д. амплитуда колебаний со временем уменьшается, т.е. свободные колебания затухающие. Если колебания лопатки происходят под воздействием внешней переменной силы, то такие колебания называются вынужденными. При совпадении частоты собственных и вынужденных колебаний наступает резонанс, при котором амплитуда резко возрастает и может произойти поломка детали. Работа изделий на резонансных режимах, особенно продолжительное время недопустима. Поэтому при разработке нового двигателя решается две динамические задачи: - определение спектра собственных частот и форм колебаний лопаток компрессоров и турбин; - определение источника и частот колебаний внешних возбуждающих сил. Источниками колебаний в ГТД могут быть: - колебания газового потока по тракту двигателя; - силы инерции вращающихся масс; - вибрация элементов двигателя и самолёта. Колебания газового потока всегда сопровождает работу ГТД. Частота и амплитуда внешних колебаний определяются: конечным числом лопаток ступеней компрессора и турбины, пульсационным горением топлива в камере сгорания, наличием в проточной части стоек, а также отклонением размеров проточной части от расчётных из-за неточности изготовления, сборки, деформаций или обгорания в процессе работы, затенения входа от обледенения и др. Так, за решеткой профилей с конечным числом лопаток, газовый поток имеет окружную неравномерность скоростей и давлений (рис.2.1), которая определяется толщиной выходной кромки лопатки и расстоянием между решётками.
Рис. 2.1 Примерная эпюра изменения давления за направляющим аппаратом
В ТВД неравномерность газового потока по тракту двигателя может быть вызвана воздушным винтом и редуктором. Так лопатка ротора вращающегося со скоростью Частота вынуждающей силы приложенной к лопатке определится:
В реальных двигателях вынуждающая сила действует не мгновенными импульсами, а растянута во времени (рис.2.2). Для удобства анализа и расчёта обычно зависимость вынуждающей силы раскладывают в ряд Фурье в виде суммы гармоник:
где
Рис.2.2. Разложение вынуждающей силы на гармоники
Частота возмущающей силы от
На величину напряжений, возникающих при колебаниях лопаток, влияет амплитуда возмущающей силы, частота и форма колебаний, прочностные характеристики материала лопаток, силы демпфирования и геометрические размеры лопаток. Точный расчёт напряжений, ввиду сложности процесса из-за отсутствия данных о величине и распределении по высоте лопатки возмущающих сил и сил сопротивления колебаниям практически невозможен даже для низших гармоник возбуждающих сил. Поэтому на практике напряжения определяют тензометрированием лопаток при натурных испытаниях. На примере изгибных колебаний лопатки постоянного профиля рассмотрим оценочный расчет напряжений в корневом сечении лопатки постоянного сечения и выясним величину динамических напряжений, и какие основные факторы влияют на величину напряжений при резонансе. Примем допущения, что амплитуда возмущающей силы постоянна по высоте лопатки и составляет часть от статической нагрузки. Напряжения изгиба в корневом сечении определятся
где
Рис. 2.3. Декремент затухания колебаний
Напряжение в корневом сечении от равномерно распределённой по длине лопатки нагрузки
Подставим выражение (2.6) в уравнение (2.4)
Обычно амплитуда первой гармоники вынуждающей газовой силы составляет 0,03… 0,05 от где Пусть при расчете получено, что напряжения в лопатке от статических сил
Таким образом, получено, что динамические напряжения в корневом сечении являются очень значительными и в 14 раз превышают напряжения Формы колебаний лопаток По форме упругих деформаций свободные колебания лопаток можно разделить на: изгибные, крутильные и сложные (изгибно-крутильные). Возможны также колебания пластинчато-изгибные, при которых происходит деформации относительно средней линии профиля (рис.2.4).
Рис. 2.4 Формы колебаний лопаток: а - изгибные; б – крутильные; в – пластинчатые При колебаниях геометрическое место точек лопатки остающееся неподвижным называется узлом колебаний. Соответственно если лопатка имеет один узел колебаний то 1-я форма, два узла 2-я форма и т.д. Число форм колебаний (число узловых линий) определяется числом сосредоточенных масс – одна масса – одна форма, две массы – две формы и т.д. (рис 2.5).
Рис. 2.5 Формы колебаний невесомого упругого стержня: а – одна масса; б - две массы
Рабочие лопатки представляют собой системы с бесконечным числом сосредоточенных масс, поэтому имеют бесконечное число форм и частот собственных колебаний.
2.1 СВОБОДНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ ПОСТОЯННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Рассмотрим колебания стержня с жёсткой односторонней заделкой постоянного поперечного сечения (рис. 2.6). Считаем прогибы малыми, а силы и моменты функции не только координат, но и времени. Выделим в стержне длиной Используя принцип Даламбера, запишем уравнение равновесия сил выделенного элемента на ось у
где
Рис.2.6. Расчетная схема колебания стержня постоянного поперечного сечения с односторонней жесткой заделкой
Приравнивая нулю сумму моментов всех сил относительно оси перпендикулярной плоскости ху, получим
Подставим выражение (2.9) в уравнение равновесия
Запишем дифференциальное уравнение изогнутой оси балки при малых прогибах
Подставим данное соотношение в выражение (2.9) и получим дифференциальное уравнение колебаний стержня
Для стержня постоянного сечения
где
Представим решения уравнения (2.13), с учетом граничных условий в виде суммы произведений функций времени
Подставим (2.15) в уравнение (2.13) получим
откуда, с учетом того, что t и х независимы друг от друга, то равенство (2.16) возможно только при условии
Для определения
где
Решение первого уравнения (2.19) имеет вид
и является уравнением гармонических колебаний с круговой частотой Решение второго уравнения (2.18) представим в форме
Дифференцируя три раза выражение (2.21), получим
С учетом полученных зависимостей уравнение (2.15) запишется
Следовательно, колебательное движение стержня является суммой бесконечно большого числа гармонических колебаний с различными частотами, каждой из которых соответствует своя форма упругой линии. Постоянные интегрирования Круговая частота
Для лопатки с заделкой в корневом сечении, граничные условия имеют вид
Используя соотношения (2.9) и (2.11) граничные условия (2.28) можно записать
или для функции
Выражения (2.22)… (2.25) запишутся
Так как,
Раскрывая определитель, имеем
Полученное уравнение является трансцендентным, имеющим бесчисленное количество корней. Первые четыре корня этого уравнения равны:
Подставим в формулу (2.26) значение
Аналогично вычисляются и другие формы колебаний. Из выражения (2.31) можем записать:
Принимая в уравнении (2.21)
Решая совместно уравнения (2.35) и (2.36) получим
Подставим (2.37) в уравнение (2.36) получим уравнения, характеризующее формы колебаний различных тонов
Различные формы колебаний лопатки приведены на рис.2.4.
2.2. РАСЧЕТ ПЕРВОЙ СОБСТВЕННОЙ ЧАСТОТЫ КОЛЕБАНИЙ ЛОПАТКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
Существует много методов теоретического определения собственных частот колебаний лопаток: энергетический, метод наложений, конечных разностей и т.д. Рассмотрим метод наложений как наиболее простой. Однако он позволяет рассчитать только 1-ю форму колебаний. Рассмотрим лопатку с заделкой в корневом сечении и примем следующую расчётную схему (рис.2.7):
Рис.2.7. Расчетная схема лопатки
Лопатку по длине Рассмотрим произвольный
При свободных колебаниях каждая точка лопатки совершает колебания с частотой
К
Подставим
Так как при свободных колебаниях лопатки силы инерции являются единственными внешними силами, то можно составить систему из
где Подставим (2.40) и (2.42) в уравнение (2.43) получим
Решение системы возможно в том случае если её определитель равен нулю
Частоты Представим определитель (2.45) в виде:
где
Коэффициенты уравнения (2.46) также можно представить в виде степенного ряда
где Приравняем (2.48) и (2.47), получим
Так как частота низших гармоник намного меньше высших, то ими можно пренебречь и тогда
и частота первой формы колебаний определится
Коэффициенты влияния
где
Подставим (2.53) в формулу (2.51)
где Факторы, влияющие на частоту собственных колебаний лопатки
Проведём анализ зависимости (2.54). При увеличении длины лопатки собственная частота первой формы колебаний уменьшается пропорционально квадрату отношения длин лопаток:
Изменение температуры лопатки изменяет модуль упругости материала
Материал лопатки характеризуется отношением Уменьшение осевых моментов инерции сечения лопатки
Также на частоту колебаний существенно влияют параметры профиля – толщина, клиновидность, трапециевидность, закрученность. Так, увеличение толщины профиля, в большей степени увеличивает жёсткость, чем массу, поэтому частота собственных колебаний также увеличивается. Увеличение клиновидности (уменьшение отношения Уменьшение трапециевидности (отношение длины хорды лопатки на периферии к длине хорды в корневом сечении Закрутка лопатки большого влияния на частоту колебаний не оказывает. На частоту собственных колебаний лопатки оказывает влияние форма перехода от пера к хвостовику, тип и форма хвостовика, а также усилие затяжки хвостовика в диске.
2.3. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ КОЛЕБАНИЯ ЛОПАТКИ В ПОЛЕ ЦЕНТРОБЕЖНЫХ СИЛ
При вращении ротора на лопатку действует центробежная сила, которая повышает частоту собственных колебаний. Центробежная сила стремится выпрямить ось лопатки, отклоняющуюся при колебаниях. Центробежная сила приводит к повышению жёсткости лопатки, как натяжение струны в музыкальных инструментах. Влияние центробежной силы возрастает с увеличением закрутки лопатки, угла установки. Бандажная полка также повышает влияние центробежной силы на увеличение собственной частоты колебаний. Кроме того, в конструкциях, где хвостовик лопатки устанавливается свободно в диске, центробежная сила увеличивает защемление хвостовика лопатки и тем самым повышает частоту собственных колебаний. Определение частоты колебаний лопатки в поле центробежных сил проведем энергетическим методом. Рассмотрим колебание лопаток с жесткой заделкой в ободе диска в плоскости наименьшей жесткости. Лопатку представим как упругую невесомую балку с приведенной массой на конце (рис.2.8). К массе приложена центробежная сила При свободных колебаниях сумма потенциальной
Рис.2.8. К расчету частоты колебаний лопатки в поле центробежных сил
В процессе колебаний приведенная масса на упругой балке отклонится на угол
где, ввиду малости Примем, что форма упругой линии лопатки близка к форме упругой линии балки, нагруженной сосредоточенной на конце силой Р, то потенциальная энергия деформации стержня будет равна этой работе
Прогиб
где Подставим значения
Кинетическая энергия соответствующая максимальной скорости, равна
При колебаниях масса перемешается по гармоническому закону
Дифференцируя уравнения (2.62), получим
Подставим (2.63) в (2.61) получим зависимость
Подставляем полученные выражения для потенциальной и кинетической энергии в (2.56), получим
Подставим в (2.66) зависимости для прогиба (2.59) и угла наклона от силы Р
получим
Обозначим
тогда (2.67) запишется
где Линейные частоты связаны с круговыми соотношениями
Частота собственных колебаний лопатки с учётом центробежной силы
Расчёт частот собственных колебаний лопатки с учётом всех факторов сложен, поэтому рассмотрим полуэмпирические зависимости. Для расчёта первой собственной частоты колебаний лопатки коэффициент В определяется: - лопатка с постоянным по длине сечением
- лопатка с переменным по длине сечением
- лопатка закрученная, переменного сечения
где
2.4. РЕЗОНАНСНЫЕ РЕЖИМЫ И СПОСОБЫ БОРЬБЫ С ОПАСНЫМИ КОЛЕБАНИЯМИ
Резонансным называется режим, при котором частота собственных колебаний лопатки совпадает с одной из гармоник возмущающей силы, т.е.
откуда
где
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.017 с.) |



 определяются по классической зависимости - напряжение равно сила, деленная на площадь
определяются по классической зависимости - напряжение равно сила, деленная на площадь (1.74)
(1.74) определится:
определится: (1.75)
(1.75)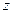 - число зубцов одной стороны замка;
- число зубцов одной стороны замка;  - высота зубцов.
- высота зубцов. (1.76)
(1.76) . (1.77)
. (1.77) . (1.78)
. (1.78) приложенной на расстоянии с от основания зуба (рис.1.17) по зависимости
приложенной на расстоянии с от основания зуба (рис.1.17) по зависимости (1.79)
(1.79) - толщина зуба у основания; с - расстояние от точки приложения силы
- толщина зуба у основания; с - расстояние от точки приложения силы  ;
;  (1.80)
(1.80) (1.81)????
(1.81)???? (1.82)
(1.82) (1.83)????
(1.83)???? - центробежная сила масс лопатки вместе с хвостовиком;
- центробежная сила масс лопатки вместе с хвостовиком;  - центробежная сила части хвостовика расположенного между двумя сечениями;
- центробежная сила части хвостовика расположенного между двумя сечениями;  - площадь расчётного сечения.
- площадь расчётного сечения. (1.84)
(1.84) , получим
, получим . (1.85)
. (1.85)
 .
. , (1.86)
, (1.86) - центробежная сила от части обода расположенного между лопатками выше расчётного сечения;
- центробежная сила от части обода расположенного между лопатками выше расчётного сечения;  - ширина обода в расчётном сечении;
- ширина обода в расчётном сечении;  - толщина перемычки обода в расчётном сечении; е – высота зуба хвостовика.
- толщина перемычки обода в расчётном сечении; е – высота зуба хвостовика. . (1.87)
. (1.87)

 (число оборотов в секунду) получает за один оборот один импульс, то за одну секунду будет подвержена
(число оборотов в секунду) получает за один оборот один импульс, то за одну секунду будет подвержена  -
-  импульсам.
импульсам. . (2.1)
. (2.1) , (2.2)
, (2.2) - постоянное среднее давление;
- постоянное среднее давление;  - амплитуды сил от первой, второй и
- амплитуды сил от первой, второй и 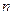 - ой гармоники;
- ой гармоники;  - угол, отсчитываемый от произвольной точки корпуса;
- угол, отсчитываемый от произвольной точки корпуса;  - фазовые углы.
- фазовые углы.
 =
=  (2.3)
(2.3) , (2.4)
, (2.4) - длина лопатки;
- длина лопатки;  - момент сопротивления в корневом сечении;
- момент сопротивления в корневом сечении; 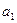 - амплитуда первой гармоники (принимается 0.03…0,05 от давления входа перед лопаткой);
- амплитуда первой гармоники (принимается 0.03…0,05 от давления входа перед лопаткой);  - коэффициент определяется формой колебаний (для первой формы
- коэффициент определяется формой колебаний (для первой формы  );
); 
 (2.5)
(2.5) (2.6)
(2.6)
 (2.7)
(2.7) то и напряжения
то и напряжения  ,
, напряжение от статических газовых сил.
напряжение от статических газовых сил. то, подставляя значения
то, подставляя значения  в уравнение (2.7), получим
в уравнение (2.7), получим
 - от статических газовых сил. Проведенный анализ является оценочным и показывает, что напряжения изгиба в пластине с жесткой заделкой от переменной силой являются весьма существенными и значительно превосходят напряжения от статической нагрузки.
- от статических газовых сил. Проведенный анализ является оценочным и показывает, что напряжения изгиба в пластине с жесткой заделкой от переменной силой являются весьма существенными и значительно превосходят напряжения от статической нагрузки.

 от места заделки малый элемент dx и заменим воздействие отброшенных частей поперечными силами
от места заделки малый элемент dx и заменим воздействие отброшенных частей поперечными силами 
 , или
, или  (2.8)
(2.8) - плотность материала лопатки; F- площадь рассматриваемого поперечного сечения лопатки.
- плотность материала лопатки; F- площадь рассматриваемого поперечного сечения лопатки.
 (2.9)
(2.9)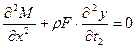 . (2.10)
. (2.10) . (2.11)
. (2.11) (2.12)
(2.12) тогда (2.12) запишется
тогда (2.12) запишется (2.13)
(2.13)
 и координаты
и координаты 
 (2.15)
(2.15) (2.16)
(2.16) (2.17)
(2.17) и
и  составим из равенства (2.17) два обыкновенных дифференциальных уравнения
составим из равенства (2.17) два обыкновенных дифференциальных уравнения (2.18)
(2.18)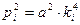 (2.19)
(2.19) (2.20)
(2.20) .
. (2.21)
(2.21) (2.22)
(2.22) (2.23)
(2.23) (2.24)
(2.24) . (2.25)
. (2.25) и
и  связаны с амплитудой и фазой колебаний и определяются по граничным условиям.
связаны с амплитудой и фазой колебаний и определяются по граничным условиям. связаны соотношением
связаны соотношением (2.26)
(2.26)

 (2.27)
(2.27)

 (2.28)
(2.28)
 (2.29)
(2.29)

 ;
; 

 (2.30)
(2.30) (2.31)
(2.31) и
и  не равны нулям, то определитель системы равен нулю:
не равны нулям, то определитель системы равен нулю: (2.32)
(2.32)

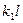 =1.875, получим первую частоту свободных колебаний
=1.875, получим первую частоту свободных колебаний (2.34)
(2.34) (2.35)
(2.35) и учитывая соотношения (2.30) имеем
и учитывая соотношения (2.30) имеем (2.36)
(2.36) (2.37)
(2.37) (2.38)
(2.38)
 -масса
-масса  - площадь и момент инерции
- площадь и момент инерции  (2.39)
(2.39) и амплитудой
и амплитудой  по гармоническому закону
по гармоническому закону (2.40)
(2.40) . (2.41)
. (2.41) в уравнение (2.41) и, проведя дифференцирование, получим
в уравнение (2.41) и, проведя дифференцирование, получим . (2.42)
. (2.42) , (2.43)
, (2.43) - коэффициент влияния представляющий собой прогиб в k точке, от единичной силы, приложенной в точке i.
- коэффициент влияния представляющий собой прогиб в k точке, от единичной силы, приложенной в точке i.  (2.44)
(2.44) (2.45)
(2.45) , удовлетворяющие уравнению (2.45) и есть искомые.
, удовлетворяющие уравнению (2.45) и есть искомые. , (2.46)
, (2.46) ;
;  - коэффициенты, зависящие от массовых и упругих характеристик лопатки, в частности
- коэффициенты, зависящие от массовых и упругих характеристик лопатки, в частности (2.47)
(2.47) , (2.48)
, (2.48) - корни уравнения (2.46).
- корни уравнения (2.46). (2.49)
(2.49) (2.50)
(2.50) (2.51)
(2.51) определяются через интеграл Мора
определяются через интеграл Мора , (2.52)
, (2.52) - момент от единичной силы, приложенный в точке
- момент от единичной силы, приложенный в точке  - момент инерции сечения лопатки расположенного на расстоянии Х от места заделки.
- момент инерции сечения лопатки расположенного на расстоянии Х от места заделки.

 тогда
тогда (2.53)
(2.53) , (2.54)
, (2.54) (2.55)
(2.55) .
. . Повышение температуры снижает Е и, следовательно, частоту собственных колебаний лопатки по соотношению
. Повышение температуры снижает Е и, следовательно, частоту собственных колебаний лопатки по соотношению .
. . Для материалов, из которых изготавливаются лопатки, это отношение меняется незначительно. Так частоты собственных колебаний стальных лопаток всего на 5…7%, а титановых на 6…8% больше чем изготовленной из алюминия при тех же размерах. Однако усталостная прочность у лопаток из алюминия ниже в 4…5 раз.
. Для материалов, из которых изготавливаются лопатки, это отношение меняется незначительно. Так частоты собственных колебаний стальных лопаток всего на 5…7%, а титановых на 6…8% больше чем изготовленной из алюминия при тех же размерах. Однако усталостная прочность у лопаток из алюминия ниже в 4…5 раз. приводит к снижению первой собственной частоты колебаний лопатки пропорционально корню квадратному из отношения моментов
приводит к снижению первой собственной частоты колебаний лопатки пропорционально корню квадратному из отношения моментов
 ), при неизменной площади корневого сечения, повышает частоту первой формы изгибных колебаний.
), при неизменной площади корневого сечения, повышает частоту первой формы изгибных колебаний. ), при постоянной площади корневого сечения, приводит к снижению частоты собственных колебаний лопатки.
), при постоянной площади корневого сечения, приводит к снижению частоты собственных колебаний лопатки.
 и кинетической
и кинетической  (2.56)
(2.56)
 , при этом центробежная сила совершает работу. Пренебрегаем ввиду малости окружной составляющей центробежной силы
, при этом центробежная сила совершает работу. Пренебрегаем ввиду малости окружной составляющей центробежной силы  , получим максимальную работу центробежных сил при максимальном прогибе
, получим максимальную работу центробежных сил при максимальном прогибе (2.57)
(2.57) , а
, а  ,
,  (2.58)
(2.58) (2.59)
(2.59)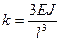 - коэффициент жесткости.
- коэффициент жесткости. из равенства (2.59)в зависимость (2.58), получим
из равенства (2.59)в зависимость (2.58), получим . (2.60)
. (2.60) (2.61)
(2.61) (2.62)
(2.62) - круговая частота лопатки, находящейся в поле центробежных сил.
- круговая частота лопатки, находящейся в поле центробежных сил. (2.63)
(2.63) (2.64)
(2.64) (2.65)
(2.65) (2.66)
(2.66) и учитывая, что
и учитывая, что 
 (2.67)
(2.67)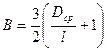 ,
, , (2.68)
, (2.68) круговая частота колебаний неподвижной лопатки
круговая частота колебаний неподвижной лопатки


 определяется частотой собственных колебаний при неподвижном роторе
определяется частотой собственных колебаний при неподвижном роторе  и частоты колебаний идеально гибкой лопатки находящейся в поле центробежных сил
и частоты колебаний идеально гибкой лопатки находящейся в поле центробежных сил (2.69)
(2.69)


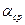 - средний по длине угол закрутки лопатки,
- средний по длине угол закрутки лопатки,  - средний радиус лопатки;
- средний радиус лопатки;  ,
, , (2.70)
, (2.70) , (2.71)
, (2.71)
 - число оборотов ротора в с
- число оборотов ротора в с 


