
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт на прочность дисков роторов гтдСодержание книги
Поиск на нашем сайте
Диски роторов ГТД, работают при высоких скоростях вращения, при высоких температурах (газовые турбины) и её градиенте вдоль радиуса, что обуславливает появления в них значительных нагрузок. На рабочем установившемся режиме в диске возникают следующие напряжения: - напряжения растяжения от центробежных сил самого диска, а также от центробежных сил масс лопаток установленных на ободе диска; - температурные напряжения, обусловленные изменением температуры, как по радиусу, так и по толщине; - напряжения изгиба от газовых сил, действующих на лопатки от газовых сил, а также от центробежных сил масс лопаток и диска в случае отклонения центров тяжести этих масс от срединной плоскости диска. Кроме того, из-за высоких температур, снижается механическая прочность материала диска. Существует два основных подхода к расчёту дисков на прочность: 1. Анализ прочности диска известного профиля. 2. Определение оптимального профиля диска с учетом ограничений на его характеристики прочности. По первому подходу проверяются его прочностные свойства по двум критериям: - по запасу прочности; - по несущей способности (разрушающим оборотам). При невыполнении одного из двух критериев необходимо изменять геометрию диска или применять другой материал. По второму подходу для выполнения расчетов необходимы пакеты программ и уточнение профиля диска по конструктивным соображениям. Расчёт прочности диска связан с определением напряжённого состояния в любой точке диска и для диска любой конструктивной схемы является очень сложной задачей. Рассмотрим упрощенную расчетную схему по определению напряжений в диске. Примем следующие допущения: - материал диска упругий; - диск тонкий (толщина диска много меньше наружного радиуса); - диск симметричен относительно своей срединной плоскости; - напряжения изгиба и кручения не учитываются; - температура изменяется только по радиусу; - напряжения от лопаток на внешнем диаметре и от запрессовки диска на вал распределены равномерно по толщине и окружности. С учётом допущений можно считать, что в диске возникают напряжения направленные по нормалям к кольцевому сечению Исходными для расчета напряжений в диске являются уравнения равновесия и уравнения совместных деформаций, выраженные в напряжениях. Уравнения равновесия. Рассмотрим условия равновесия сил действующих на бесконечно малый элемент диска заключенный между двумя концентрическими поверхностями, отстоящими на расстоянии
Рис. 6.1. Расчетная схема диска на прочность от центробежных сил При вращении диска угловой скоростью
где От действия центробежной силы на концентрических и радиальных поверхностях выделенного элемента возникают нормальные напряжения: - на внутреннем цилиндрическом сечении, расположенном на радиусе - на внешнем цилиндрическом сечении, расположенном на радиусе - на радиальных поверхностях, ввиду симметричности элемента тангенциальные напряжения Составим уравнения сил на поверхностях выделенного элемента от нормальных напряжений. На внутренней цилиндрической поверхности
На внешней цилиндрической поверхности
На радиальных поверхностях
Спроецируем все силы на вертикальную ось и запишем уравнение равновесия сил действующих на выделенный элемент
Подставляя выражения (6.1 … 6.4) и учитывая, что ввиду малости
В уравнении (5.6) при известном законе изменения толщины диска по радиусу содержится два неизвестных Второе уравнения получим, связав
где Относительные удлинения
Дифференцируя соотношение (6.9), получим
С учетом (6.7) уравнение (6.10) запишется
Подставим в уравнение (6.11) выражения для
Уравнения (6.6) и (6.12) позволяют найти искомые напряжения
Рис.6.2. Формы профилей дисков: а – постоянной толщины; б -конический; в – гиперболический; г– равного сопротивления
Если нет аналитической зависимости изменения толщины диска по радиусу, то задача решается приближёнными методами.
6.1. РАСЧЕТ ДИСКА ПОСТОЯННОЙ ТОЛЩИНЫ
Для диска постоянной толщины h= const. Запишем выражение (6.6) с учетом h= const вследующем виде:
Дифференцируя, по r найдем
Подставим выражения 6.13 и 6.14 в формулу 6.12 получим
Проинтегрируем выражение (6.15) дважды, получим
где А1 и А2 – постоянные интегрирования; ri – внутренний радиус диска (для диска сплошного, без центрального отверстия ri =0). Напряжения
Постоянные А1 и А2 определяются из граничных условий. На наружном радиусе диска В сплошном диске r=0, А2=0 радиальные напряжения
Рис. 6.3. Распределения напряжений по радиусу равномерно нагретого вращающегося диска: а - диск сплошной; б - диск с отверстием;
В диске с внутренним отверстием Величина напряжения С учётом граничных условий формулы для расчета распределения напряжений по радиусу равномерно нагретого диска запишутся
(6.18)
Напряжения Контурная нагрузка на периферии сплошного диска увеличивает на величину Напряжения от инерционных сил массы диска увеличиваются с ростом окружной скорости периферии диска Изменение относительных напряжений по радиусу вращающегося с угловой скоростью В неравномерно нагретом неподвижном диске рис.6.4 относительные напряжения на контуре центрального отверстия также примерно в два раза превышают напряжения в центре сплошного диска. Изменение напряжений по радиусу диска рис.6.4 построены для параболического закона распределения температуры по радиусу
При При выключении двигателя обод диска турбины остывает быстрее, чем центр, при этом
6.2 РАСЧЕТ РАВНОПРОЧНОГО ДИСКА
Равнопрочным называется диск в котором во всех точках радиальные напряжения равны тангенциальным и постоянны по радиусу, т.е.
При данном определении уравнение (5.6) можно записать
или
Интегрируя уравнение (6.20) в пределах от текущего радиуса
Из формулы (6.22) выразим
Толщина диска
Центробежная сила масс
Центробежная сила от массы бандажа
где Центробежная сила от масс замковой части
где
6.3. РАСЧЕТ НА ПРОЧНОСТЬ ВРАЩАЮЩЕГОСЯ ДИСКА ПРОИЗВОЛЬНОГО ПРОФИЛЯ
Представим уравнения равновесия и совместных деформаций в следующем виде
Разобьём диск рядом концентрических кольцевых сечений от 0 до к (рис. 6.5).
Рис.6.5. К расчету диска методом конечных разностей
Заменим дифференциалы в системе (6.29) конечными разностями:
где Подставим уравнения (6.29) в уравнения (6.28) принимая для величин проведем преобразования
Обозначим:
получим
Выразим напряжения в каждом сечении через напряжения в нулевом сечении. Для диска с центральным отверстием нулевое сечение расположено на радиусе отверстия, причем для напрессованного диска на вал радиальные и тангенциальные напряжения равны напряжениям посадки
Для сплошного диска нулевое сечение проводится вблизи оси вращения, где также принимается Рассмотрим расчет напряжений
где
Для второго сечения
Подставим в него уравнения (6.34)
где
Очевидно, что для любого
где
В нулевом сечении формулы (6.36) запишутся: - диск, сплошной:
откуда
- диск с отверстием:
откуда
Неизвестные напряжения в нулевом сечении диска
откуда
Порядок расчёта 1. По геометрическим параметрам разбиения диска и режимным параметрам работы по зависимостям (6.31) рассчитываются 2. Последовательным расчётом по формулам (6.37) определяются 3. По формуле (6.39) рассчитывается 4. По зависимостям (6.36) определяется Точность расчёта зависит от числа участков разбиений и их расположения. Обычно назначается не менее 10 сечений. Радиус нулевого сечения для сплошного диска назначается равным (0.03…0.05) Rн. В местах с резким изменением толщины диска сечения выбираются на меньшем расстоянии друг от друга. Возможно назначения двух сечений на одном радиусе с различной толщиной диска. Расчёт выполняется в виде таблицы. По рассчитанным радиальным и тангенциальным напряжениям определяются эквивалентные напряжения
Определяется коэффициенты запасов прочности по радиусу диска
Типовые зависимости распределения напряжений по радиусу диска и коэффициенты запасов прочности с учетом изменения температуры см. рис.6.6
Рис.6.6. Распределение напряжений по радиусу диска
В качестве предельных допустимых напряжений 6.4. Контрольные вопросы 1. Составьте схему расчета диска произвольного профиля. 2. Основные допущения расчетной схемы. 3. Назовите нагрузки, действующие на диски компрессоров и газовых турбин. 4. Почему при расчете прочности дисков газовых турбин необходимо учитывать температуру и её изменение по радиусу? 5. Какие напряжения возникают во вращающемся нагретом диске? 6. Каким образом влияет профиль диска на распределения напряжений? 7. Какой диск называется равнопрочным? 8. Обоснуйте влияние на напряжения в диске контурной нагрузке от лопаток. 9. Как изменяются напряжения в диске при выполнении в нем центрального отверстия? 10. Как влияет величина натяга при запрессовке диска на вал? 11.Обоснуйте необходимость при определении напряжений учитывать материал дисков? 12. Диск, какой формы имеет минимальную массу и почему? КОЛЕБАНИЯ ДИСКОВ Диски роторов являются одними из наиболее нагруженных элементов авиадвигателей. При работе в них возникают напряжения от центробежных и осевых сил, температурные напряжения, напряжения от газодинамических сил и т.д. Эти нагрузки зачастую переменны, что вызывает колебания дисков, а при определенных частотах и амплитудах ведут к их разрушению, в итоге все это приводит к катастрофическим последствиям. Формы колебаний дисков (рис.7.1) могут быть: без узловых линий ( Каждой форме колебаний соответствует своя частота. Чем больше число узлов колебаний, тем выше частота колебаний. Наиболее опасными являются «веерные» колебания с двумя и более диаметрами.
Рис.7.1. Формы колебаний дисков:
Волнообразные колебания невращающихся дисков Рассмотрим волнообразные колебания диска с числом узловых диаметров равным двум (рис.7.2).
Рис.7.2. Схема веерных колебаний с двумя узловыми диаметрами
Уравнения прогибов точек диска при колебаниях в полярной системе координат запишется
где Перемещение точек, лежащих на радиусе Каждой форме собственных колебаний соответствует строго определенная частота колебаний. Для простых круглых пластин частота может быть подсчитана по формуле
где ρ - массовая плотность материала диска; δ - толщина диска;
В таблицах 7.1 и 7.2 приведены значения коэффициентов частоты для условий закрепления пластины по внешнему и внутреннему диаметрам. Закрепление пластины на внешнем диаметре таблица 7.1
Закрепление пластины по центральному отверстию таблица7.2
Формула (7.2) и таблицы коэффициентов позволяют проанализировать соотношения собственных частот различных форм колебаний и зависимость от основных размеров, материала и условий закрепления. Формы собственных колебаний рабочих колес компрессоров и газовых турбин ГТД аналогичны формам колебаний простых пластин с учетом реальных факторов. Представим произведение косинусов (7.1) в виде суммы
тогда
Каждое слагаемое формулы (7.4) представляет собой колебание точек диска, сдвинутые по фазе на угол, пропорциональный координате
Рис. 7.3. Расположение бегущих на диске волн: а- волна в сторону вращения; б – волна во встречном направлении
Каждое из слагаемых по отдельности удовлетворяет общему уравнению колебаний диска, поэтому их можно рассматривать как независимые решения. То есть фазовые волны могут существовать на диске независимо друг от друга. Для любого узлового диаметра выполняется условие
где
знак плюс относится к волне, бегущей вперед, а знак минус - к волне, бегущей навстречу. Из формулы видно, что угол Продифференцируем выражение (7.6), получим скорость перемещения узловых диаметров по диску
Волны бегут в противоположные стороны с одинаковой скоростью, пропорциональной частоте собственных колебаний. Правило движения фазовых волн сохраняется и на вращающемся с угловой скоростью
Из (7.8) очевидно, что абсолютные угловые скорости прямых и обратных и волн различны. Абсолютная угловая скорость обратной волны Угловые скорости вращения, при которых форма колебаний остается неподвижной относительно неподвижной системы координат называется критической и определяется
На критических скоростях вращения возникает явление резонанса, диск теряет устойчивость. Под воздействием неосесимметричного статического давления на боковую поверхность диска или лопатки появляются большие деформации и напряжения изгиба диска, что может привести к задеванию о статор, обрыву лопаток и разрушению диска. Для исключения опасных резонансных явлений в зоне рабочих угловых скоростей вращения роторов не рекомендуется допускать существования критических угловых скоростей дисков, особенно с числом узловых диаметров Для определения опасных оборотов на графике строятся зависимости собственных частот от угловых скоростей вращения ротора
Рис.7.4. Определение критических скоростей вращения рабочих колес
Рекомендуется на двигателях иметь запас по критическим скоростям вращения
В зависимости от числа узловых диаметров
Отстроиться от резонансных режимов можно изменением собственной частоты колебаний дисков или изменением порядка гармоник возмущающих сил. Проведем анализ влияния различных факторов на собственные частоты. Собственные частоты колебаний диска повышаются до 1.5…2 раз с увеличение коничности или гиперболичности полотна диска. Широкий обод на периферии диска увеличивает его изгибную жесткость, что может увеличить частоту собственных колебаний на 10…15%. Лопатки, расположенные на периферии диска снижают собственные частоты колебаний дисков. Причем снижение частот определяется как соотношением масс лопаток
Рис.7.5. Влияние массы лопаток на частоту собственных колебаний рабочих колес
Существенное влияние на частоты собственных колебаний оказывает угловая скорость вращения рабочего колеса так как центробежные силы от масс диска стремятся вернуть отклоняющиеся части диска в состояние равновесия, что приводит к увеличению частоты собственных колебаний (рис.7.6). Повышение частот собственных колебаний рабочих колес от угловой скорости вращения ротора зависит от геометрической формы рабочего колеса и лопаток, соотношения их масс и жесткостей и может достигать двукратного значения. Расчет собственных частот колебаний рабочих колес производится по энергетическому методу Рэлея. Количественная зависимость может быть представлена формулой
где Температура дисков влияет на собственные частоты колебаний за счет изменения модуля упругости материала. Кроме этого при рабочих режимах температура дисков существенно изменяется по радиусу, что приводит к возникновению больших напряжений сжатия на периферии и напряжений растяжения в центре. При этом частоты собственных колебаний рабочих колес снижаются, что может быть определено по методу Рэлея.
Рис.7.6.Влияние скорости вращения на частоту собственных колебаний диска
Расчет собственной частоты колебаний диска с лопатками с учетом изменения температуры для формы колебаний с двумя узловыми диаметрами можно оценить по формуле
где Закон изменения температуры по радиусу диска принят кубическим
При этом снижение частот собственных колебаний, может происходить на 20…25%, увеличиваясь для тонких дисков большого диаметра. В реальном двигателе на диск одновременно воздействует угловая скорость и температура, поэтому при малых угловых скоростях основное влияние оказывают центробежные силы лопаток, а с ростом скорости вращения ротора и температуры – температурный фактор. Поэтому для одних форм ко
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 3210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.123.61 (0.015 с.) |

 и радиальному сечению
и радиальному сечению  диска.
диска. друг от друга и на расстоянии
друг от друга и на расстоянии  от оси вращения и двумя радиальными поверхностями, проходящими через ось вращения под углом
от оси вращения и двумя радиальными поверхностями, проходящими через ось вращения под углом  (рис.6.1).
(рис.6.1).

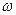 на выделенный элемент действует центробежная сила
на выделенный элемент действует центробежная сила  , приложенная в центре тяжести, которая определяется по зависимости
, приложенная в центре тяжести, которая определяется по зависимости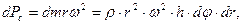 (6. 1)
(6. 1)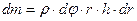 - масса выделенного элемента; составляющими порядка
- масса выделенного элемента; составляющими порядка 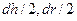 и др. пренебрегаем ввиду их малости
и др. пренебрегаем ввиду их малости ;
;
 напряжение
напряжение  и радиальная сила, направленная от центра вращения
и радиальная сила, направленная от центра вращения  ;
; направлены по нормали к поверхности.
направлены по нормали к поверхности.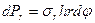 (6.2)
(6.2) (6.3)
(6.3) (6.4)
(6.4)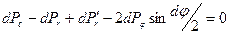 . (6.5)
. (6.5) получим уравнение равновесия в напряжениях
получим уравнение равновесия в напряжениях (6.6)
(6.6) .
. с деформациями по закону Гука с учетом температурных деформаций. Относительные удлинения волокон в радиальном
с деформациями по закону Гука с учетом температурных деформаций. Относительные удлинения волокон в радиальном  и окружном
и окружном 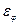 направлениях определятся
направлениях определятся , (6.7)
, (6.7) -коэффициент Пуассона;
-коэффициент Пуассона;  - коэффициент температурного линейного расширения материала диска;
- коэффициент температурного линейного расширения материала диска;  - температура диска на радиусе
- температура диска на радиусе  , (6.8)
, (6.8)  или
или 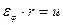 (6.9)
(6.9) (6.10)
(6.10)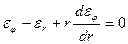 (6.11)
(6.11) (6.12)
(6.12) и их изменения по радиусу. Точное решение этих уравнений возможно только для частных случаев профилей дисков, например диск постоянной толщины, конический или параболический закон изменения профиля диска по радиусу, диск равного сопротивления (Рис. 6.2).
и их изменения по радиусу. Точное решение этих уравнений возможно только для частных случаев профилей дисков, например диск постоянной толщины, конический или параболический закон изменения профиля диска по радиусу, диск равного сопротивления (Рис. 6.2).
 (6.13)
(6.13) (6.14)
(6.14) (6.15)
(6.15)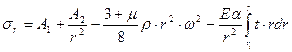 , (6.16)
, (6.16) (6.17)
(6.17)
 радиальные напряжения
радиальные напряжения  при их наличии.
при их наличии. а б
а б ;
; 
 радиальные напряжения
радиальные напряжения  , при посадке диска на вал с натягом.
, при посадке диска на вал с натягом.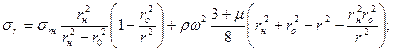

 и плотности материала
и плотности материала  .
. , (6.19)
, (6.19) - разность температур в центре и на периферии диска.
- разность температур в центре и на периферии диска. Рис.6.4 Распределения напряжений по радиусу неравномерно нагретого невращающегося диска: а - диск сплошной; б- диск с отверстием;
Рис.6.4 Распределения напряжений по радиусу неравномерно нагретого невращающегося диска: а - диск сплошной; б- диск с отверстием; 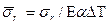 ;
; 
 , на периферии диска возникают сжимающие (отрицательные) тангенциальные напряжения, обусловленные стремлением диска на этих радиусах расшириться больше, чем это допускают более холодные внутренние участки диска.
, на периферии диска возникают сжимающие (отрицательные) тангенциальные напряжения, обусловленные стремлением диска на этих радиусах расшириться больше, чем это допускают более холодные внутренние участки диска. становится отрицательной, напряжения
становится отрицательной, напряжения  .
. , (6.20)
, (6.20) (6.21)
(6.21) получим
получим
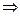
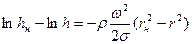 (6.22)
(6.22)
 (6.23)
(6.23) на внешнем радиусе
на внешнем радиусе 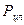 , центробежной силы массы бандажа
, центробежной силы массы бандажа  и центробежной силы массы замковой части обода диска
и центробежной силы массы замковой части обода диска 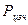 :
: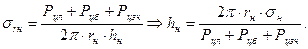 (6.24)
(6.24)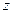 лопаток размещенных на ободе диска определяется
лопаток размещенных на ободе диска определяется , (6.25)
, (6.25) - масса профильной части одной лопатки;
- масса профильной части одной лопатки; 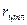 - расстояние от оси вращения диска до центра тяжести масс лопатки.
- расстояние от оси вращения диска до центра тяжести масс лопатки. (6.26)
(6.26) - масса бандажа (
- масса бандажа ( - радиус бандажа, толщина бандажа и ширина бандажа соответственно);
- радиус бандажа, толщина бандажа и ширина бандажа соответственно);  расстояние от оси вращения до центра тяжести масс бандажа.
расстояние от оси вращения до центра тяжести масс бандажа. , (6.27)
, (6.27) - масса замковой части (
- масса замковой части ( - радиус корневого сечения лопаток, радиус и ширина наружной поверхности рассчитываемого диска соответственно);
- радиус корневого сечения лопаток, радиус и ширина наружной поверхности рассчитываемого диска соответственно);  - расстояние от оси вращения до центра тяжести масс замковой части.
- расстояние от оси вращения до центра тяжести масс замковой части. (6.28)
(6.28)
 (6.29)
(6.29) номер кольцевого сечения диска.
номер кольцевого сечения диска. их значения в сечении
их значения в сечении 
 (6.30)
(6.30) (6.31)
(6.31) (6.32)
(6.32) .
. в сечениях сплошного диска, используя уравнения (6.32)
в сечениях сплошного диска, используя уравнения (6.32)

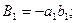

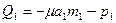 .
. (6.34)
(6.34) (6.35)
(6.35)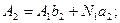
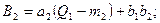

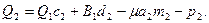
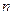 -го сечения можно записать
-го сечения можно записать , (6.36)
, (6.36)


 (6.37)
(6.37)




 определяются по напряжению в периферийном сечении диска, которое рассчитывается по зависимостям (6.34).
определяются по напряжению в периферийном сечении диска, которое рассчитывается по зависимостям (6.34). (6.38)
(6.38) (6.39)
(6.39)

 .
. (6.40)
(6.40) (6.41)
(6.41)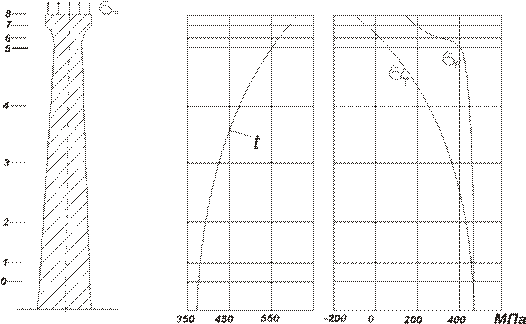
 принимается для турбин предел длительной прочности материала
принимается для турбин предел длительной прочности материала  , для дисков компрессоров предел текучести материала
, для дисков компрессоров предел текучести материала  или
или 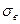 .
.
 ) - зонтичные; с узловыми диаметрами - волнообразные («веерные») (s=0; i=2,3,4 и т.д .); с узловыми окружностями - «осесимметричные» (i=0; s =0,1,2,3 и т.д.);комбинация узловых окружностей и диаметров (
) - зонтичные; с узловыми диаметрами - волнообразные («веерные») (s=0; i=2,3,4 и т.д .); с узловыми окружностями - «осесимметричные» (i=0; s =0,1,2,3 и т.д.);комбинация узловых окружностей и диаметров (
 ).
).
 - число узловых диаметров;
- число узловых диаметров; 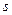 - число узловых окружностей; 1 – узловые диаметры; 2 – узловые окружности
- число узловых окружностей; 1 – узловые диаметры; 2 – узловые окружности
 (7.1)
(7.1) - функция радиуса, определяющая форму колебаний диска по радиусу;
- функция радиуса, определяющая форму колебаний диска по радиусу;  - полярный угол, отсчитываемый от одного из узловых диаметров;
- полярный угол, отсчитываемый от одного из узловых диаметров;  - круговая частота свободных колебаний диска;
- круговая частота свободных колебаний диска;  (7.2)
(7.2) - наружный радиус диска; μ - коэффициент Пуассона;
- наружный радиус диска; μ - коэффициент Пуассона; - цилиндрическая жесткость;
- цилиндрическая жесткость; - коэффициент частоты, определяемый формой колебаний и условиями закрепления.
- коэффициент частоты, определяемый формой колебаний и условиями закрепления. (7.3)
(7.3)
 (7.4)
(7.4)
 При этом условии должно выполняться равенство
При этом условии должно выполняться равенство (7.5)
(7.5) - угол, определяющий место расположения узлового диаметра рис. 7.3.
- угол, определяющий место расположения узлового диаметра рис. 7.3. (7.6)
(7.6) (7.7)
(7.7) диске. С учетом увеличения собственных частот вследствие вращения диска, абсолютные скорости фазовых волн
диске. С учетом увеличения собственных частот вследствие вращения диска, абсолютные скорости фазовых волн  относительно неподвижной системы координат, определяются
относительно неподвижной системы координат, определяются . (7.8)
. (7.8) становится равной нулю. При этом сама форма колебаний относительно неподвижных осей оказывается неподвижной, а все точки вращающегося диска, следуя по этой форме, совершают поперечные колебания.
становится равной нулю. При этом сама форма колебаний относительно неподвижных осей оказывается неподвижной, а все точки вращающегося диска, следуя по этой форме, совершают поперечные колебания. . (7.9)
. (7.9)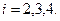 Для определения критических угловых скоростей необходимо знать собственные частоты колебаний диска как функции угловой скорости.
Для определения критических угловых скоростей необходимо знать собственные частоты колебаний диска как функции угловой скорости.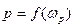 и из начала координат проводятся прямые
и из начала координат проводятся прямые  . Точки пересечения прямых определяют критические угловые скорости вращения дисков (рис.7.4).
. Точки пересечения прямых определяют критические угловые скорости вращения дисков (рис.7.4).
 (7.10)
(7.10)





 и массы диска
и массы диска  , так и соотношением длинны лопатки и радиуса диска. Типовые зависимости собственных частот колебаний рабочих колес с учетом этих факторов приведены на рис.7.5.
, так и соотношением длинны лопатки и радиуса диска. Типовые зависимости собственных частот колебаний рабочих колес с учетом этих факторов приведены на рис.7.5.
 (7.11)
(7.11) - коэффициент влияния угловой скорости.
- коэффициент влияния угловой скорости.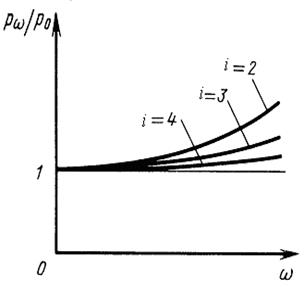
 (7.12)
(7.12)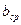 - средняя ширина диска;
- средняя ширина диска; 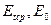 - модули упругости материала на среднем диаметре при температуре t и
- модули упругости материала на среднем диаметре при температуре t и  ;
;  - разность температур на внешнем контуре и центре диска.
- разность температур на внешнем контуре и центре диска.



