
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охарактеризуйте роль и виды модуляции в системах связи.Содержание книги
Поиск на нашем сайте
а) роль модуляции в системах связи Все системы связи основаны на передаче различных сигналов из одного пункта в другой. Эта задача встречается в радио и телевизионном вещаний, связи по телефонным линиям на большие расстояния, спутниковой связи, системах телеуправления, телеметрии и т. д. Сигналы из одного пункта в другой передаются по каналу, который может быть парой проводов (например, телефонный) или просто открытым пространством, в которое излучаются сигналы, несущие полезную информацию (радио и телевизионное вещание, спутниковая связь и т. п.). Каждый из передаваемых сигналов обычно имеет малую ширину спектра по сравнению с полосой пропускания канала. Поэтому передавать лишь один сигнал по каналу невыгодно, так как емкость канала будет использоваться весьма незначительно. Вместе с тем, непосредственная передача по каналу одновременно нескольких сигналов привела бы к наложению этих сигналов и выделение их на приемной стороне оказалось бы невозможным. Указанная трудность преодолевается посредством использования частотного уплотнения. Если сдвинуть частотные спектры различных сигналов так, чтобы они занимали неперекрывающиеся частотные полосы, можно передавать одновременно большое число сигналов по одному каналу. В предыдущих лекциях упоминалось, что сдвиг частотного спектра выполняется посредством модуляции, т. е. умножения сигнала на синусоидальное колебание. Спектр каждого сигнала сдвигается так, чтобы перекрытие спектров соседних сигналов отсутствовало. На приемной стороне сигналы разделяются частотными фильтрами. Однако, выделенный фильтром сигнал, еще не есть исходное сообщение, так как его спектр сдвинут по частоте. Для того чтобы получить исходное сообщение, необходимо выполнить обратный перенос спектра сигнала. В системах связи с излучением электромагнитных волн модуляция служит и для другой цели. В теории электромагнитных волн показывается, что эффективное излучение возможно лишь в том случае, если размер антенны составляет не менее одной десятой длины волны излучаемого сигнала. Речевой сигнал имеет наивысшую частоту около 10 кГц, что соответствует наименьшей длине волны 30 000 м. Таким образом, для излучения электромагнитных волн, соответствующих речевому сигналу, потребовалась бы антенна длиной в несколько километров, что конечно, непрактично. Модуляция сдвигает спектр сигнала на любую требуемую частоту, облегчая, таким образом, задачу излучения сигнала. Обычно несущая частота сигнала весьма высока (в системах радиовещания выше 150 кГц). Итак, модуляция не только решает задачу одновременной передачи нескольких сигналов, но и обеспечивает возможность их эффективного излучения. б) виды модуляции в системах связи Амплитудная модуляция (АМ) При обычной амплитудной модуляции мгновенное значение огибающей изменяется около некоторого среднего уровня по закону, связанному линейной зависимостью с модулирующей функцией. Отличительной особенностью AM является то, что огибающая модулированного сигнала в точности повторяет изменения модулирующего колебания. Схематически AM сигнал можно рассматривать как результат перемножения синусоидальной несущей и сигнала, образованного суммой модулирующей функции и некоторой постоянной величины. Результирующий AM сигнал eам (t) = [1+g (t)] cos (2πfc t). (1) Обычно AM сигнал записывается в виде eам (t) = [1+ ma g (t)] cos (2πfc t). (2) где та называется индексом модуляции, причем на та и модулирующую функцию накладываются ограничения: | g (t) | Если условия (3) нарушаются, то возникает перемодуляция, при которой появляются искажения огибающей, обусловленные тем, что она не может принимать отрицательных значений. Спектр g(t) не выходит за пределы области | f |
Рис.1 Формирование обычного АМ сигнала.
Спектр АМ сигнала содержит несущую и две боковые полосы, получающиеся смещением основного спектра в окрестность несущей, причем боковые полосы являются комплексно сопряженными зеркальными отображениями друг друга. Для передачи такого сигнала требуется полоса частот шириной 2 f.
Рис.2 Спектры амплитудно-модулированных сигналов. Анализ энергетических характеристик показывает, что средняя мощность несущей равна величине Pc = а мощность каждой боковой полосы Рвбп = Рнбп = отсюда полная мощность боковых полос Рбп = Рвбп + Рнбп = Для получения максимальной мощности информационных составляющих AM сигнала (боковых полос) положим та равным максимальному допустимому значению, т. е. единице. В этом случае имеем Рбп = Максимально возможная мощность боковых полос равна половине мощности несущей. Таким образом, на излучение информационных составляющих (боковых полос) сигнала идет не более одной трети общей мощности; остальная мощность расходуется на излучение несущей. Наиболее широко используемым методом демодуляции AM является амплитудное детектирование (рис. 3). Согласно рис. 3 принимаемый AM сигнал подается на диод, который не пропускает отрицательных значений сигнала, так что на его выходе получается положительная функция с ненулевым средним, значением. Поскольку информация содержится в низкочастотных колебаниях этого среднего значения (т. е. огибающей) относительно некоторого постоянного уровня, то, отделяя огибающую от высокочастотных колебаний фильтром нижних частот, можно воспроизвести исходную модулирующую функцию.
Рис.3 Амплитудное детектирование АМ сигналов
Заметим, что если огибающая принятого сигнала не точно повторяет изменения модулирующей функции, то информация будет воспроизведена с некоторыми искажениями. По этой причине, как было отмечено выше, максимально допустимое значение индекса модуляции равняется единице или 100%. Иногда 100-процентную модуляцию называют полной модуляцией. При перемодуляции индекс модуляции становится больше единицы (та>1) и огибающая сильно искажается относительно модулирующей функции. Среди разновидностей АМ существует метод балансной модуляции (БМ), отличающийся от АМ отсутствием в результирующем спектре сигнала несущего колебания, однако ширина полосы, которую занимает БМ сигнал остается той же, что и при обычной AM, так как в обоих случаях излучаются обе боковые полосы, каждая из которых полностью характеризует передаваемую информацию. Если найти возможность сузить занимаемую полосу частот, то это позволит разместить большее число каналов связи в данном диапазоне. Такая возможность существует в системах с видоизмененной AM, если в спектре излучаемого сигнала подавить несущую и одну боковую полосу. Такой вид модуляции известен под названием однополосная модуляция с подавлением несущей или просто однополосная модуляция (ОМ). В ОМ системах вся излучаемая мощность расходуется на передачу информации, которая вмещается в минимально возможную полосу частот. Так, при передаче одной боковой полосы экономится излучаемая мощность, лучше используется частотный диапазон. Теоретическое обоснование однополосной связи заключается в том, что как при БМ, так и при AM верхняя и нижняя боковые полосы содержат весь объем информации и, следовательно, для ее передачи достаточно лишь одной боковой полосы. Однако реализация ОМ связана со сложностью и дороговизной передатчиков и приемников, а также с проблемой совместимости, не позволяющей изменять вид модуляции без смены всей аппаратуры в существующих системах. В частности, поскольку формирование однополосного сигнала происходит в маломощных цепях, то для исключения искажений усилитель передатчика должен иметь достаточно линейную характеристику (что, в принципе, приводит к низкому коэффициенту полезного действия). В противоположность этому при БМ или AM существуют методы формирования сигнала непосредственно в мощных каскадах и, следовательно, в них могут использоваться более экономичные нелинейные усилители мощности. Можно также показать, что для модулирующих функций сложной формы отношение пиковой мощности к ее среднему значению в системах с ОМ оказывается более высоким, чем при БМ или AM, Кроме того, наличие несущей в спектре AM сигнала позволяет значительно упростить требования к приемнику и сделать его достаточно надежным. Несмотря на это, однополосная модуляция нашла широкое применение в многоканальных системах с частотным уплотнением. В последнее время связь на одной боковой полосе используется также на загруженных участках декаметрового и УКВ диапазонов с целью экономии занимаемой полосы частот. Угловая модуляция (УМ). Угловая модуляция — это общее название для двух тесно связанных между собой видов модуляции — частотной (ЧМ) и фазовой (ФМ). В системах с частотной модуляцией информация передается изменением мгновенной частоты несущего колебания, а при фазовой модуляции модулирующий сигнал непосредственно изменяет фазу несущей. Если амплитудная модуляция является, по существу, линейным процессом, при котором не возникают новые частоты, если не считать смещения спектра модулирующего сигнала в окрестность несущей частоты. При угловой модуляции также происходит перенос спектра, но, в отличие от AM, этот вид модуляции преобразует и форму спектра передаваемого сообщения.В большинстве случаев спектр излучаемого ЧМ или ФМ сигнала оказывается шире, чем спектр исходного модулирующего воздействия. Это свойство угловой модуляции создавать новые частотные составляющие характерно для всех форм нелинейных преобразований. Угловая модуляция обычно применяется, когда требуется обеспечить высокую верность приема передаваемого сообщения. Объясняется это тем, что системы с угловой модуляцией обладают повышенной по сравнению с AM устойчивостью к воздействию шумов и других видов помех. Известно, например, свойства ЧМ систем подавлять аддитивную шумовую помеху. Это значит, что при детектировании ЧМ существенно улучшается отношение сигнал/шум. Однако это преимущество достигается ценой ухудшения других параметров сигнала, в частности ценой увеличения занимаемой полосы частот. Частотная модуляция является, пожалуй, наиболее общим примером, который иллюстрирует методы повышения помехоустойчивости систем связи, основанные на расширении спектра сигнала. Однако, как и в других помехоустойчивых системах, увеличение отношения сигнал/шум имеет место только в случае, если на входе приемника оно выше некоторого критического уровня. Ниже этого уровня отношение сигнал/шум на выходе быстро падает, так что ЧМ оказывается даже менее выгодной, чем линейные системы, такие, например, как ОМ. Повышение выигрыша ЧМ путем расширения занимаемой полосы частот приводит, как правило, к повышению порога помехоустойчивости. Разработано, однако, несколько методов, позволяющих увеличить выигрыш ЧМ без изменения порога помехоустойчивости.
Для того чтобы записать аналитические выражения для сигналов с угловой модуляцией, необходимо найти закон изменения полной фазы θ (t) в зависимости от передаваемого сообщения. Пусть у несущего колебания: с0 (t) = cos [2πfсt+ под воздействием передаваемого сообщения изменяется либо частота fс, либо начальная фаза При фазовой модуляции в соответствии с модулирующим сигналом g(t) изменяется фаза несущего колебания в пределах +
где, как и при AM │ g(t)│ Наибольшее значение фазового сдвига θфм (t) = 2πfсt+
Следовательно, аналитическое выражение для сигнала с фазовой модуляцией будет: eфм(t)= cos [2πfсt+
При частотной модуляции в соответствии с модулирующим сигналом g(t) изменяется частота несущего колебания в пределах +
2πf(t)= 2πfсt +
Наибольшее значение частотного отклонения Полная фаза θ (t) при ЧМ равна θчм (t)=
следовательно, аналитическое выражение для сигнала с частотной модуляцией имеет вид: eчм(t)= cos [2πfсt+ Слагаемое При частотной модуляции модулирующая функция отображается скоростью изменения фазы (изменением мгновенной частоты относительно 2πfс); как изменяется сама фаза — значения с информационной точки зрения не имеет. Таким образом, при угловой модуляции изменение фазы несущего колебания по закону g(t) приводит к изменению мгновенной частоты по закону производной от g(t); изменение же мгновенной частоты по закону g(t) приводит к изменению фазы по закону интеграла от g(t). Это одно из основных положений теории угловой модуляции, определяющее связь между изменением частоты и фазы и подтверждающее общность, существующую между частотной и фазовой модуляцией. Рассмотрим однотональную угловую модуляцию, когда сигнал как при ФМ, так и при ЧМ можно записать так: eум(t)= cos [2πfсt+β sin2πFt] (6)
где β — так называемый индекс угловой модуляции;
βфм =
В формуле (6) начальная фаза под знаком косинуса опущена, как не имеющая принципиального значения. Таким образом, при однотональной угловой модуляции ФМ и ЧМ сигналы внешне практически неразличимы. Более того, если частота модуляции удовлетворяет соотношению: 2πFt= Временная диаграмма сигнала при однотональной угловой модуляции может быть представлена следующим образом.
Рис.1 Угловая модуляция: а — модулирующий низкочастотный сигнал; б — однотональный сигнал с угловой модуляцией
Различие между структурами ЧМ и ФМ сигналов проявляется, когда модулирующая функция имеет сложный спектральный состав, так как начинает сказываться то обстоятельство, что при ФМ изменение частоты — результат модуляции фазы, а при ЧМ изменение фазы — результат модуляции частоты. Исследование спектральных свойств сигналов с угловой модуляцией в математическом отношении существенно сложнее проведенного ранее анализа спектральных характеристик AM сигналов. Для того чтобы получить представление об особенностях спектра колебания с угловой модуляцией, проанализируем его частотный состав для случая однотональной модуляции:
eум(t)= cos [2πfсt+β sin2πFt] (8)
Ширина спектра сигнала при угловой модуляции ограничена той полосой частот, в пределах которой амплитуды спектральных составляющих превосходят некоторое заранее заданное значение.
Рис. 2 Спектр простого колебания с УМ
Часто ширину спектра ЧМ колебания определяют, учитывая все гармоники, величина которых превышает 1 % амплитуды немодулированного несущего. В этом случае количество учитываемых спектральных составляющих k Если модулирующий сигнал не является однотональным, то спектр ЧМ или ФМ колебания оказывается весьма сложным. Однако в частных случаях, когда β <<1 или β >>1 (естественно, с учетом наивысшей модулирующей частоты), ширина спектра определяется такими же соотношениями, как и при тональной модуляции. В реальных системах связи с ЧМ девиация частоты чаше всего значительно превышает ширину спектра модулирующего сигнала, так как именно при этом условии реализуется основное преимущество частотной модуляции — ее большая помехоустойчивость. Это требует по сравнению с амплитудной модуляцией в β раз большей полосы частот канала. Поэтому частотную модуляцию для целей радиосвязи применяют лишь на очень высоких частотах, в диапазонах метровых и более коротких волн. Остановимся кратко на особенностях дискретной модуляции. При дискретной модуляции закодированное сообщение а, представляющее собой последовательность кодовых символов, преобразуется в последовательность элементов (посылок) сигнала u(t). В частном случае дискретная модуляция сводится к воздействию первичного сигнала b(t) на переносчик f(t). Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление тока. Обычно же в качестве переносчика, как и в непрерывной модуляции, используется переменный ток (гармоническое колебание). В этом случае можно получить амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Дискретную модуляцию часто называют манипуляцией, а устройство, осуществляющее дискретную модуляцию (дискретный модулятор), называют манипулятором или генератором сигналов. На рис. 3 приведены формы сигналов при двоичном коде для различных видов манипуляции. При AM символу 1 соответствует передача несущего колебания в течение времени Т (посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания счастотой f1 соответствует символу 1, а передача колебания с частотой f0 соответствует 0. При двоичной ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1.Наконец, на практике нашла применение система относительной фазовой модуляции (ОФМ). В отличие от ФМ, при ОФМ фаза сигналов отсчитывается не от некоторого эталона, а от фазы предыдущего элемента сигнала. В двоичном случае символ 0 передается отрезком синусоиды с начальной фазой предшествующего элемента сигнала, а символ 1 — таким же отрезком с начальной фазой, отличающейся от начальной фазы предшествующего элемента сигнала на 180°. При ОФМ передача начинается с посылки одного, не несущего информации элемента, который служит опорным сигналом для сравнения фазы последующего элемента. В общем случае дискретную модуляцию следует рассматривать как преобразование первичного сигнала b(t) в определенные отрезки сигнала ui(t), где i = 0, 1,..., m —1 — передаваемые символы первичного сигнала. При этом вид отрезка сигнала ui(t), в принципе, может быть произволен. В действительности его выбирают так, чтобы удовлетворить требованиям, предъявляемым к системе связи (в частности, по скорости передачи и по занимаемой полосе частот), и чтобы сигналы хорошо различались с учетом воздействующих помех. Длительность посылки первичного сигнала b(t) при дискретной передаче определяет скорость передачи посылок (техническую скорость или скорость телеграфирования). Эта скорость v выражается числом посылок, передаваемых за единицу времени. Измеряется техническая скорость в Бодах. Один Бод— это скорость, при которой за 1 с передается одна посылка. Если длительность посылки Т выражена в секундах, то скорость манипуляции будет равна v=1/Т, Бод.
Рис.3 Сигналы при разных видах дискретной модуляции
10.Охарактеризуйте существующие методы уплотнения каналов, обоснуйте процесс выбора структуры приемо-передающего тракта и приведите примеры их технической реализации в реальных системах связи.
Ресурс связи представляет время и ширину полосы, доступные для передачи сигнала в определенной системе. Для создания эффективной системы связи необходимо спланировать распределение ресурса между пользователями системы, чтобы время/частота использовались максимально эффективно. Основные способы распределения ресурса связи: 1. Частотное разделение (frequency division— FD). Распределяются определенные под диапазоны используемой полосы частоты. 2. Временное разделение (time division — TD). Пользователям выделяются периодические временные интервалы. В некоторых системах пользователям предоставляется ограниченное время для связи. В других случаях время доступа пользователей к ресурсу определяется динамически. 3. Кодовое разделение (code division — CD). Выделяются определенные элементы набора ортогонально (либо почти ортогонально) распределенных спектральных кодов, каждый из которых использует весь диапазон частот. 4. Пространственное разделение (space division — SD), или многолучевое многократное использование частоты. С помощью точечных лучевых антенн радиосигналы разделяются и направляются в разные стороны. Данный метод допускает многократное использование одного частотного диапазона. 5. Поляризационное разделение (polarization division — PD), или двойное поляризационное многократное использование частоты. Для разделения сигналов применяется ортогональная поляризация, что позволяет использовать один частотный диапазон. Ключевым моментом во всех схемах уплотнения и множественного доступа является то, что при использовании ресурса различными сигналами интерференция не дает неуправляемых взаимных помех, которые делают невозможным процесс детектирования. Интерференция допустима до тех пор, пока сигналы одного канала незначительно увеличивают вероятность появления ошибок в другом канале. Избежать взаимных помех между разными пользователями позволяет использование в разных каналах ортогональных сигналов. Распределение по каналам, характеризующееся ортогональными сигналами, для которых выполняется условие ортогональности во временной области, называют уплотнением с временным разделением (time-division multiplexing — TDM) или множественным доступом с временным разделением (time-division multiple access — TDMA). Распределение по каналам, характеризующееся ортогональными спектрами, для которых выполняется условие ортогональности в частотной области, называют уплотнением с частотным разделением (frequency-division multiplexing — FDM) или множественным доступом с частотным разделением (frequency-division multiple access — FDMA). Используя данные способы распределения ресурсов осуществляют построение многоканальных систем связи. Практика построения современных систем передачи информации показывает, что наиболее дорогостоящими звеньями трактов передачи являются линии связи (кабельные, волоконно-оптические, сотовой мобильной радиосвязи, радиорелейной и спутниковой связи и т. д.). Поскольку экономически нецелесообразно использовать дорогостоящую линию связи для передачи информации единственной паре абонентов, то возникает необходимость построения многоканальных систем передачи, обеспечивающих передачу большого числа сообщений различных источников информации по общей линии связи. Многоканальная передача возможна в тех случаях, когда пропускная способность линии С не меньше суммарной производительности источников информации: С>
Общий принцип построения системы многоканальной передачи поясняется с помощью структурной схемы рисунок 1.
Рисунок 1. Структурная схема многоканальной системы передачи информации
В этой системе первичные сигналы каждого источника b1(t), b2(t),…,bi(t),…,bN(t) с помощью индивидуальных передатчиков (модуляторов) M1, M2,…,Mi,…,MN преобразуются в соответствующие сигналы u1(t), u2(t),…,ui(t),…,uN(t). Совокупность канальных сигналов на выходе устройства объединения ∑ образует групповой сигнал ur(t). В случае раздельной системы уплотнения это объединение сводится к обычному суммированию: иr(t) = Наконец, с учетом частотного диапазона направляющей системы (линии связи) сигнал иr(t) с помощью группового передатчика М преобразуется в линейный сигнал uл(t), который и поступает в линию связи (ЛС). Сначала будем считать, что помеха в канале отсутствует, а канал не вносит искажения в сигнал, т. е. принимаемый линейный сигнал sл(t) = К·uI(t), где К — коэффициент передачи канала, который можно считать равным единице. Тогда на приемном конце линии связи (ЛС) линейный сигнал sл(t) с помощью группового приемника Пр может быть вновь преобразован в групповой сигнал sr(t) = К·uI(t). Канальными, или индивидуальными, приемниками Пр1,Пр2,..,ПрN. из группового сигнала выделяются соответствующие канальные сигналы si(t) = Кui(t), (i = 1,..., N), которые посредством детектирования преобразуются в предназначенные индивидуальным получателям сигналы Канальные передатчики вместе с устройствами объединения образуют аппаратуру объединения (уплотнения) каналов АОК. Групповой передатчик, линия связи ЛС и групповой приемник Пр. составляют групповой тракт передачи, который вместе с аппаратурой объединения и разделения каналов составляет систему многоканальной связи. Индивидуальные приемники Прi системы наряду с выполнением обычной операции преобразования канальных сигналов si(t) в соответствующие первичные сигналы
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.100 (0.016 с.) |

 , 0 < ma< 1 (3)
, 0 < ma< 1 (3) , где fm<<fc, и g(t) не содержит собственной постоянной составляющей. Индекс модуляции та определяет глубину модуляции и часто дается в процентах. На рис. 1 показан характер изменения огибающей при амплитудной модуляции несущей.
, где fm<<fc, и g(t) не содержит собственной постоянной составляющей. Индекс модуляции та определяет глубину модуляции и часто дается в процентах. На рис. 1 показан характер изменения огибающей при амплитудной модуляции несущей.




 = (1/2) Рс
= (1/2) Рс
 ] = cos θ (t)
] = cos θ (t) , около
, около 
 1.
1. 2πfд около 2πfс:
2πfд около 2πfс: 2πf(t)dt = 2πfсt+
2πf(t)dt = 2πfсt+ 

 , а ширина спектра определяется как Fчм=2F·(
, а ширина спектра определяется как Fчм=2F·(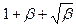 ). Эта формула справедлива для индексов модуляции, заключенных в пределах 0,1
). Эта формула справедлива для индексов модуляции, заключенных в пределах 0,1  24, имеющих наибольший практический интерес.
24, имеющих наибольший практический интерес.
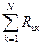 (1)
(1)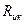 - производительность k-гo источника, а N — число каналов (независимых источников информации). Многоканальные системы, так же как и одноканальные, могут быть аналоговыми и цифровыми. Для унификации аналоговых многоканальных систем за основной или стандартный канал принимают канал тональной частоты, обеспечивающий передачу сообщений с эффективно передаваемой полосой частот 300-3400 Гц, соответствующей основному спектру телефонного сигнала. В цифровых системах передачи наибольшее распространение получили основные цифровые каналы со скоростью 64 Кбит/с. Многоканальные аналоговые системы формируются путем объединения каналов тональной частоты в группы, обычно кратные 12 каналам. Цифровые системы передачи, используемые на сетях связи, формируются в соответствии с принятыми иерархическими структурами.
- производительность k-гo источника, а N — число каналов (независимых источников информации). Многоканальные системы, так же как и одноканальные, могут быть аналоговыми и цифровыми. Для унификации аналоговых многоканальных систем за основной или стандартный канал принимают канал тональной частоты, обеспечивающий передачу сообщений с эффективно передаваемой полосой частот 300-3400 Гц, соответствующей основному спектру телефонного сигнала. В цифровых системах передачи наибольшее распространение получили основные цифровые каналы со скоростью 64 Кбит/с. Многоканальные аналоговые системы формируются путем объединения каналов тональной частоты в группы, обычно кратные 12 каналам. Цифровые системы передачи, используемые на сетях связи, формируются в соответствии с принятыми иерархическими структурами.


 должны обеспечить выделение сигналов si(t) из группового сигнала с допустимыми искажениями. Аппаратуру индивидуальных приемников, обеспечивающую эту операцию, называют аппаратурой разделения каналов (АРК).
должны обеспечить выделение сигналов si(t) из группового сигнала с допустимыми искажениями. Аппаратуру индивидуальных приемников, обеспечивающую эту операцию, называют аппаратурой разделения каналов (АРК).


