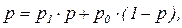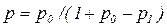Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретный симметричный канал без памятиСодержание книги
Поиск на нашем сайте
Пусть
Р( Дискретный канал называют каналом без памяти, если каждый символ на его выходе зависит только от соответствующего символа на входе, а условная вероятность выходной последовательности
Пусть ошибки любого из символов возникают независимо с вероятностью р, а правильный прием происходит с вероятностью (1-р). Тогда условная вероятность приема символа
Будем далее рассматривать передачу двоичных символов «0» и «1». Вероятность появления n -мерного вектора ошибок, содержащего t единиц, которые соответствуют фактическим ошибкам, равна:
В n -мерном векторе t ошибок могут занимать любые позиции, поэтому несложно определить вероятность появления t ошибок, расположенных как угодно в пределах последовательности длины п:
где Для случая, когда переходная вероятность р << 1, можно найти вероятность ошибочного приема последовательности длины n:
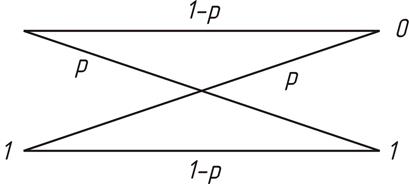
Рассмотренную модель дискретного канала можно изобразить графически в виде переходных вероятностей.
Граф переходных вероятностей двоичного симметричного канала
Данная модель дискретного канала является по сути аналогом рассмотренного выше непрерывного канала с аддитивным «белым» шумом, в котором отсутствуют замирания. Двоичный симметричный канал со стиранием Эта модель является обобщением только что рассмотренной модели в случае, когда на выходе появляется дополнительный третий символ (третье решение), если не удается достоверно опознать переданный элемент сигнала. Для получения такой модели на выходе канала введем двухпороговое устройство с величиной порога
Данный канал называют каналом со стиранием в «нулевой зоне», поскольку здесь может быть правильное решение, если значение порога превышено при фактически переданном символе, ошибочное решение, если превышение порога соответствует непередававшемуся элементу. Наконец, когда амплитуда выходного сигнала Z оказывается в интервале Такой канал можно описать матрицей переходных вероятностей:
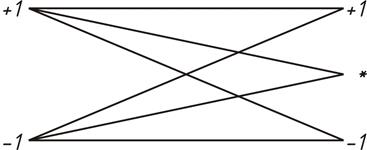
и соответственно графом:
. Граф переходных вероятностей двоичного симметричного канала со стираниями
В отличие от предыдущего здесь произведена замена 0→ +1 и 1 → - 1 Для рассматриваемой модели можно рассчитать вероятность ошибки
и вероятность стирания
где По аналогии с предыдущим можно рассчитать вероятность того, что в последовательности символов длиной n произошло t ошибок и
В заключение отметим, что за счет введения стирания или отказа от принятия решения удается значительно снизить вероятность ошибки, правда за счет возрастания вероятности стирания.
Канал с памятью Канал передачи дискретной информации может быть описан моделью канала с памятью, когда каждый символ выходной последовательности зависит статистически от соответствующего текущего символа, а также от предыдущих входных и выходных вероятностей 1- ро ро р1 1- р1 где: ро — условная вероятность ошибочного приема (к +1)-ого символа, если предыдущий был принят верно; 1- ро - условная вероятность правильного приема (к +1)-ого символа, если предыдущий был принят также верно; р1 - условная вероятность ошибочного приема (к +1)-ого символа при ошибочно принятом предыдущем; 1- р1 - условная вероятность правильного приема (к +1)-ого символа при неверно принятом предыдущем. Средняя (безусловная) вероятность ошибки в этом канале находится из уравнения
отсюда
Данная модель при своей простоте не всегда точно воспроизводит свойства реальных каналов, поэтому разработано достаточно много других более точных, но и более сложных моделей. На них останавливаться не будем, отметим только, что память в канале вызывается различными причинами. Так, одной из них являются замирания в радиоканале. В проводных каналах причиной памяти принято считать коммутационные помехи, возникающие при переключениях, что выводит канал из строя в течение некоторого времени. Иногда причиной памяти могут быть особенности методов модуляции и демодуляции.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.118.36 (0.008 с.) |

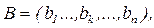 – последовательность символов на входе, а
– последовательность символов на входе, а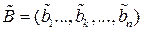 – последовательность символов на выходе канала, к = 1,n.. Тогда вероятность появления символа
– последовательность символов на выходе канала, к = 1,n.. Тогда вероятность появления символа 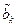 при условии, что bк задано определяют условной или переходной вероятностью
при условии, что bк задано определяют условной или переходной вероятностью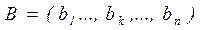 определяется равенством
определяется равенством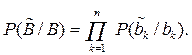
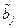 при передаче bi:
при передаче bi: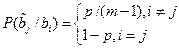
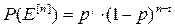
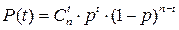
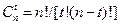 - число различных сочетаний t ошибок (биномиальный коэффициент).
- число различных сочетаний t ошибок (биномиальный коэффициент).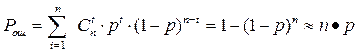
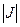 , тогда сигнал, принятый в этом канале, имеет вид:
, тогда сигнал, принятый в этом канале, имеет вид: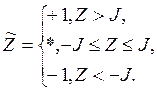
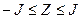 , производится стирание этого символа. Вероятности этих событий равны соответственно
, производится стирание этого символа. Вероятности этих событий равны соответственно 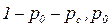 , и pc.
, и pc.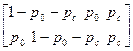
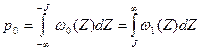
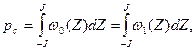
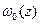 - плотность распределения выходного сигнала канала при передаче символа «0», а
- плотность распределения выходного сигнала канала при передаче символа «0», а 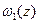 - при передаче «1».
- при передаче «1».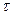 стираний, расположенных на любых местах:
стираний, расположенных на любых местах: