
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость дискретной системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ключевые слова и темы ОБЯЗАТЕЛЬНО прочитайте (не исключено, что списать не дадут) Рекомендуется порядок чтения (для того чтобы получить целостное представление об ОТУ): 1) Передаточные функции ® 2 ) структурные преобразования ® 3) частотные характеристики ® 4) логарифмические характеристики ® 5) звенья САУ ® 6) устойчивость ® 7) характерные частоты САУ ® 8) качество управления ® 9) дискретные САУ ВНИМАНИЕ! В примерах тестов Минобазования – непривычные обозначения: s – оператор Лапласа (в лекциях обозначался p), H(s) или W(s) – передаточная функция (ПФ) (в лекциях обозначалась W(p)) Дискретные системы Модели дискретных систем Порядок модели дискретной системы Z-преобразование Таблица Z-преобразования Передаточная функция дискретной системы Устойчивость дискретной системы Граница устойчивости нейтрального типа дискретной САУ Граница устойчивости колебательного типа дискретной САУ Примеры анализа устойчивости из тестов Минвуза Установившееся значение выхода дискретной САУ при постоянном входном воздействии Установившееся значение ошибки дискретной системы Пример из тестов Минвуза, расчет установившейся ошибки
Звенья САУ. Элементарные звенья и их характеристики. Динамические свойства звеньев и САУ Безынерционное звено Апериодическое звено 1-го порядка Апериодическое звено 2-го порядка Колебательное звено 2-го порядка Консервативное звено Интегрирующее звено(идеальное) Изодромное звено (ПИ-закон управления) Реальное интегрирующее звено (интегрирующее звено с замедлением) Дифференцирующее звено (идеальное) Реальное дифференцирующее звено (дифференцирующее звено с замедлением) Форсирующее звено 1-го порядка Звено запаздывания (чистое запаздывание)
Передаточные функции (ПФ) Относительная степень ПФ Построение ПФ по дифференциальному уравнению САУ Построение частотной ПФ
Структурные преобразования Передаточная функция цепочки последовательно соединенных звеньев Передаточная функция параллельно соединенных звеньев Передаточная функция звена, охваченного обратной связью Узел через звено со входа на выход (по ходу сигнала) Узел через звено с выхода на вход (против хода сигнала) Сумматор через звено со входа на выход (по ходу сигнала) Сумматор через звено с выхода на вход (против хода сигнала) Узел через сумматор (по ходу сигнала) Сумматор через узел (по ходу сигнала)
Устойчивость Необходимое условие устойчивости (Недостаточное) Пример использования необходимого условия По расположению корней на комплексной плоскости Признак устойчивости Признак неустойчивости Признаки границ устойчивости Апериодическая (иначе – нейтральная) граница: нулевой вещественный корень Колебательная граница: чисто мнимые комплексно-сопряженные корни Качество управления Определение Группы показателей качества Классификация по способам определения Прямые показатели (оцениваются непосредственно по графику изменения выхода во времени) Характеризующие свободную составляющую процесса на выходе САУ Время переходного процесса Перерегулирование и наступление 1-го максимума Декремент затухания Частота и период собственных колебаний Число полных колебаний Характеризующие вынужденную составляющую процесса на выходе САУ Статическая ошибка Динамическая ошибка Астатизм, порядок астатизма Коэффициенты ошибок Пример расчета по коэффициентам ошибок из теста: воспроизведение g(t)=20 Косвенные показатели качества управления Показатели, оцениваемые по распределению корней характеристического ур-ния (Время переходного процесса, Колебательность,Затухание) Показатели, оцениваемые по амплитудно-частотной характеристике: (Частота среза, Полоса пропускания, Резонансная частота, Колебательность, Время переходного процесса, Момент наступления первого максимума) Показатели, оцениваемые по логарифмической АЧХ
Характерные частоты САУ Частота среза Частота, соответствующая полосе пропускания Резонансная частота
Частотные характеристики Определение и построение амплитудно-частотная (АЧХ) фазовая частотная (ФЧХ) Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ). Построение ЛАЧХ, пример Характерные частоты, определяемые по ЛАЧХ Частота среза на ЛАЧХ Примеры расчета с ЛАЧХ из теста МиНОБРАЗОВАНИЯ (см. также ЛАЧХ и ЛФЧХ в разделе «Звенья САУ») Разъяснения терминов и тем Дискретные системы Модели дискретных линейных систем класса «скалярный вход u [ n ] – скалярный выход y [ n ]» задаются обычно в форме разностных уравнений, связывающих значение выхода объекта на некотором такте со значениями выхода объекта в предшествующих тактах (инерционность) и входа в этом же такте и нескольких предшествующих тактах. Продолжительность такта T – постоянна, такт с номером n соответствует моменту времени (nT). В промежутках между тактами значения входа и выхода не рассматриваются. Пример 1 модели в общем виде (определение текущего значения выхода по предыстории). В примере видно, что значение выхода y [ n ] зависит от предшествующих значений выхода в тактах [ n– 1], [ n– 2],…, [ n–M ] и от управляющих воздействий в тактах [ n– 1], [ n– 2],…, [ n–R ]. Параметрами модели являются коэффициенты ai, i =1,…, M и bk, k = 1,.., R. Обычно R<M, гораздо реже R=M, почти никогда R>M Порядок модели дискретной системы определяется значением M. Модель 1-го порядка: Модель 2-го порядка: Пример 2 модели в общем виде (расчет будущего значения выхода по текущему значению)
Модель 1-го порядка: Модель 2-го порядка: Пример из теста Минвуза: определить порядок разностного уравнения
Z-преобразование Используется для получения передаточных функций дискретных систем (форма ПФ аналогична ПФ непрерывных систем). Z-преобразование = дискретному варианту преобразования Лапласа, используемому в непрерывных системах: вместо Таблица Z-преобразования ставит в соответствие некоторые оригиналы и изображения (не для всех изображений удается найти оригиналы).
Передаточная функция дискретной системы есть отношение z-изображения выхода к z-изображению входа. Строится по модели дискретной системы. Например, для модели вида 2, т.е.
Качество управления Определение: показатели качества управления – это субъективные характеристики процессов в САУ, зависящие от требований Заказчика и от опыта проектировщика САУ (в отличие от объективных характеристик – например, устойчивости). Группы показателей качества – характеризующие: 1) точность; 2) быстродействие; 3) степень устойчивости; 4) комплексно – все три вида показателей. Способы определения: 1) – непосредственно по обработке данных о реакциях САУ на типовые воздействия (прямые показатели качества); 2) по косвенным данным (по частотным характеристикам, расположению корней <знаменатель ПФ=0>; по корневым годографам…)
Прямые показатели (оцениваются непосредственно по графику изменения выхода во времени) На рис. – типичный переходный процесс отработки ненулевых начальных условий при внешних воздействиях = 0.
А) Показатели, характеризующие свободную составляющую процесса на выходе САУ 1) Время переходного процесса
2) Перерегулирование и наступление 1-го максимума
3) Декремент затухания
4) Частота и период собственных колебаний
5) Число полных колебаний
Б) Показатели, характеризующие вынужденную составляющую процесса на выходе САУ 1) Статическая ошибка
2 ) Динамическая ошибка
3) Астатизм, порядок астатизма Определение: САУ, замкнутая обратной связью, обладает астатизмом k- го порядка, если в прямой цепи соответствующей ей разомкнутой САУ содержится сомножитель pk (иными словами, в структуре разомкнутой САУ имеется цепь из k интегрирующих звеньев, включенных последовательно). Частные случаи: а) при астатизме 1-го порядка постоянные задающие воздействия воспроизводятся без ошибки (отсутствует статическая ошибка). При переменных задающих воздействиях имеется ненулевая динамическая ошибка. б) При астатизме 2-го порядка постоянные и линейно зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых отличается от линейной, имеется ненулевая динамическая ошибка. в). При астатизме 3-го порядка постоянные, линейно и квадратично зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых более сложна, чем квадратичная, имеется динамическая ошибка.
Здесь С 0, С 1,…, Сm – коэффициенты ошибок, вычисляются по передаточной функции (ПФ) по каналу «задающее воздействие g (t) – рассогласование e (t) между задающим воздействием и выходом САУ» и по производным этой ПФ при s =0 (это соответствует t ®¥):
ПФ по каналу «задающее воздействие g (t) – рассогласование e (t)» вычисляется по формуле:
Здесь W пр(s), WОС (s) – соответственно ПФ прямой цепи и цепи обратной связи.
Вычисления проиллюстрируем примером. Пусть задающее воздействие линейно зависит от времени:
Требуется найти установившееся значение ошибки e уст(t) при этом задающем воздействии. Задана передаточная функция разомкнутой САУ (ПФ прямой цепи), она равна Шаг 1. Рассчитываем передаточную функцию САУ по каналу «задающее воздействие – рассогласование».
Соответствующая ПФ равна:
В примере W ОС(s) =1, Шаг 2. Рассчитываем коэффициенты ошибок. Для рассматриваемого примера нужна только первая производная ПФ Wge(s) при s=0: старшие производные не потребуются, т.к. все производные задающего воздействия в примере выше первой равны нулю. После вычисления полагаем s = 0. Получим коэффициенты ошибок:
Шаг 3. Рассчитываем первую производную задающего воздействия:
Шаг 4. Пользуясь формулой с коэффициентами ошибок, находим: установившееся значение рассогласования e (t) между задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом равно:
Косвенные показатели качества А) Показатели, оцениваемые по распределению корней характеристического уравнения <знаменатель передаточной функции замкнутой САУ = 0>: Время переходного процесса, Колебательность, Затухание – см. рис. ниже
Б) Показатели, оцениваемые по амплитудно-частотной характеристике замкнутой САУ: Частота среза, Полоса пропускания, Резонансная частота, Колебательность, Время переходного процесса, Момент времени наступления первого максимума – см. рисунок ниже
В) Показатели, оцениваемые по логарифмической амплитудно-частотной характеристике разомкнутой САУ: частота среза; время переходного процесса; момент времени, при котором наступает перерегулирование.
Примеры с ЛАЧХ, включенные в тест Минобразования: 1)Среднечастотная часть логарифмической амплитудно-частотной характеристики определяет… (из формулы, показанной на рисунке выше, ясен ответ: время переходного процесса и перерегулирование) 2)
Передаточные функции (ПФ)
Относительной степенью передаточной функции называется РАЗНОСТЬ СТЕПЕНЕЙ ЗНАМЕНАТЕЛЯ И ЧИСЛИТЕЛЯ передаточной функции Построение передаточной функции по дифференциальному уравнению, пример. Задание: построить ПФ по уравнению Решение: ПФ имеет форму дроби (в лекциях обозначали W, в тестах обозначена H), используется оператор Лапласа (в лекциях обозначали p, в тестах обозначение s). По определению ПФ есть отношение изображения (по Лапласу) выхода объекта к изображению входа. Построение ПФ: в числителе – многочлен s правой части уравнения, степени элементов многочлена соответствуют порядку производной. В примере числитель: s + 5. В знаменателе – аналогичный многочлен левой части. В примере: s2 + 2. ВНИМАНИЕ: не записывайте s0 при элементах уравнения, не являющихся производными. Ответ в примере: Устойчивость Необходимое (но недостаточное) условие устойчивости: все знаки при элементах знаменателя ПФ ОДИНАКОВЫ. Пример: пусть ПФ разомкнутой САУ равна Звено чистого запаздывания Уравнение Передаточная функция (ПФ) Частотная ПФ Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой Фазовая частотная характеристика Логарифмическая амплитудная характеристика: равна 20×lg(K), проходит параллельно абсциссе; Характерный параметр – наклон (0). Логарифмическая фазовая частотная характеристика Ключевые слова и темы ОБЯЗАТЕЛЬНО прочитайте (не исключено, что списать не дадут) Рекомендуется порядок чтения (для того чтобы получить целостное представление об ОТУ): 1) Передаточные функции ® 2 ) структурные преобразования ® 3) частотные характеристики ® 4) логарифмические характеристики ® 5) звенья САУ ® 6) устойчивость ® 7) характерные частоты САУ ® 8) качество управления ® 9) дискретные САУ ВНИМАНИЕ! В примерах тестов Минобазования – непривычные обозначения: s – оператор Лапласа (в лекциях обозначался p), H(s) или W(s) – передаточная функция (ПФ) (в лекциях обозначалась W(p)) Дискретные системы Модели дискретных систем Порядок модели дискретной системы Z-преобразование Таблица Z-преобразования Передаточная функция дискретной системы Устойчивость дискретной системы Граница устойчивости нейтрального типа дискретной САУ Граница устойчивости колебательного типа дискретной САУ Примеры анализа устойчивости из тестов Минвуза Установившееся значение выхода дискретной САУ при постоянном входном воздействии Установившееся значение ошибки дискретной системы Пример из тестов Минвуза, расчет установившейся ошибки
Звенья САУ. Элементарные звенья и их характеристики. Динамические свойства звеньев и САУ Безынерционное звено Апериодическое звено 1-го порядка Апериодическое звено 2-го порядка Колебательное звено 2-го порядка Консервативное звено Интегрирующее звено(идеальное) Изодромное звено (ПИ-закон управления) Реальное интегрирующее звено (интегрирующее звено с замедлением) Дифференцирующее звено (идеальное) Реальное дифференцирующее звено (дифференцирующее звено с замедлением) Форсирующее звено 1-го порядка Звено запаздывания (чистое запаздывание)
Передаточные функции (ПФ) Относительная степень ПФ Построение ПФ по дифференциальному уравнению САУ Построение частотной ПФ
Структурные преобразования Передаточная функция цепочки последовательно соединенных звеньев Передаточная функция параллельно соединенных звеньев Передаточная функция звена, охваченного обратной связью Узел через звено со входа на выход (по ходу сигнала) Узел через звено с выхода на вход (против хода сигнала) Сумматор через звено со входа на выход (по ходу сигнала) Сумматор через звено с выхода на вход (против хода сигнала) Узел через сумматор (по ходу сигнала) Сумматор через узел (по ходу сигнала)
Устойчивость Необходимое условие устойчивости (Недостаточное) Пример использования необходимого условия По расположению корней на комплексной плоскости Признак устойчивости Признак неустойчивости Признаки границ устойчивости Апериодическая (иначе – нейтральная) граница: нулевой вещественный корень Колебательная граница: чисто мнимые комплексно-сопряженные корни Качество управления Определение Группы показателей качества Классификация по способам определения Прямые показатели (оцениваются непосредственно по графику изменения выхода во времени) Характеризующие свободную составляющую процесса на выходе САУ Время переходного процесса Перерегулирование и наступление 1-го максимума Декремент затухания Частота и период собственных колебаний Число полных колебаний Характеризующие вынужденную составляющую процесса на выходе САУ Статическая ошибка Динамическая ошибка Астатизм, порядок астатизма Коэффициенты ошибок Пример расчета по коэффициентам ошибок из теста: воспроизведение g(t)=20 Косвенные показатели качества управления Показатели, оцениваемые по распределению корней характеристического ур-ния (Время переходного процесса, Колебательность,Затухание) Показатели, оцениваемые по амплитудно-частотной характеристике: (Частота среза, Полоса пропускания, Резонансная частота, Колебательность, Время переходного процесса, Момент наступления первого максимума) Показатели, оцениваемые по логарифмической АЧХ
Характерные частоты САУ Частота среза Частота, соответствующая полосе пропускания Резонансная частота
Частотные характеристики Определение и построение амплитудно-частотная (АЧХ) фазовая частотная (ФЧХ) Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ). Построение ЛАЧХ, пример Характерные частоты, определяемые по ЛАЧХ Частота среза на ЛАЧХ Примеры расчета с ЛАЧХ из теста МиНОБРАЗОВАНИЯ (см. также ЛАЧХ и ЛФЧХ в разделе «Звенья САУ») Разъяснения терминов и тем Дискретные системы Модели дискретных линейных систем класса «скалярный вход u [ n ] – скалярный выход y [ n ]» задаются обычно в форме разностных уравнений, связывающих значение выхода объекта на некотором такте со значениями выхода объекта в предшествующих тактах (инерционность) и входа в этом же такте и нескольких предшествующих тактах. Продолжительность такта T – постоянна, такт с номером n соответствует моменту времени (nT). В промежутках между тактами значения входа и выхода не рассматриваются. Пример 1 модели в общем виде (определение текущего значения выхода по предыстории). В примере видно, что значение выхода y [ n ] зависит от предшествующих значений выхода в тактах [ n– 1], [ n– 2],…, [ n–M ] и от управляющих воздействий в тактах [ n– 1], [ n– 2],…, [ n–R ]. Параметрами модели являются коэффициенты ai, i =1,…, M и bk, k = 1,.., R. Обычно R<M, гораздо реже R=M, почти никогда R>M Порядок модели дискретной системы определяется значением M. Модель 1-го порядка: Модель 2-го порядка: Пример 2 модели в общем виде (расчет будущего значения выхода по текущему значению)
Модель 1-го порядка: Модель 2-го порядка: Пример из теста Минвуза: определить порядок разностного уравнения
Z-преобразование Используется для получения передаточных функций дискретных систем (форма ПФ аналогична ПФ непрерывных систем). Z-преобразование = дискретному варианту преобразования Лапласа, используемому в непрерывных системах: вместо Таблица Z-преобразования ставит в соответствие некоторые оригиналы и изображения (не для всех изображений удается найти оригиналы).
Передаточная функция дискретной системы есть отношение z-изображения выхода к z-изображению входа. Строится по модели дискретной системы. Например, для модели вида 2, т.е.
Устойчивость дискретной системы Шаг 1. Нужно записать уравнение дискретной САУ в форме
Граница устойчивости нейтрального типа имеет место, если все корни характеристического уравнения – внутри единичного круга, кроме единственного, находящегося на действительной оси комплексной плоскости в точке пересечения с окружностью единичного радиуса. В системе, находящейся на границе устойчивости нейтрального типа, выход объекта после снятия внешнего воздействия не возвращается в нуль, но и не уходит в бесконечность.
Граница устойчивости колебательного типа имеет место, если все корни характеристического уравнения – внутри единичного круга, кроме пары корней, лежащих на окружности единичного радиуса (не в точке пересечения с действительной осью). В системе, находящейся на границе устойчивости колебательного типа, выход объекта после снятия внешнего воздействия периодически изменяет знак дискретного сигнала (аналог незатухающих колебаний в непрерывных системах).
К примерам из тестов Минвуза об устойчивости дискретных систем
Пример: уравнение динамики САУ Пример из тестов Минвуза: В замкнутой системе, описываемой разностным уравнением Установившееся значение выхода дискретной САУ при постоянном входном воздействии. Задача имеет смысл только для устойчивой системы. Для расчета нужно положить
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.209 (0.016 с.) |




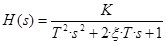


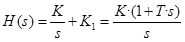




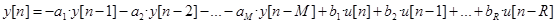 .
.

 Порядок модели дискретной системы определяется значением M.
Порядок модели дискретной системы определяется значением M.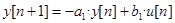

 , где T – период квантования, n = 0,1,… – дискретное время (такты). Ответ: порядок равен 2.
, где T – период квантования, n = 0,1,… – дискретное время (такты). Ответ: порядок равен 2.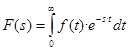 (преобразование непрерывной функции времени f(t) в изображение F(s), s – оператор Лапласа) в дискретных системах используется сумма, заменяющая интеграл:
(преобразование непрерывной функции времени f(t) в изображение F(s), s – оператор Лапласа) в дискретных системах используется сумма, заменяющая интеграл: 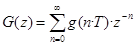 (получено так: при замене интеграла суммой получилось
(получено так: при замене интеграла суммой получилось  , потом обозначили
, потом обозначили 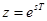 ). Здесь g (nT) – оригинал, G (z) – изображение.
). Здесь g (nT) – оригинал, G (z) – изображение.
 (степени z трактуются как задержки на соответствующее число тактов по сравнению с y [ n + M ])
(степени z трактуются как задержки на соответствующее число тактов по сравнению с y [ n + M ])







 4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула:
4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула:


 .
.
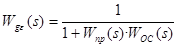
 ,
,  .
. (это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует).
(это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует). 

 Это и будет решением данного примера.
Это и будет решением данного примера.


 …
… . Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.
. Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.
 , происходит замыкание единичной положительной обратной связи. Получим:
, происходит замыкание единичной положительной обратной связи. Получим:  ’ Слагаемые в знаменателе имеют РАЗНЫЕ знаки, САУ неустойчива.
’ Слагаемые в знаменателе имеют РАЗНЫЕ знаки, САУ неустойчива. , где y (t), u (t) – соответственно выход и вход звена; K, t – соответственно коэффициент усиления и время запаздывания.
, где y (t), u (t) – соответственно выход и вход звена; K, t – соответственно коэффициент усиления и время запаздывания.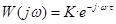
 (постоянна при всех частотах w ).
(постоянна при всех частотах w ). .
. (можно принять внешнее воздействие = 0, т.к. факт устойчивости – внутреннее свойство системы, от внешнего воздействия не зависит). Шаг 2. Найти корни характеристического уравнения
(можно принять внешнее воздействие = 0, т.к. факт устойчивости – внутреннее свойство системы, от внешнего воздействия не зависит). Шаг 2. Найти корни характеристического уравнения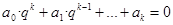 (корни могут быть действительными и/или попарно комплексно-сопряженными, общее число корней k). Шаг 3. Установить факт устойчивости по теореме: в устойчивой дискретной САУ все корни должны лежать внутри круга единичного радиуса на комплексной плоскости: т.е. для всех qi, i = 1,…, k
(корни могут быть действительными и/или попарно комплексно-сопряженными, общее число корней k). Шаг 3. Установить факт устойчивости по теореме: в устойчивой дискретной САУ все корни должны лежать внутри круга единичного радиуса на комплексной плоскости: т.е. для всех qi, i = 1,…, k  . Здесь Re(…), Im(…) – соответственно действительная и мнимая часть корня. Если хотя бы для одного корня
. Здесь Re(…), Im(…) – соответственно действительная и мнимая часть корня. Если хотя бы для одного корня  , САУ неустойчива. ВНИМАНИЕ: в отличие от систем с непрерывным временем анализ устойчивости НЕ ориентируется на знак вещественной части корней!
, САУ неустойчива. ВНИМАНИЕ: в отличие от систем с непрерывным временем анализ устойчивости НЕ ориентируется на знак вещественной части корней!

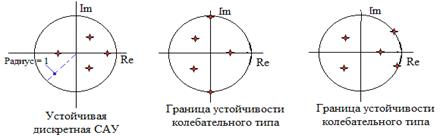

 , в нем внешнее воздействие (=10) при анализе устойчивости не учитывается. Характеристическое уравнение:
, в нем внешнее воздействие (=10) при анализе устойчивости не учитывается. Характеристическое уравнение:  . Корни
. Корни  система устойчива.
система устойчива. , где Т – период квантования, n= 0,1,… – дискретное время, g(…) –входная переменная, y(…) – выходная переменная, найти корень характеристического уравнения. Решение: корень находится из уравнения q – 0.2 = 0, т.е. q = 0.2.
, где Т – период квантования, n= 0,1,… – дискретное время, g(…) –входная переменная, y(…) – выходная переменная, найти корень характеристического уравнения. Решение: корень находится из уравнения q – 0.2 = 0, т.е. q = 0.2. и решить соответствующее алгебраическое уравнение относительно установившегося значение выхода y уст. Пример: уравнение динамики САУ
и решить соответствующее алгебраическое уравнение относительно установившегося значение выхода y уст. Пример: уравнение динамики САУ  , получим
, получим 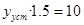 , отсюда
, отсюда 



