
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Установившееся значение ошибки дискретной системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определяется, если задано уравнение динамики системы и закон изменения задающего воздействия g [ n ] при значениях тактов n >n*, начиная с n*, после которого можно считать, что действие начальных условий «забыто» (т.е. их влиянием можно пренебречь). Возможно, закон изменения задающего воздействия задан в форме z-преобразования G0(z). Тогда для определения g [ n ] нужно использовать таблицу обратного преобразования из G0(z) в g [ n ].. Пример из тестов Минвуза: Пусть динамика разомкнутого контура системы описывается разностным уравнением Решение: ошибка на n- мтакте работы САУ с отрицательной обратной связью равна разности между задающим воздействием и выходом САУ, т.е. Уравнение ошибки найдем, вычитая выход из задания:
Качество управления Определение: показатели качества управления – это субъективные характеристики процессов в САУ, зависящие от требований Заказчика и от опыта проектировщика САУ (в отличие от объективных характеристик – например, устойчивости). Группы показателей качества – характеризующие: 1) точность; 2) быстродействие; 3) степень устойчивости; 4) комплексно – все три вида показателей. Способы определения: 1) – непосредственно по обработке данных о реакциях САУ на типовые воздействия (прямые показатели качества); 2) по косвенным данным (по частотным характеристикам, расположению корней <знаменатель ПФ=0>; по корневым годографам…)
Прямые показатели (оцениваются непосредственно по графику изменения выхода во времени) На рис. – типичный переходный процесс отработки ненулевых начальных условий при внешних воздействиях = 0.
А) Показатели, характеризующие свободную составляющую процесса на выходе САУ 1) Время переходного процесса
2) Перерегулирование и наступление 1-го максимума
3) Декремент затухания
4) Частота и период собственных колебаний
5) Число полных колебаний
Б) Показатели, характеризующие вынужденную составляющую процесса на выходе САУ
1) Статическая ошибка
2 ) Динамическая ошибка
3) Астатизм, порядок астатизма Определение: САУ, замкнутая обратной связью, обладает астатизмом k- го порядка, если в прямой цепи соответствующей ей разомкнутой САУ содержится сомножитель pk (иными словами, в структуре разомкнутой САУ имеется цепь из k интегрирующих звеньев, включенных последовательно). Частные случаи: а) при астатизме 1-го порядка постоянные задающие воздействия воспроизводятся без ошибки (отсутствует статическая ошибка). При переменных задающих воздействиях имеется ненулевая динамическая ошибка. б) При астатизме 2-го порядка постоянные и линейно зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых отличается от линейной, имеется ненулевая динамическая ошибка. в). При астатизме 3-го порядка постоянные, линейно и квадратично зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых более сложна, чем квадратичная, имеется динамическая ошибка.
Здесь С 0, С 1,…, Сm – коэффициенты ошибок, вычисляются по передаточной функции (ПФ) по каналу «задающее воздействие g (t) – рассогласование e (t) между задающим воздействием и выходом САУ» и по производным этой ПФ при s =0 (это соответствует t ®¥):
ПФ по каналу «задающее воздействие g (t) – рассогласование e (t)» вычисляется по формуле:
Здесь W пр(s), WОС (s) – соответственно ПФ прямой цепи и цепи обратной связи.
Вычисления проиллюстрируем примером. Пусть задающее воздействие линейно зависит от времени:
Требуется найти установившееся значение ошибки e уст(t) при этом задающем воздействии. Задана передаточная функция разомкнутой САУ (ПФ прямой цепи), она равна Шаг 1. Рассчитываем передаточную функцию САУ по каналу «задающее воздействие – рассогласование».
Соответствующая ПФ равна:
В примере W ОС(s) =1, Шаг 2. Рассчитываем коэффициенты ошибок. Для рассматриваемого примера нужна только первая производная ПФ Wge(s) при s=0: старшие производные не потребуются, т.к. все производные задающего воздействия в примере выше первой равны нулю. После вычисления полагаем s = 0. Получим коэффициенты ошибок:
Шаг 3. Рассчитываем первую производную задающего воздействия:
Шаг 4. Пользуясь формулой с коэффициентами ошибок, находим: установившееся значение рассогласования e (t) между задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом равно:
Косвенные показатели качества А) Показатели, оцениваемые по распределению корней характеристического уравнения <знаменатель передаточной функции замкнутой САУ = 0>: Время переходного процесса, Колебательность, Затухание – см. рис. ниже
Б) Показатели, оцениваемые по амплитудно-частотной характеристике замкнутой САУ: Частота среза, Полоса пропускания, Резонансная частота, Колебательность, Время переходного процесса, Момент времени наступления первого максимума – см. рисунок ниже
В) Показатели, оцениваемые по логарифмической амплитудно-частотной характеристике разомкнутой САУ: частота среза; время переходного процесса; момент времени, при котором наступает перерегулирование.
Примеры с ЛАЧХ, включенные в тест Минобразования: 1)Среднечастотная часть логарифмической амплитудно-частотной характеристики определяет… (из формулы, показанной на рисунке выше, ясен ответ: время переходного процесса и перерегулирование) 2)
Передаточные функции (ПФ)
Относительной степенью передаточной функции называется РАЗНОСТЬ СТЕПЕНЕЙ ЗНАМЕНАТЕЛЯ И ЧИСЛИТЕЛЯ передаточной функции Построение передаточной функции по дифференциальному уравнению, пример. Задание: построить ПФ по уравнению Решение: ПФ имеет форму дроби (в лекциях обозначали W, в тестах обозначена H), используется оператор Лапласа (в лекциях обозначали p, в тестах обозначение s). По определению ПФ есть отношение изображения (по Лапласу) выхода объекта к изображению входа. Построение ПФ: в числителе – многочлен s правой части уравнения, степени элементов многочлена соответствуют порядку производной. В примере числитель: s + 5. В знаменателе – аналогичный многочлен левой части. В примере: s2 + 2. ВНИМАНИЕ: не записывайте s0 при элементах уравнения, не являющихся производными. Ответ в примере:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.194.15 (0.011 с.) |

 . На вход системы, замкнутой обратной связью, подано возрастающее входное воздействие 2 n. Учитывая, что Z-преобразование такого сигнала равно
. На вход системы, замкнутой обратной связью, подано возрастающее входное воздействие 2 n. Учитывая, что Z-преобразование такого сигнала равно  , найти установившееся значение ошибки.
, найти установившееся значение ошибки. . В этом примере Z-преобразование только затуманивает результат. Расчет: в установившемся режиме
. В этом примере Z-преобразование только затуманивает результат. Расчет: в установившемся режиме 









 4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула:
4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула:


 .
.
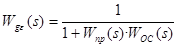
 ,
,  .
. (это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует).
(это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует). 

 Это и будет решением данного примера.
Это и будет решением данного примера.


 …
… . Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.
. Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.



