
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соответствующие разным вероятностям допустимой ошибкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И разным степеням свободы
экспериментально подтвердилась: успеваемость значительно улучшилась, и это мы можем утверждать, допуская ошибку, не превышающую 0,001%. Иногда в психолого-педагогическом эксперименте возникает необходимость сравнить дисперсии двух выборок для того, чтобы решить, различаются ли эти дисперсии между собой. Допустим, что проводится эксперимент, в котором проверяется гипотеза о том, что одна из двух предлагаемых программ или методик обучения обеспечивает одинаково успешное усвоение знаний учащимися с разными способностями, а другая программа или методика этим свойством не обладает. Демонстрацией справедливости такой гипотезы было бы доказательство того, что индивидуальный разброс оценок учащихся по одной программе или методике больше (или меньше), чем индивидуальный разброс оценок по другой программе или методике. Критерий Фишера Подобного рода задачи решаются, в частности, при помощи критерия Фишера. Его формула выглядит следующим образом:
где n1 — количество значения признака в первой из сравниваемых выборок; п2 — количество значений признака во второй из сравниваемых выборок; (п 1 — 1, п2 — 1) — число степеней свободы;
Вычисленное с помощью этой формулы значение F-критерия сравнивается с табличным (табл. 34), и если оно превосходит табличное для избранной вероятности допустимой ошибки и заданного числа степеней свободы, то делается вывод о том, что гипотеза о различиях в дисперсиях подтверждается. В противоположном случае такая гипотеза отвергается и дисперсии считаются одинаковыми1. Таблица 34 Граничные значения F-критерия для вероятности допустимой ошибки 0,05 и числа степеней свободы n1и n2
1. Если отношение выборочных дисперсий в формуле F-критерия оказывается меньше единицы, то числитель и знаменатель в этой формуле меняют местами и вновь определяют значения критерия. Примечание. Таблица для граничных значений F-распределения приведена в сокращенном виде. Полностью ее можно найти в справочниках по математической статистике, в частности в тех, которые даны в списке дополнительной литературы представленной в Теме № 1.. Пример. Сравним дисперсии следующих двух рядов цифр с целью определения статистически достоверных различий между ними. Первый ряд: 4,6,5,7,3,4,5,6. Второй ряд: 2,7,3,6,1,8,4,5. Средние значения для двух этих рядов соответственно равны: 5,0 и 4,5. Их дисперсии составляют: 1,5 и 5,25. Частное от деления большей дисперсии на меньшую равно 3,5. Это и есть искомый показатель F. Сравнивая его с табличным граничным значением 3,44, приходим к выводу о том, что дисперсии двух сопоставляемых выборок действительно отличаются друг от друга на уровне значимости более 95% или с вероятностью допустимой ошибки не более 0,05%.
МЕТОД КОРЕЛЛЯЦИЙ
Следующий метод вторичной статистической обработки, посредством которого выясняется связь или прямая зависимость между двумя рядами экспериментальных данных, носит название метод корреляций. Он показывает, каким образом одно явление влияет на другое или связано с ним в своей динамике. Подобного рода зависимости существуют, к примеру, между величинами, находящимися в причинно-следственных связях друг с другом. Если выясняется, что два явления статистически достоверно коррелируют друг с другом и если при этом есть уверенность в том, что одно из них может выступать в качестве причины другого явления, то отсюда определенно следует вывод о наличии между ними причинно-следственной зависимости.
Имеется несколько разновидностей данного метода: *линейный, *ранговый, *парный и *множественный. Линейный корреляционный анализ позволяет устанавливать прямые связи между переменными величинами по их абсолютным значениям. Эти связи графически выражаются прямой линией, отсюда название «линейный». Ранговая корреляция определяет зависимость не между абсолютными значениями переменных, а между порядковыми местами, или рангами, занимаемыми ими в упорядоченном по величине ряду. Парный корреляционный анализ включает изучение корреляционных зависимостей только между парами переменных, а множественный, или многомерный, — между многими переменными одновременно. Распространенной в прикладной статистике формой многомерного корреляционного анализа является факторный анализ. На рис. 74 в виде множества точек представлены различные виды зависимостей между двумя переменными X и У (различные поля корреляций между ними). На фрагменте рис. 74, отмеченном буквой А, точки случайным образом разбросаны по координатной плоскости. Здесь по величине X нельзя делать какие-либо определенные выводы о величине Y. Если в данном случае подсчитать коэффициент корреляции, то он будет равен 0, что свидетельствует о том, что достоверная связь между X и У отсутствует (она может отсутствовать и тогда, когда коэффициент корреляции не равен 0, но близок к нему по величине). На фрагменте Б рисунка все точки лежат на одной прямой, и каждому отдельному значению переменной X можно поставить в соответствие одно и только одно значение переменной У, причем, чем больше X, тем больше У. Такая связь между переменными X и У называется прямой, и если это прямая, соответствующая уравнению регрессии, то связанный с ней коэффициент корреляции будет равен +1. (Заметим, что в жизни такие случаи практически не встречаются; коэффициент корреляции почти никогда не достигает величины единицы.) На фрагменте В рисунка коэффициент корреляции также будет равен единице, но с отрицательным знаком: -1. Это означает обратную зависимость между переменными X и У, т.е., чем больше одна из них, тем меньше другая. На фрагменте Г рисунка точки также разбросаны не случайно, они имеют тенденцию группироваться в определенном направлении. Это направление приближенно может быть представлено уравнением прямой регрессии. Такая же особенность, но с противоположным знаком, характерна для фрагмента Д. Соответствующие этим двум фрагментам коэффициенты корреляции приблизительно будут равны +0,50 и -0,30. Заметим, что крутизна графика, или линии регрессии, не оказывает влияния на величину коэффициента корреляции.
Рис. 74. Схематическое представление различных корреляционных зависимостей с соответствующими значениями коэффициента линейной корреляции (цит. по: Иберла К. Факторный анализ. М,, 1980).
Наконец, фрагмент Е дает коэффициент корреляции, равный или близкий к 0, так как в данном случае связь между переменными хотя и существует, но не является линейной. Коэффициент линейной корреляции определяется при помощи следующей формулы:
где rxy — коэффициент линейной корреляции; х, у - средние выборочные значения сравниваемых величин; хi,уi — частные выборочные значения сравниваемых величин; п — общее число величин в сравниваемых рядах показателей;
средних значений. Пример. Определим коэффициент линейной корреляции между следующими двумя рядами показателей. Ряд 1: 2, 4, 4, 5, 3, б, 8. Ряд II: 2, 5, 4, 6, 2, 5, 7. Средние значения этих двух рядов соответственно равны 4,6 и 4,4. Их дисперсии составляют следующие величины: 3,4 и 3,1. Подставив эти данные в приведенную выше формулу коэффициента линейной корреляции, получим следующий результат: 0,92. Следовательно, между рядами данных существует значимая связь, причем довольно явно выраженная, так как коэффициент корреляции близок к единице. Действительно, взглянув на эти ряды цифр, мы обнаруживаем, что большей цифре в одном ряду соответствует большая цифра в другом ряду и, наоборот, меньшей цифре в одном ряду соответствует примерно такая же малая цифра в другом ряду. К коэффициенту ранговой корреляции в психолого-педагогических исследованиях обращаются в том случае, когда признаки, между которыми устанавливается зависимость, являются качественно различными и не могут быть достаточно точно оценены при помощи так называемой интервальной измерительной шкалы. Интервальной называют такую шкалу, которая позволяет оценивать расстояния между ее значениями и судить о том, какое из них больше и насколько больше другого. Например, линейка, с помощью которой оцениваются и сравниваются длины объектов, является интервальной шкалой, так как, пользуясь ею, мы можем утверждать, что расстояние между двумя и шестью сантиметрами в два раза больше, чем расстояние между шестью и восемью сантиметрами. Если же, пользуясь некоторым измерительным инструментом, мы можем только утверждать, что одни показатели больше других, но не в состоянии сказать на сколько, то такой измерительный инструмент называется не интервальным, а порядковым. Большинство показателей, которые получают в психолого-педагогических исследованиях, относятся к порядковым, а не к интервальным шкалам (например, оценки типа «да», «нет», «скорее нет, чем да» и другие, которые можно переводить в баллы), поэтому коэффициент линейной корреляции к ним неприменим. В этом случае обращаются к использованию коэффициента ранговой корреляции, формула которого следующая:
где Rs — коэффициент ранговой корреляции по Спирмену; di — разница между рангами показателей одних и тех же испытуемых в упорядоченных рядах; п — число испытуемых или цифровых данных (рангов) в коррелируемых рядах. Пример. Допустим, что экспериментатора интересует, влияет ли интерес учащихся к учебному предмету на их успеваемость. Предположим, что с помощью некоторой психодиагностической методики удалось измерить величину интереса к учению и выразить его для десяти учащихся в следующих цифрах: 5, 6, 7, 8, 2, 4, 8, 7, 2, 9. Допустим также, что при помощи другой методики были определены средние оценки этих же учащихся по данному предмету, оказавшиеся соответственно равными: 3,2; 4,0; 4,1; 4,2; 2,5; 5,0; 3,0; 4,8; 4,6; 2,4. Упорядочим оба ряда оценок по величине цифр и припишем каждому из учащихся по два ранга; один из них указывает на то, какое место среди остальных данных ученик занимает по успеваемости, а другой — на то, какое место среди них же он занимает по интересу к учебному предмету. Ниже приведены ряды цифр, два из которых (первый и третий) представляют исходные данные, а два других (второй и четвертый) — соответствующие ранги1:
Определив сумму квадратов различий в рангах (∑d2i) и подставив нужное значение в числитель формулы, получаем, что коэффициент ранговой корреляции равен 0,97, т.е. достаточно высок, что и говорит о том, что между интересом к учебному предмету и успеваемостью учащихся действительно существует статистически достоверная зависимость. Однако по абсолютным значениям коэффициентов корреляции не всегда можно делать однозначные выводы о том, являются ли они значимыми, т.е. достоверно свидетельствуют о существовании зависимости между сравниваемыми переменными. Может случиться так, что коэффициент корреляции, равный 0,50, не будет достоверным, а коэффициент корреляции, составивший 0,30, — достоверным. Многое в решении этого вопроса зависит от того, сколько показателей было в коррелируемых друг с другом рядах признаков: чем больше таких показателей, тем меньшим по величине может быть статистически достоверный коэффициент корреляции. В табл. 35 представлены критические значения коэффициентов корреляции для различных степеней свободы. 1 Если исходные данные, которые ранжируются, одинаковы, то и их ранги также будут одинаковыми. Они получаются путем суммирования и деления пополам тех рангов, которые соответствуют этим данным. Таблица 35
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.013 с.) |

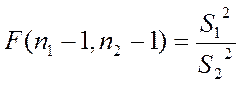
 — дисперсия по первой выборке;
— дисперсия по первой выборке; — дисперсия по второй выборке.
— дисперсия по второй выборке.
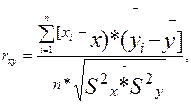

 — дисперсии, отклонения сравниваемых величин от
— дисперсии, отклонения сравниваемых величин от



