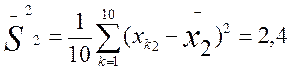Вопрос 2 методы вторичной статистической обработки результатов эксперимента

 

С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, до­казываются или опровергаются гипотезы, связанные с экспери­ментом.

Эти методы, как правило, сложнее, чем методы первич­ной статистической обработки, и требуют от исследователя хо­рошей подготовки в области элементарной математики и статис­тики.

Обсуждаемую группу методов можно разделить на несколь­ко подгрупп:

1. Регрессионное исчисление.
2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам.
3. Методы установления статистических взаимосвязей между пе­ременными, например их корреляции друг с другом.
4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ).

Рассмотрим каждую из выделенных подгрупп методов вторичной статистической обра­ботки на примерах.

1. Регрессионное исчисление — это метод математической ста­тистики, позволяющий свести частные, разрозненные данные к некоторому линейному графику, приблизительно отражающе­му их внутреннюю взаимосвязь, и получить возможность по зна­чению одной из переменных приблизительно оценивать вероят­ное значение другой переменной.

Воспользуемся для графического представления взаимосвязан­ных значений двух переменных х и у точками на графике (рис, 73). Поставим перед собой задачу: заменить точки на графике ли­нией прямой регрессии, наилучшим образом представляющей взаимосвязь, существующую между данными переменными. Иными словами, задача заключается в том, чтобы через скопле­ние точек, имеющихся на этом графике, провести прямую линию,

Рис. 73. Прямая регрессии Y no X. хср и уср — средние значения переменных. От­клонения отдельных значений от линии регрессии обозначены вертикальны­ми пунктирными линиями. Величина у,-у является отклонением измеренно­го значения переменной y_j от оценки, а величина у - у является отклонением оценки от среднего значения (Цит. по: Шерла К. Факторный анализ. М., 1980. С. 23).

 

пользуясь которой по значению одной из переменных, х или у, можно приблизительно судить о значении другой переменной. Для того чтобы решить эту задачу, необходимо правильно найти коэффициенты а и Ь в уравнении искомой прямой:

у = ах + b .

 

Это уравнение представляет прямую на графике и называет­ся уравнением прямой регрессии.

 

Формулы для подсчета коэффициентов а и Ь являются сле­дующими:

 

где х _i у _i- частные значения переменных X и Y, которым соответствуют точки на графике;

 

— средние значения тех же самых переменных;

 

п — число первичных значений или точек на графике.

 

Для сравнения выборочных средних величин, принадлежа­щих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, нередко используют t-критерий Стъюдента. Его основ­ная формула выглядит следующим образом:

где

х₁ — среднее значение переменной по одной выборке данных;

х₂ — среднее значение переменной по другой выборке данных;

т₁ и т₂ — интегрированные показатели отклонений частных значений из двух сравниваемых выборок от соответствующих им средних величин.

т₁ и т₂ в свою очередь вычисляются по следующим формулам:

 

 

где — выборочная дисперсия первой переменной (по первой выборке);

— выборочная дисперсия второй переменной (по второй выборке);

п_] — число частных значений переменной в первой выборке;

п₂ — число частных значений переменной по второй выборке.

 

После того как при помощи приведенной выше формулы вы­числен показатель t, по таблице 32 для заданного числа степеней свободы, равного n₁ + п₂ - 2, и избранной вероятности допусти­мой ошибки¹ находят нужное табличное значение t и сравнива-

¹ Степени свободы и вероятность допустимой ошибки — специальные математико-статистические термины, содержание которых мы здесь не будем рас­сматривать.

Таблица 32

Критические значения t-критерия Стъюдента

для заданного числа степеней свободы и вероятностей допустимых ошибок, равных 0,05; 0,01 и 0,001

 

Число степеней свободы (n1+ n2 -2)	Вероятность допустимой ошибки
0,05	0,01	0,001
Критические значения показателя t
	2,78	5,60	8,61
	2,58	4,03	6,87
	2,45	3,71	5,96
	2,37	3,50	5,41
	2,31	3,36	5,04
	2,26	3,25	4,78
	2,23	3,17	4,59
	2,20	3,11	4,44
	2,18	3,05	4,32
	2,16	3,01	4,22
	2,14	2,98	4,14
	2,13	2,96	4,07
	2,12	2,92	4,02
	2,11	2,90	3,97
	2,10	2,88	3,92
	2,09	2,86	3,88
	2,09	2,85	3,85
	2,08	2,83	3,82
	2,07	2,82	3,79
	2,07	2,81	3,77
	2,06	2,80	3,75
	2,06	2,79	3,73
	2,06	2,78	3,71
	2,05	2,77	3,69
	2,05	2,76	3,67
	2,05	2,76	3,66
	2,04	2,75	3,65
	2,02	2,70	3,55
	2,01	2,68	3,50
	2,00	2,66	3,46
	1,99	2,64	3,42
	1,98	2,63	3,39

ют с ними вычисленное значение t. Если вычисленное значение t больше или равно табличному, то делают вывод о том, что срав­ниваемые средние значения из двух выборок действительно статистически достоверно различаются с вероятностью допустимой ошибки, меньшей иди равной избранной. Рассмотрим процеду­ру вычисления t-критерия Стъюдента и определения на его ос­нове разницы в средних величинах на конкретном примере.

Допустим, что имеются следующие две выборки эксперимен­тальных данных: 2, 4, 5, 3, 2, 1, 3, 2, 6, 4 и 4, 5, 6, 4, 4, 3, 5, 2, 2, 7.

Средние значения по этим двум выборкам соответственно рав­ны 3,2 и 4,2. Кажется, что они существенно друг от друга отлича­ются. Но так ли это и насколько статистически достоверны эти различия? На данный вопрос может точно ответить только ста­тистический анализ с использованием описанного статистичес­кого критерия. Воспользуемся этим критерием.

Определим сначала выборочные дисперсии для двух срав­ниваемых выборок значений:

 

 

 

Поставим найденные значения дисперсий в формулу для под-

счета т и t и вычислим показатель t

Сравним его значение с табличным для числа степеней сво­боды 10+10-2 = 18. Зададим вероятность допустимой ошибки, равной 0,05, и убедимся в том, что для данного числа степеней свободы и заданной вероятности допустимой ошибки значение t должно быть не меньше чем 2,10. У нас же этот показатель ока­зался равным 1,47, т.е. меньше табличного. Следовательно, ги­потеза о том, что выборочные средние, равные в нашем случае 3,2 и 4,2, статистически достоверно отличаются друг от друга, не подтвердилась, хотя на первый взгляд казалось, что такие раз­личия существуют.

 

Вероятность допустимой ошибки, равная и меньшая чем 0,05, считается достаточной для научно убедительных выводов. Чем меньше эта вероятность, тем точнее и убедительнее делаемые вы­воды. Например, избрав вероятность допустимой ошибки, равную 0,05, мы обеспечиваем точность расчетов 95% и допускаем ошибку, не превышающую 5%, а выбор вероятности допустимой ошибки 0,001 гарантирует точность расчетов, превышающую 99,99%, или ошибку, меньшую чем 0,01%.

Описанная методика сравнения средних величин по крите­рию Стъюдента в практике применяется тогда, когда необходи­мо, например, установить, удался или не удался эксперимент, оказал или не оказал он влияние на уровень развития того пси­хологического качества, для изменения которого предназначал­ся. Допустим, что в некотором учебном заведении вводится но­вая экспериментальная программа или методика обучения, рас­считанная на то, чтобы улучшить знания учащихся, повысить уровень их интеллектуального развития. В этом случае выясня­ется причинно-следственная связь между независимой перемен­ной — программой или методикой и зависимой переменной — знаниями или уровнем интеллектуального развития. Соответ­ствующая гипотеза гласит: «Введение новой учебной програм­мы или методики обучения должно будет существенно улучшить знания или повысить уровень интеллектуального развития уча­щихся».

Предположим, что данный эксперимент проводится по схе­ме, предполагающей оценки зависимой переменной в начале и в конце эксперимента. Получив такие оценки и вычислив средние по всей изученной выборке испытуемых, мы можем воспользо­ваться критерием Стъюдента для точного установления нали­чия или отсутствия статистически достоверных различий меж­ду средними до и после эксперимента. Если окажется, что они действительно достоверно различаются, то можно будет сделать определенный вывод о том, что эксперимент удался. В против­ном случае нет убедительных оснований для такого вывода даже в том случае, если сами средние величины в начале и в конце эксперимента по своим абсолютным значениям различны.

Иногда в процессе проведения эксперимента возникает спе­циальная задача сравнения не абсолютных средних значений не­которых величин до и после эксперимента, а частотных, напри­мер процентных, распределений данных. Допустим, что для экс­периментального исследования была взята выборка из 100 учащихся и с ними проведен формирующий эксперимент. Предпо­ложим также, что до эксперимента 30 человек успевали на «удов­летворительно», 30 — на «хорошо», а остальные 40 — на «отлич­но». После эксперимента ситуация изменилась. Теперь на «удов­летворительно» успевают только 10 учащихся, на «хорошо» — 45 учащихся и на «отлично» — остальные 45 учащихся. Можно ли, опираясь на эти данные, утверждать, что формирующий экс­перимент, направленный на улучшение успеваемости, удался?

Для ответа на данный вопрос можно воспользоваться статис­тикой, называемой χ²-критерий («хи-квадрат критерий»). Его формула выглядит следующим образом:

где P_k —. частоты результатов наблюдений до эксперимента;

V_k — частоты результатов наблюдений, сделанных после экс­перимента;

т — общее число групп, на которые разделились результаты наблюдений.

 

Воспользуемся приведенным выше примером для того, что­бы показать, как работает хи-квадрат критерий. В данном при­мере переменная Р_к принимает следующие значения: 30%, 30%, 40%, а переменная V_k — такие значения: 10%, 45%, 45%.

 

Подставим все эти значения в формулу для %² и определим его величину:

 

Воспользуемся теперь таблицей 33, где для заданного числа степеней свободы можно выяснить степень значимости образо­вавшихся различий до и после эксперимента в распределении оценок. Полученное нами значение χ² — 21,5 больше соответст­вующего табличного значения т - 1 = 2 степеней свободы, со­ставляющего 13,82 при вероятности допустимой ошибки мень­ше чем 0,001. Следовательно, гипотеза о значимых изменениях, которые произошли в оценках учащихся в результате введения новой программы или новой методики обучения,

Таблица 33

Граничные (критические) значения c²-критерия,