
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод последовательного улучшения допустимого вектора (МПУ)Содержание книги
Поиск на нашем сайте
МПУ состоит в последовательном выполнении идентичных шагов (опишем вычислительные процедуры одного шага). К началу очередного шага пусть имеются некоторое ДБМ К и отвечающий ему допустимый вектор х (K) = (х1, х2,..., хп). Над этими исходными данными выполняются следующие процедуры: I. Определение вектора y (К). Зная базисные векторы
Эта система имеет единственное решение
Метод последовательного улучшения допустимого вектора (МПУ) II. Проверка двойственной допустимости ДБМ К. Для найденного вектора у (К) вычисляются величины 1. Находим величины При этом возможны два случая: а) б) условие а) нарушается, т.е. К не является двойственно допустимым и вектор Метод последовательного улучшения допустимого вектора (МПУ) III. Вычисление коэффициентов разложения вектора Для этого решаем систему уравнений IV. Определение (а) Все коэффициенты gk неположительные. Тогда на основании следствия 1 векторы Метод последовательного улучшения допустимого вектора (МПУ) IV. Определение (б) Среди коэффициентов gk разложения
При этом фиксируем элемент k* Метод последовательного улучшения допустимого вектора (МПУ)
V. Подготовка информации к следующему шагу. В качестве нового допустимого базисного множества принимаем K' = (K\ (k* }) Из базиса удаляется вектор
Вычисляем компоненты соответствующего вектора х (К') = ( по формулам
При этом
Метод последовательного улучшения допустимого вектора (МПУ) Замечание. В процедуре II, вообще говоря, нет необходимости вычислять
Метод последовательного улучшения допустимого вектора (МПУ) При решении задач с помощью МПУ исходная информация и текущие данные обычно располагают в таблицах следующего вида: Таблица 1. Исходная информация
Таблица 2. Текущие данные
Пример решения задачи ЛП с помощью МПУ Прямая задача А Двойственная задача А*
Найдем базис, базисное множество К, построим исходный допустимый вектор x (K)
Векторы α3, α4 – линейно независимы, базисное множество K ={3,4}.
Пример решения задачи ЛП с помощью МПУ I. Определение вектора y (К). Шаг Единственное решение имеет система:
II. Проверка двойственной допустимости ДБМ К
Пример решения задачи ЛП с помощью МПУ III. Вычисление коэффициентов разложения вектора
IV. Определение Определяем, какой вектор удалить из базиса.
Пример решения задачи ЛП с помощью МПУ V. Подготовка информации к следующему шагу. В качестве нового допустимого базисного множества принимаем
k
2 шаг …………………
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.144.73 (0.01 с.) |

 и допустимый базисный вектор
и допустимый базисный вектор 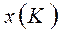 =(х1, х2,..., хm, 0,…,0), решаем систему линейных уравнений:
=(х1, х2,..., хm, 0,…,0), решаем систему линейных уравнений:
 , т.к. К – это базисное множество.
, т.к. К – это базисное множество.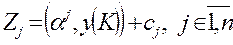 и проверяются неравенства
и проверяются неравенства  ,
, 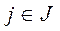 .
.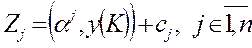

 . Это означает, что базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством. Тогда (потеореме: если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы
. Это означает, что базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством. Тогда (потеореме: если базисное множество К является одновременно допустимым и двойственно допустимым базисным множеством, то отвечающие ему векторы 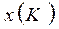 и
и 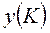 оптимальные соответственно в задачах А и А*) векторы х (К) и у (К) оптимальны для соответствующих задач и
оптимальные соответственно в задачах А и А*) векторы х (К) и у (К) оптимальны для соответствующих задач и  . На этом процесс заканчивается с выдачей искомых оптимальных векторов.
. На этом процесс заканчивается с выдачей искомых оптимальных векторов.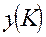 не допустимый в задаче А*. Надо найти
не допустимый в задаче А*. Надо найти 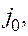
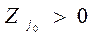 и перейти к выполнению следующей процедуры.
и перейти к выполнению следующей процедуры.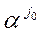 по базисным векторам.
по базисным векторам.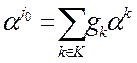 . Матрица этой системы совпадает с транспонированной матрицей системы, решаемой на процедуре 1, поэтому она также имеет единственное решение. В результате определяем
. Матрица этой системы совпадает с транспонированной матрицей системы, решаемой на процедуре 1, поэтому она также имеет единственное решение. В результате определяем 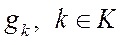
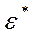 . Проверяем выполнение неравенств
. Проверяем выполнение неравенств 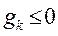 ,
,  . При этом возможны два случая.
. При этом возможны два случая.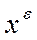 , определяемые в лемме 3, являются допустимыми в задаче А при всех
, определяемые в лемме 3, являются допустимыми в задаче А при всех  , а линейная функция
, а линейная функция 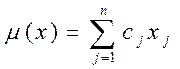 на множестве таких векторов не ограничена сверху. Процесс на этом заканчивается с выдачей вектора х(К) и коэффициентов gk.
на множестве таких векторов не ограничена сверху. Процесс на этом заканчивается с выдачей вектора х(К) и коэффициентов gk.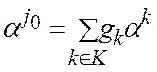 имеются положительные. Тогда на основании следствие 2 векторы
имеются положительные. Тогда на основании следствие 2 векторы  являются допустимыми в задаче А лишь при
являются допустимыми в задаче А лишь при 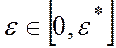 , где
, где 
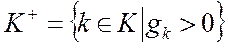 .
. K*, на котором достигается равенство
K*, на котором достигается равенство  , затем переходим к последней процедуре.
, затем переходим к последней процедуре.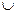 { j0 }.
{ j0 }.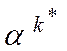 , а вводится в базис вектор
, а вводится в базис вектор  .
.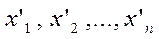 )
) , k
, k 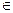 K' \ { j0 },
K' \ { j0 }, 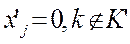 .
.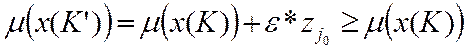 .
.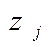 для всех
для всех  . Естественно, для каждой вычисленной величины
. Естественно, для каждой вычисленной величины 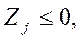
 . Если это неравенство нарушается, то имеет место случай б), т.е. К не является двойственно допустимым и вектор
. Если это неравенство нарушается, то имеет место случай б), т.е. К не является двойственно допустимым и вектор 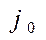 можно принять соответствующее
можно принять соответствующее 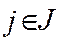 . Однако ввиду того, что
. Однако ввиду того, что 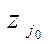 должно быть не очень малым. Поэтому при решении небольших задач обычно вычисляют все величины
должно быть не очень малым. Поэтому при решении небольших задач обычно вычисляют все величины 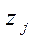 и в случае б) индекс
и в случае б) индекс 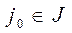 выбирается так, чтобы
выбирается так, чтобы  . При решении больших задач все
. При решении больших задач все 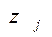 уже не вычисляются, но с помощью специальных приемов добиваются того, чтобы для выбранного
уже не вычисляются, но с помощью специальных приемов добиваются того, чтобы для выбранного 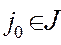 в случае б) величина
в случае б) величина 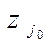 мало отличалась от максимального
мало отличалась от максимального 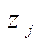 .
.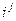
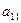
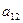
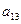

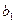
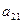
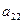
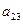
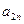
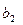

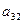
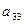



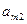
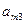




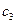




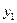
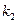
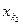
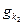
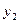
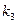

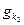



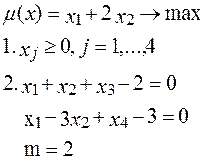
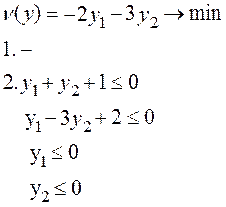
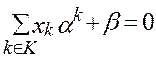 - имеет единственное решение
- имеет единственное решение
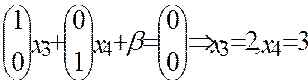

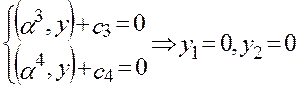 y (K)=(0,0)
y (K)=(0,0)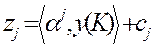 ,
, 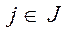 .
.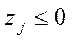 ,
, 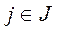 ?
?
 Ясно, что
Ясно, что 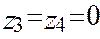
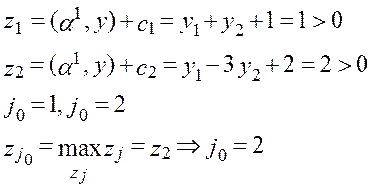
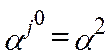 вводим в базис
вводим в базис
 по базисным векторам.
по базисным векторам.
 Т.к.
Т.к. 
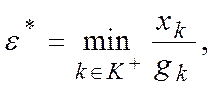

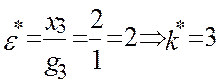 Исключаем из базиса вектор
Исключаем из базиса вектор 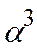
 K' = (K\ (k* })
K' = (K\ (k* }) 
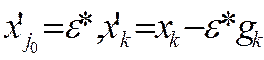 ,
, 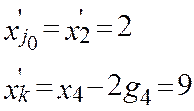
 - допустимый вектор
- допустимый вектор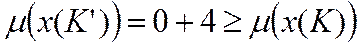 (функция не ухудшилась)
(функция не ухудшилась)


