Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак оптимальности в краткой формеСодержание книги Поиск на нашем сайте Для оптимальности допустимого вектора х= (х1,х2, …хn,) в задаче 1 достаточно существования допустимого вектора y= (y1,y2,…..yn) в задаче 1*, удовлетворяющего условию m (х) = n (у)(16) Тогда допустимый вектор y= (y1,y2,…..yn) также является оптимальным в задаче 1*.
Доказательство. Пусть вектор х допустимый и существует допустимый вектор у такой, что справедливо (16). Покажем, вектор х оптимальный. Рассмотрим некоторый другой оптимальный вектор х′ в задаче 1 (х′≠х), тогда имеем пару векторов х′ и у. Для этой пары допустимых векторов справедлива лемма 1, т. е. m (х′) ≤ n (у) =m (х)и m (х′) ≤m (х). Отсюда следует что х – оптимальный вектор. Покажем теперь, что вектор у также является оптимальным. Рассмотрим некоторый другой оптимальный вектор у′ в задаче 1 (у′≠у), тогда имеем пару векторов х и у′. Для этой пары допустимых векторов справедливо лемма 1, т. е. n(у′)≥m(х)= n(у) и n(у)≤ n(у′). Отсюда следует что у – оптимальный вектор.▄ Признак оптимальности в развернутой форме
Для оптимальности допустимого вектора х= (х1,х2…,хn,) в задаче 1 достаточно существование m-мерного вектора у =(у1,у2,у3,…,уm), удовлетворяющего условиям: а) уi і 0, iОI2 б) еaijyi + cj = 0, jОJ1, iОI в) еaijyi + cj, £ 0, jОJ2, iОI г) еaijyi + cj, = 0, если хj >0 для jОJ2, iОI д) уi = 0, если еaijxj + bi >0, iОI2, jОJ тогда вектор у является оптимальным в задаче 1*.
Пример применения признака оптимальности в развернутой форме
Как этим признаком пользоваться? Предположим, что мы имеем допустимый вектор х, т.е. хj ≥0 и такие, что Тогда попытаемся найти вектор у из уравнений б), г), д). Эта система совместна и имеет единственное решение, если выполняются следующие условия: 1) Количество уравнений в системе m (совпадает с числом переменных); 2) Матрицы при неизвестных – неособенные
Пример применения признака оптимальности в развернутой форме
Пример применения признака оптимальности в развернутой форме
Пример применения признака оптимальности в развернутой форме
Основная теорема теории линейного программирования И ее следствия Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум). Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев. 1. В задачах 1 и 1* имеются оптимальные векторы х и у и 2. В задаче 1 существуют допустимые векторы х из некоторого множества Х, но линейная функция 3. В задаче 1* существуют допустимые векторы 4. В задачах 1 и 1* нет допустимых векторов, то есть
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

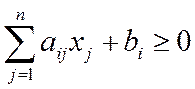 ,
,  .
.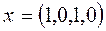 на оптимальность в следующей задаче ЛП:
Максимизировать
на оптимальность в следующей задаче ЛП:
Максимизировать
 при условиях:
при условиях:

 .
Подставляя значения компонент вектора в ограничении I0 и 20, убеждаемся, что все они выполняются. Для проверки остальных условий признака оптимальности составляем двойственную задачу:
Требуется найти вектор
.
Подставляя значения компонент вектора в ограничении I0 и 20, убеждаемся, что все они выполняются. Для проверки остальных условий признака оптимальности составляем двойственную задачу:
Требуется найти вектор 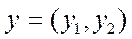 , удовлетворяющий условиям:
, удовлетворяющий условиям:
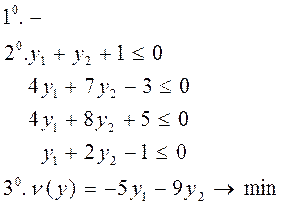
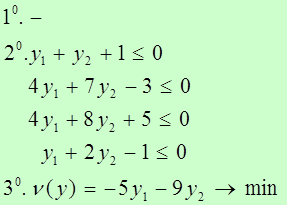
 I – условие г)
Запишем условие г) признака оптимальности:
I – условие г)
Запишем условие г) признака оптимальности:
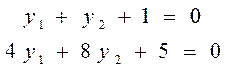 (т.к.
(т.к. 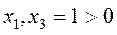 , следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
, следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
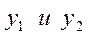 .
.
 Найден вектор
Найден вектор  . Проверяем его допустимость в двойственной задаче, т.е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т.к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х =(1, 0, 1, 0)- оптимальным в основной задаче.
. Проверяем его допустимость в двойственной задаче, т.е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т.к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х =(1, 0, 1, 0)- оптимальным в основной задаче.
 , т.е. обе задачи разрешимы.
, т.е. обе задачи разрешимы.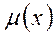 на множестве этих векторов не ограничена сверху, т.е.
на множестве этих векторов не ограничена сверху, т.е. 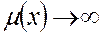 , тогда в задаче 1* нет допустимых векторов.
, тогда в задаче 1* нет допустимых векторов. , но функция
, но функция 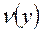 не ограничена снизу на множестве этих векторов, т.е.
не ограничена снизу на множестве этих векторов, т.е. 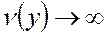 , тогда в задаче 1 нет допустимых векторов.
, тогда в задаче 1 нет допустимых векторов.