
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача математического программированияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
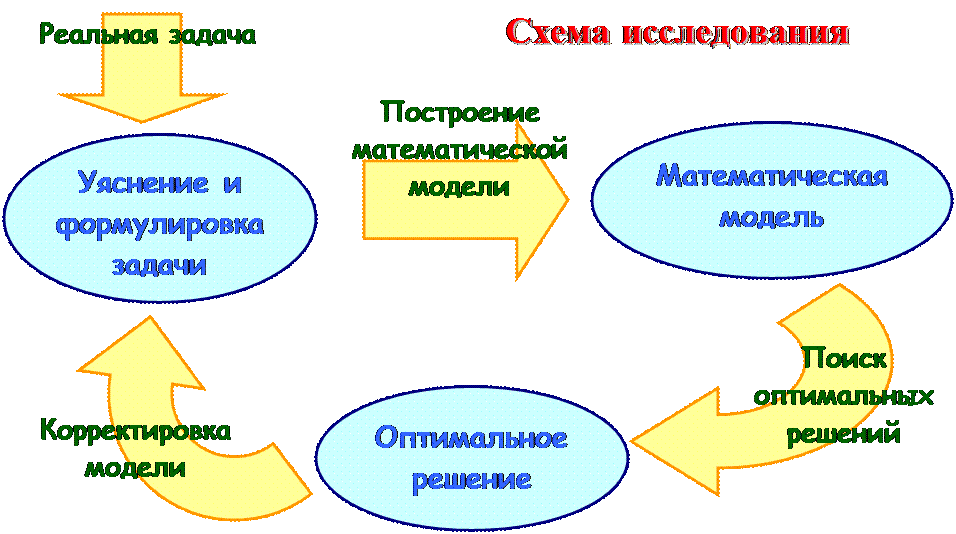
Методы оптимизации
Математическая модель Математическая модель — описание решаемой задачи в математических терминах. Математическая модель описывает исследуемую систему и позволяет выразить ее эффективность в виде целевой функции W = f (X, Y), где X = (x 1,…, xn) — управляемые переменные, Y = (y 1,…, y m) — неуправляемые переменные(исходные данные). Связь между переменными X и исходными данными Y выражается с помощью ограничений j (X, Y) £ 0. Виды моделей · детерминированные; · вероятностные; · игровые; · неполные (задачи в условиях неопределенности).
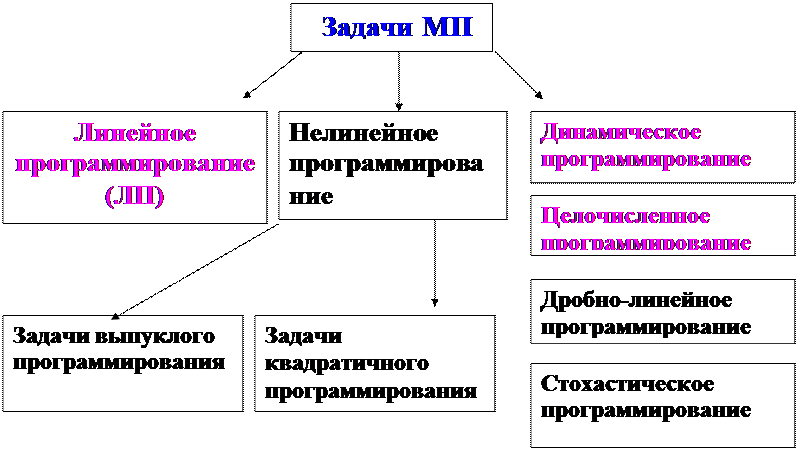
Исследованием детерминированных моделей занимается математическое программирование (МП).
Термин «программирование» означает «поиск наилучших планов» (programming – планирование – составление плана или программы действий).
Задача оптимизации
(
Задача математического программирования
Оптимальным решением задачи (минимизации) называют допустимое решение, минимизирующее f (x) на множестве всех допустимых решений. Задачи математического программирования
История математического программирования Б.Т. Поляк, Институт проблем управления, Москва История математического программирования в СССР: попытка анализа
История математического программирования 1. Леонард Эйлер, 1707-1783, первый ученый, занимавшийся оптимизацией в России 2. Чебышев П.Л., 1821-1894, основы выпуклой оптимизации, решал практические оптимизационные задачи: построение наименее искаженной географической карты, оптимальный раскрой, наилучший выбор параметров механических устройств 3. А.А. Марков, 1856-1922, известны работы в теории чисел и теории вероятностей (Марковские цепи, Марковские процессы) 4. А.М. Ляпунов, 1857-1918, разработал теорию устойчивости для дифференциальных обыкновенных уравнений, тем самым внес огромный вклад в развитие непрерывной оптимизации, предложил инструмент для проверки сходимости численных методов оптимизации История математического программирования 5. Л.В. Канторович, 1912-1986, в 1975г. получил Нобелевскую премию в области экономики, один из основателей численного анализа в нашей стране, одним из первых признал информатику как новую ветвь в математике.
Отец новой науки ОПТИМИЗАЦИИ, которая включает стандартное математическое программирование. С именем Канторовича Л.В.связаны следующие достижения: Линейное программирование, 1939: Опубликована книга (67 стр.), в которой рассматривался новый тип оптимизационных задач. Формы записи этих задач были иными, чем стандартная формулировка задачи ЛП, причем модель, рассматриваемая в западной литературе - частный случай модели Канторовича. Общие условия оптимальности, 1940 Техника функционального анализа, 1939-1948
История математического программирования 6. Г.Ш. Рубинштейн, ученик Канторовича Л.В., учитель д.т.н., проф. УГАТУ Мухачевой Э.А. В 1961г. вышла книга Канторовича Л.В. и Рубинштейна Г.Ш., в которой давались математические формулировки задачи ЛП и приводились численные методы ее решения, были введены понятия двойственных переменных, которые назывались «объектно-обусловленными оценками». 7. В 50-е годы – интенсивные исследования в области ЛП. Стали известны работы западных ученых: Дж. Данцига, Г.Куна, А. Таккера и др. по ЛП. Выпущен первый учебник на русском языке по ЛП Юдиным Д.Б., Гольштейном Е.Г. 8. 60-е годы Появилась общая теория двойственности для задач выпуклой оптимизации (Гольштейн Е.Г.), появились труды по стохастической оптимизации. Литература 1.Канторович Л.В. Математические методы организации и планирования производства. Л.: Изд-во Ленинградский университет, 1939, 64с. 2. Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. М.: Советское радио. 1964, 491с. 3. Карманов В.Г. Математическое программирование. М.: Наука, 1975, 272с. 4. Мухачева Э.А., Рубинштейн Г.Ш. Математическое программирование. Новосибирск: Изд-во «Наука», Сибирское отделение, 1987, 272с. 5. Мухачева Э.А. Рациональный раскрой промышленных материалов. Применение АСУ. М.: Машиностроение, 1984,174с. 6. Мухачева Э.А., Верхотуров М.А., Мартынов В.В. Модели и методы расчета раскроя-упаковки геометрических объектов. Уфа: УГАТУ, 1998, 217с. 7. Мухачева Э.А., Валеева А.Ф., Картак В.М. Задачи двухмерной упаковки в контейнеры: новые подходы к разработке методов локального поиска оптимума. Москва: Изд-во МАИ, 2004, 192с.
Задача об оптимальной смеси
Общая форма задачи ЛП Пусть заданы: множества I ={1,2…m} и J= {1,2…n}, причем I= I1U I2, I1 Ç I2 = Æ, J= J1UJ2, J1Ç J2 = Æ, вещественные числа аij, iÎI, jÎJ; bi, iÎI, сj, jÎJ.
ЗАДАЧА 1 (прямая со смешанными ограничениями) Максимизировать линейную функцию
на множестве векторов х= (х1,х2, …хn,), (2) удовлетворяющих условиям:
1. хj ³0 для jÎJ2 (3) 2.
Двойственная задача ЛП ЗАДАЧА 1* (двойственная со смешанными ограничениями). Минимизировать линейную функцию
на множестве векторов y= (y1,y2,…..ym), (6) удовлетворяющих условиям: 1. yi ≥ 0 для iÎI2 (7) 2.
Определение. Векторы (2), (6), удовлетворяющие условиям (3), (4) и (7), (8) называются допустимым для задачи 1 и задачи 1* соответственно. Допустимые векторы (2), (6), доставляющие максимум функции (1) и минимум функции (5) соответственно, называются оптимальными. Пример составления двойственной задачи ЛП
Пример составления двойственной задачи ЛП
Связь между задачами 1 и 1*
Связь между парой двойственных задач устанавливает следующая лемма 1: Для любых допустимых векторов х и у в задачах 1 и 1* выполняются неравенства µ(x) £ причем (9) выполняется как равенство в том и только в том случае, если справедливы следующие соотношения:
Связь между задачами 1 и 1* Доказательство. Имеем:
Связь между задачами 1 и 1* Доказательство (продолжение). Имеем:
yi ≥ 0 для iÎI2
Правые части в соотношениях (13) и (15) отличаются лишь порядком суммирования и, следовательно, равны между собой, т.е. выполняется µ(x) £
Доказательство. Пусть вектор х допустимый и существует допустимый вектор у такой, что справедливо (16). Покажем, вектор х оптимальный. Рассмотрим некоторый другой оптимальный вектор х′ в задаче 1 (х′≠х), тогда имеем пару векторов х′ и у. Для этой пары допустимых векторов справедлива лемма 1, т. е. m (х′) ≤ n (у) =m (х)и m (х′) ≤m (х). Отсюда следует что х – оптимальный вектор. Покажем теперь, что вектор у также является оптимальным. Рассмотрим некоторый другой оптимальный вектор у′ в задаче 1 (у′≠у), тогда имеем пару векторов х и у′. Для этой пары допустимых векторов справедливо лемма 1, т. е. n(у′)≥m(х)= n(у) и n(у)≤ n(у′). Отсюда следует что у – оптимальный вектор.▄ Пример применения признака оптимальности в развернутой форме
Как этим признаком пользоваться? Предположим, что мы имеем допустимый вектор х, т.е. хj ≥0 и такие, что Тогда попытаемся найти вектор у из уравнений б), г), д). Эта система совместна и имеет единственное решение, если выполняются следующие условия: 1) Количество уравнений в системе m (совпадает с числом переменных); 2) Матрицы при неизвестных – неособенные
Пример применения признака оптимальности в развернутой форме
Пример применения признака оптимальности в развернутой форме
Пример применения признака оптимальности в развернутой форме
И ее следствия Для разрешимости задачи математического программирования (как и в любой оптимизационной задачи) необходимо, чтобы множество допустимых решений было не пусто, и целевая функция на этом множестве была ограничена сверху (если задача на максимум), либо снизу (если задача на минимум). Теорема двойственности. Каковы бы ни были исходные данные, для задач 1 и 1* имеет место один из следующих взаимоисключающих случаев. 1. В задачах 1 и 1* имеются оптимальные векторы х и у и 2. В задаче 1 существуют допустимые векторы х из некоторого множества Х, но линейная функция 3. В задаче 1* существуют допустимые векторы 4. В задачах 1 и 1* нет допустимых векторов, то есть Базисное множество
Пусть Множество К называют базисным множеством, если отвечающие ему векторы
на множестве n -мерных векторов х = (х1, х2,..., хn), удовлетворяющих условиям 1. 2. Пример. Векторы Лемма 2 Каково бы ни было базисное множество K, для соответствующих векторов х (К) и у (К) имеет место равенство
Доказательство. Так как
что и требовалось показать.▄
Лемма 3 Пусть задано некоторое базисное множество К и отвечающий ему вектор х (К) = (х1, х2,..., хп). Кроме того, для некоторого
Тогда при любом
удовлетворяет условию
Лемма 3 Доказательство. Имеем: После умножения соотношения (18) на Имеем: Складывая (19) и (20), получаем
Следовательно, интересующий нас вектор
Следствие 1 из леммы 3 Вектор Возможны два случая: а). Все коэффициенты gk≤ 0 в б) среди коэффициентов gk имеются положительные Следствие 1. Если имеет место случай а),то векторы Действительно,
По теореме двойственности (слайд 42) в двойственной задаче допустимый вектор не существует, следовательно, вектор х не оптимальный ▄
Следствие 2 из леммы 3 Вектор Случай б) среди коэффициентов gk имеются положительные Следствие 2. Если имеет место случай б),то векторы
причем
Пусть V. Подготовка информации к следующему шагу. В качестве нового допустимого базисного множества принимаем K' = (K\ (k* }) Из базиса удаляется вектор
Вычисляем компоненты соответствующего вектора х (К') = ( по формулам
При этом
Пример решения задачи ЛП с помощью МПУ Прямая задача А Двойственная задача А*
Найдем базис, базисное множество К, построим исходный допустимый вектор x (K)
Векторы α3, α4 – линейно независимы, базисное множество K ={3,4}.
Пример решения задачи ЛП с помощью МПУ I. Определение вектора y (К). Шаг Единственное решение имеет система:
II. Проверка двойственной допустимости ДБМ К
Пример решения задачи ЛП с помощью МПУ III. Вычисление коэффициентов разложения вектора
IV. Определение Определяем, какой вектор удалить из базиса.
Пример решения задачи ЛП с помощью МПУ V. Подготовка информации к следующему шагу. В качестве нового допустимого базисного множества принимаем
k
2 шаг ………………… Методы оптимизации
Математическая модель Математическая модель — описание решаемой задачи в математических терминах. Математическая модель описывает исследуемую систему и позволяет выразить ее эффективность в виде целевой функции W = f (X, Y), где X = (x 1,…, xn) — управляемые переменные, Y = (y 1,…, y m) — неуправляемые переменные(исходные данные). Связь между переменными X и исходными данными Y выражается с помощью ограничений j (X, Y) £ 0. Виды моделей · детерминированные; · вероятностные; · игровые; · неполные (задачи в условиях неопределенности).
Исследованием детерминированных моделей занимается математическое программирование (МП).
Термин «программирование» означает «поиск наилучших планов» (programming – планирование – составление плана или программы действий).
Задача оптимизации
(
Задача математического программирования
Оптимальным решением задачи (минимизации) называют допустимое решение, минимизирующее f (x) на множестве всех допустимых решений.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.145.198 (0.015 с.) |


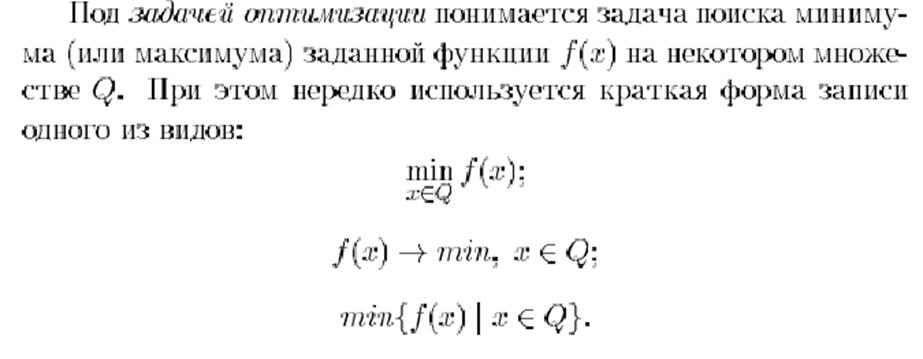
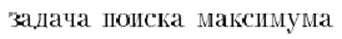
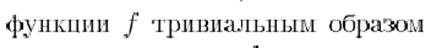
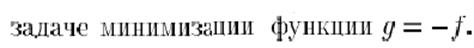 )
)
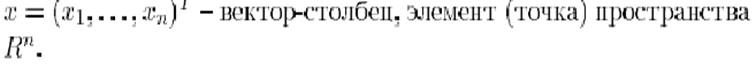




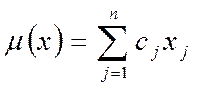 (1)
(1)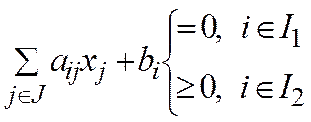 (4)
(4)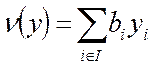 (5)
(5)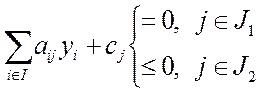 (8)
(8)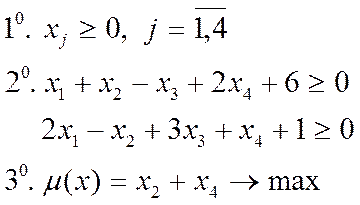
 т.е все переменные связаны условием неотрицательности, и все ограничения выполняются как неравенства. Двойственная задача имеет вид:
ЗАДАЧА 1*
Найти
т.е все переменные связаны условием неотрицательности, и все ограничения выполняются как неравенства. Двойственная задача имеет вид:
ЗАДАЧА 1*
Найти 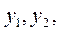 удовлетворяющие условиям:
удовлетворяющие условиям:
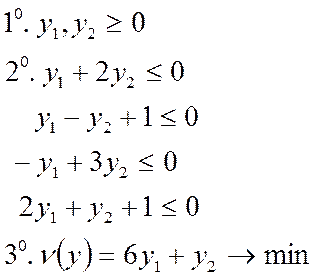
 =2x1 — х2 + Зх3 + х4 — 5x5
на множестве пятимерных векторов
х = (х1, х2, х3, х4, х5),
удовлетворяющих условиям
=2x1 — х2 + Зх3 + х4 — 5x5
на множестве пятимерных векторов
х = (х1, х2, х3, х4, х5),
удовлетворяющих условиям
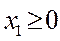 ,
,  ,
, 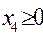 ,
Зх1 + 2х2 - 5х3 + х5 - 7
,
Зх1 + 2х2 - 5х3 + х5 - 7  0,
3х2 - 4х3 - 2х4 + 1 = 0,
2х1 + 2х3 - 3х4 + х5
0,
3х2 - 4х3 - 2х4 + 1 = 0,
2х1 + 2х3 - 3х4 + х5 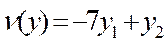 на множестве трехмерных векторов, удовлетворяющих условиям
на множестве трехмерных векторов, удовлетворяющих условиям
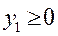 ,
, 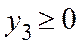 ,
3y1 + 2y3 + 2
,
3y1 + 2y3 + 2  0,
2y1 + 3y2 -1 = 0,
- 5y1 + 4y2 + 3y3 + 3
0,
2y1 + 3y2 -1 = 0,
- 5y1 + 4y2 + 3y3 + 3  (у), (9)
(у), (9) (10)
(10)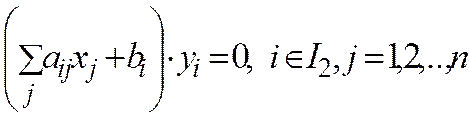 (11)
(11)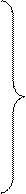 хj ³0 для jÎJ2
хj ³0 для jÎJ2
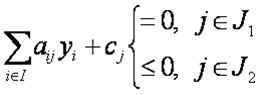
 (12)
(12) Суммируя полученные соотношения, получим с учетом того, что
Суммируя полученные соотношения, получим с учетом того, что  (13)
(13)

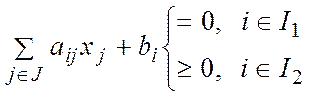

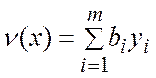
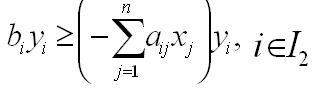 (14)
(14)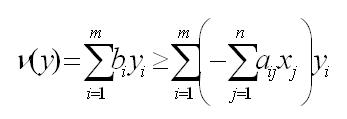 (15)
(15)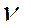 (у) (9). Для достижения равенства в (9), очевидно, необходимо и достаточно, чтобы достигались равенства во всех неравенствах (13) и (15). Последнее эквивалентно выполнению соотношений (10) и (11) ▄
(у) (9). Для достижения равенства в (9), очевидно, необходимо и достаточно, чтобы достигались равенства во всех неравенствах (13) и (15). Последнее эквивалентно выполнению соотношений (10) и (11) ▄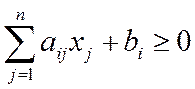 ,
,  .
.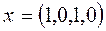 на оптимальность в следующей задаче ЛП:
Максимизировать
на оптимальность в следующей задаче ЛП:
Максимизировать
 при условиях:
при условиях:

 .
Подставляя значения компонент вектора в ограничении I0 и 20, убеждаемся, что все они выполняются. Для проверки остальных условий признака оптимальности составляем двойственную задачу:
Требуется найти вектор
.
Подставляя значения компонент вектора в ограничении I0 и 20, убеждаемся, что все они выполняются. Для проверки остальных условий признака оптимальности составляем двойственную задачу:
Требуется найти вектор 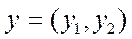 , удовлетворяющий условиям:
, удовлетворяющий условиям:
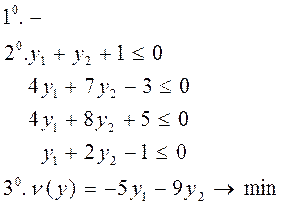
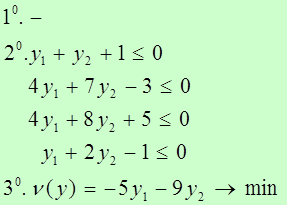
 I – условие г)
Запишем условие г) признака оптимальности:
I – условие г)
Запишем условие г) признака оптимальности:
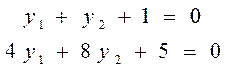 (т.к.
(т.к. 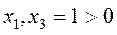 , следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
, следовательно, в первом и третьем ограничении условия 20 двойственной задачи достигается равенство)
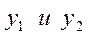 .
.
 Найден вектор
Найден вектор  . Проверяем его допустимость в двойственной задаче, т.е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т.к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х =(1, 0, 1, 0)- оптимальным в основной задаче.
. Проверяем его допустимость в двойственной задаче, т.е. выясняем, выполняются ли условия I0 и 20 двойственной задачи. Т.к. все условия выполняются, вектор y является оптимальным в двойственной задаче, а вектор х =(1, 0, 1, 0)- оптимальным в основной задаче.
 , т.е. обе задачи разрешимы.
, т.е. обе задачи разрешимы.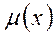 на множестве этих векторов не ограничена сверху, т.е.
на множестве этих векторов не ограничена сверху, т.е. 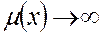 , тогда в задаче 1* нет допустимых векторов.
, тогда в задаче 1* нет допустимых векторов. , но функция
, но функция 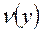 не ограничена снизу на множестве этих векторов, т.е.
не ограничена снизу на множестве этих векторов, т.е. 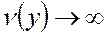 , тогда в задаче 1 нет допустимых векторов.
, тогда в задаче 1 нет допустимых векторов.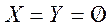
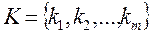 – m -мерное подмножество множества J.
– m -мерное подмножество множества J.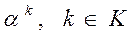 являются линейно независимыми, т.е. образуют базис в пространстве Rm. Число векторов в базисном множестве К равно числу m уравнений в условии 2 задачи А:
являются линейно независимыми, т.е. образуют базис в пространстве Rm. Число векторов в базисном множестве К равно числу m уравнений в условии 2 задачи А: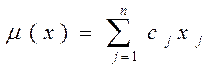 → max
→ max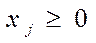 ,
, 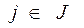 ,
,
 - линейно независимые, т.к.
- линейно независимые, т.к.  , К= { 1,2 }.
, К= { 1,2 }. .
. ,
,  ,
,  ,
, 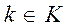 ,
, 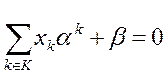 получаем
получаем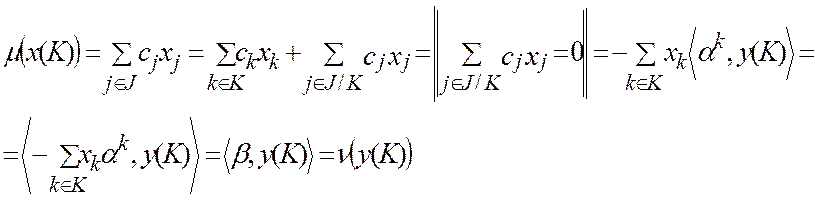 ,
,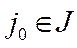 известны коэффициенты gk в разложении вектора
известны коэффициенты gk в разложении вектора 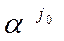 посоответствующим базисным векторам:
посоответствующим базисным векторам: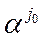 =
= 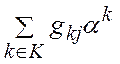 .
.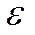 вектор
вектор 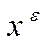 = (
= (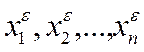 ) с компонентами
) с компонентами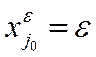 ,
, 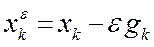 ,
,  ,
, 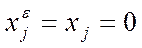 ,
, 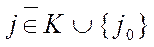 ,
, , причем значение линейной функции
, причем значение линейной функции 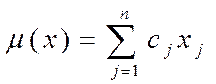 на этом векторе может быть вычислено по формуле
на этом векторе может быть вычислено по формуле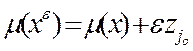 ,где величина
,где величина 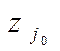 определяется из системы
определяется из системы  ,
, 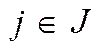 .
.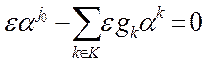 (24)
(24) . (26)
. (26)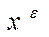 удовлетворяет требуемому условию
удовлетворяет требуемому условию 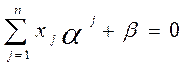 . Далее, для вектора
. Далее, для вектора 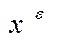 выполнены равенства (в силу того, что
выполнены равенства (в силу того, что  ,
, 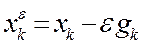 ,
, 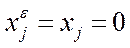 ,
,  и (22))
и (22))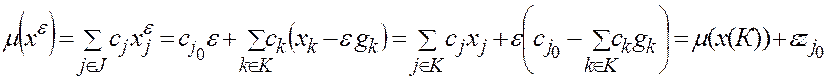 (27) ▄
(27) ▄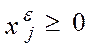 .
.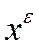 , определяемые в лемме 3, являются допустимыми в задаче А при всех
, определяемые в лемме 3, являются допустимыми в задаче А при всех  , а линейная функция
, а линейная функция 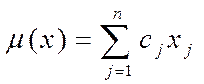 на множестве таких векторов не ограничена сверху.
на множестве таких векторов не ограничена сверху.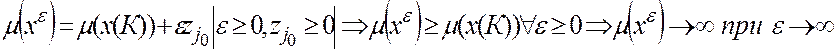
 являются допустимыми в задаче А лишь при
являются допустимыми в задаче А лишь при 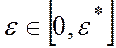 , где
, где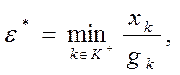
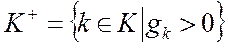 ,
,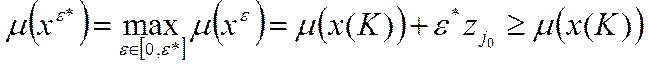 .
. ;
;  выполняется всегда;
выполняется всегда; 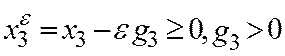 . Тогда
. Тогда 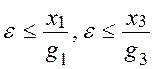 , чтобы эти неравенства выполнялись одновременно, находят
, чтобы эти неравенства выполнялись одновременно, находят 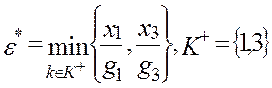
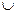 { j0 }.
{ j0 }.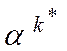 , а вводится в базис вектор
, а вводится в базис вектор  .
.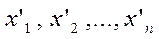 )
) , k
, k 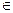 K' \ { j0 },
K' \ { j0 }, 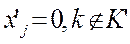 .
.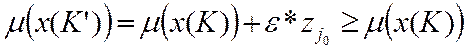 .
.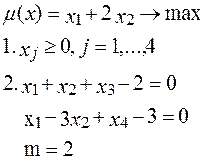
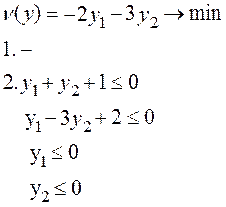
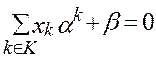 - имеет единственное решение
- имеет единственное решение
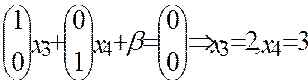
 , K ={3,4}.
, K ={3,4}.
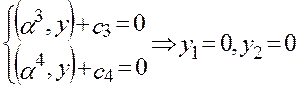 y (K)=(0,0)
y (K)=(0,0)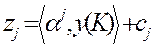 ,
, 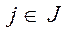 .
.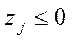 ,
, 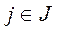 ?
?
 Ясно, что
Ясно, что 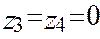
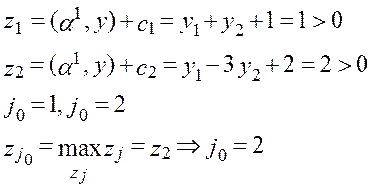
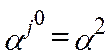 вводим в базис
вводим в базис
 по базисным векторам.
по базисным векторам.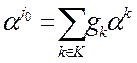 - разложение по базису
- разложение по базису
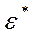 .
. Т.к.
Т.к. 
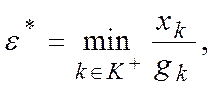

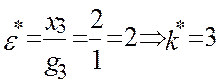 Исключаем из базиса вектор
Исключаем из базиса вектор 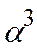
 K' = (K\ (k* })
K' = (K\ (k* }) 
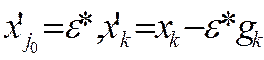 ,
, 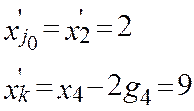
 - допустимый вектор
- допустимый вектор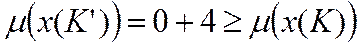 (функция не ухудшилась)
(функция не ухудшилась)


