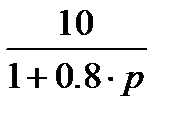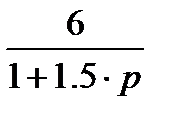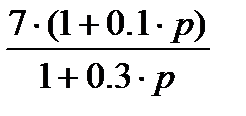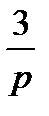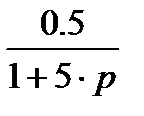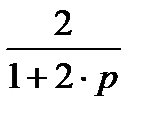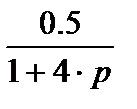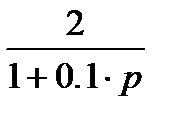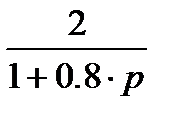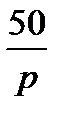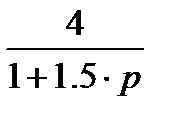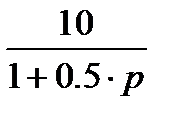Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость замкнутой импульсной системы и ее предельный коэффициентСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определим устойчивость замкнутой САУ и предельный коэффициент усиления ( По критерию Найквиста: Так как АФХ Предельный коэффициент можно определить согласно следующему соотношению:
где По критерию Гурвица: Запишем передаточную функцию дискретной САУ в замкнутом состоянии через Z–преобразование (относительно сигнала y):
Введем подстановку
После преобразований, из последнего соотношения получим:
Так как характеристическое уравнение устойчивой системы 3-го порядка имеет все положительные коэффициенты, то рассматриваемая система является неустойчивой в замкнутом состоянии. Определим
Тогда соответствующая передаточная функция САУ в замкнутом состоянии
Подставим в характеристическое уравнение соответствующее передаточной функции
Так как для САУ 3-го порядка условие устойчивости сводится к положительности коэффициентов характеристического уравнения и выполнению неравенства a1*a2-a0*a3>0, где a0= a2= то из коэффициента при старшей степени получаем На основе необходимого и достаточного условия устойчивости системы (в плоскости “Z”): Найдем корни характеристического уравнения замкнутой системы:
Корни, равные (-46,986; 0,9790; 0,9907) выходят из окружности единичного радиуса, значит, замкнутая система неустойчива. Возьмем Для
Откуда корни характеристического уравнения для замкнутой системы равны:
Переходной процесс на выходе замкнутой ИСАУ (xp(t)) Построим переходной процесс на выходе замкнутой импульсной САУ xp(t) при
Для этого найдем дискретную передаточную функцию прямой цепи заданной системы, т.е.
Запишем эту передаточную функцию относительно аргумента z и разделим числитель и знаменатель
Переходной процесс можно построить по следующему разностному уравнению, полученному из выражения для
Рис. 18
Кинетическая и статическая ошибки замкнутой ИСАУ (xуст=xy-y): Передаточная функция системы относительно ошибки равна:
Тогда статистическая ошибка при
Кинетическая ошибка имеет место, когда входной является функция, изменяющаяся по линейному закону:
Дискретное преобразование Лапласа указанного сигнала:
С учетом этого кинетическая ошибка будет равна:
Моделирование Импульсной САУ в Matlab (Simulink) Смоделируем импульсную систему в Matlab (Simulink). Схема модели представлена на рис. 19, а переходная функция - на рис.20.
Рис.19
Рис.20 Сравнение рис.18 и 20 показывает, что сигналы на выходе системы в дискретные моменты времени совпадают, что подтверждает правильность расчетов.
Варианты расчетных заданий Для каждого из указанных в таблице 2 вариантов необходимо: 1. Преобразовать исходную структурную схему к типовому виду (Рис. 7); определить непрерывную передаточную функцию приведенной непрерывной части разомкнутой импульсной системы 2. По 3. Построить годограф разомкнутой импульсной САУ: a) По выражению b) По выражению годографа Период работы импульсного элемента Ти=0,01с 4. Оценить устойчивость замкнутой импульсной САУ и найти предельный коэффициент усиления: a) По критерию Найквиста; b) По критерию Гурвица; c) По корням характеристического уравнения 5. Построить переходной процесс для замкнутой импульсной САУ (относительно выходного сигнала Xp(t). 6. Определить статическую и кинетическую ошибки замкнутой импульсной САУ (относительно сигнала y(t). 7. Провести сравнение расчетных результатов с данными, полученными моделированием в Matlab (Simulink).
Таблица 2
Литература 1. Теория автоматического управления. / Под ред. А.В.Нетушила. М.: Высшая школа 1982. 400с. 2. Теория автоматического управления. / Под ред. А.А.Воронова. М.: Высшая школа 1986. 504с.
3. Исследование САУ с использованием прикладного пакета MATLAB. Лабораторный практикум по курсу “Основы автоматического управления”, Т.В.Ягодкина, С.А.Хризолитова, В.М.Беседин, М.: Изд-во МЭИ, 2007. - 89 с 4.. Основы теории импульсных и цифровых систем. Учебное пособие, Коломейцева М.Б., Беседин В.М., Ягодкина Т.В., Издательский Дом МЭИ, 2007. 106 с. 5. Применение Mathcad для решения задач теории автоматического управления. Учебное пособие по курсу «Основы теории управления», Т.В. Ягодкина, С.А. Хризолитова, О.А. Бондин, М.:Изд-во МЭИ, 2004. – 52 с. [1] Если импульсная САУ при заданном коэффициенте усиления окажется неустойчивой, то построение переходного процесса и определение статической и кинетической ошибок следует осуществить для системы с коэффициентом усиления, как минимум, в 1,5¸2 раза меньше предельного. [2] Удобнее эти преобразования делать в Mathcad
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.179.120 (0.01 с.) |

 ):
):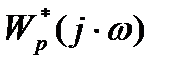 охватывает точку с координатами (-1,j0), а разомкнутая импульсная САУ находится на границе устойчивости, то рассматриваемая САУ в замкнутом состоянии является неустойчивой.
охватывает точку с координатами (-1,j0), а разомкнутая импульсная САУ находится на границе устойчивости, то рассматриваемая САУ в замкнутом состоянии является неустойчивой.
 – коэффициент усиления разомкнутой САУ;
– коэффициент усиления разомкнутой САУ; 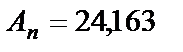 – модуль комплексного коэффициента усиления при его аргументе равном -1800.
– модуль комплексного коэффициента усиления при его аргументе равном -1800.
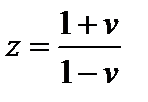 . Тогда характеристическое уравнение
. Тогда характеристическое уравнение 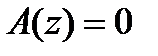 принимает вид:
принимает вид:

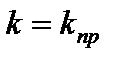 представим следующим образом:
представим следующим образом: .
. примет вид:
примет вид:
 ,
, 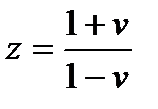 . Тогда, после преобразований, получим:
. Тогда, после преобразований, получим:
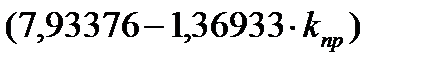 ; a1=
; a1= 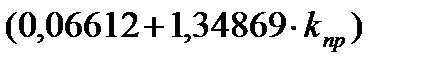 ;
; ; a3=
; a3=  , которое выполняется,
, которое выполняется,
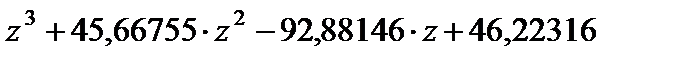 .
. и для этого коэффициента усиления разомкнутой системы определим устойчивость замкнутой системы на основе корней характеристического уравнения.
и для этого коэффициента усиления разомкнутой системы определим устойчивость замкнутой системы на основе корней характеристического уравнения. получим, что:
получим, что: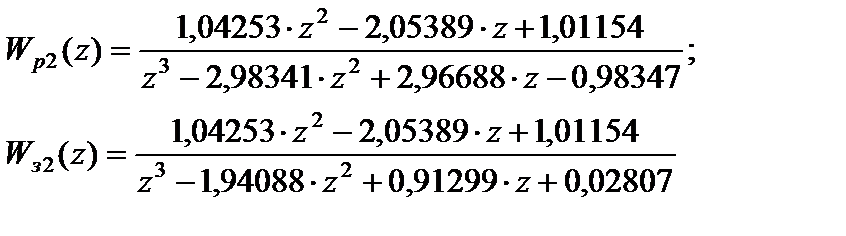
 , т.е.
, т.е.  – значит, замкнутая САУ является устойчивой.
– значит, замкнутая САУ является устойчивой.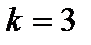 .
.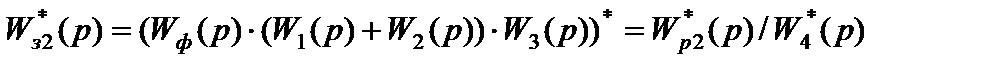 =
=
 на
на 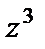 . Тогда
. Тогда
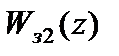 :
:

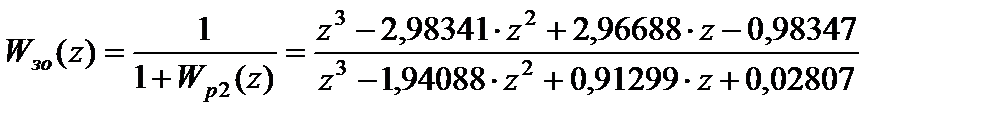
 :
:
 или
или 




 ;
; найти дискретную передаточную функцию разомкнутой импульсной системы
найти дискретную передаточную функцию разомкнутой импульсной системы  ;
; ;
;