
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды отбора единиц в выборочную совокупностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В зависимости от способа выборки единиц из генеральной совокупности различают следующие виды отбора (выборки): собственно случайный, механический, типический (районированный, стратифицированный), серийный (гнездовой), комбинированный, многофазный и др.
При собственно случайном отборе единицы отбираются из генеральной совокупности в строгом соответствии с научными принципами и правилами случайного отбора. Прежде чем производить собственно случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку. Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно. Так, если пользоваться таблицами случайных чисел, то нужно перенумеровать все единицы генеральной совокупности, а если жеребьевкой, то на каждую единицу необходимо заготовить соответствующие карточки или фишки. При проведении многих выборочных обследований генеральная совокупность оказывается настолько большой, что проводить такую предварительную работу практически невозможно и нецелесообразно. Поэтому для удобства проведения выборочного наблюдения на практике применяют другие формы отбора, организуемые таким образом, чтобы была обеспечена случайность выборки.
Механический отбор применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.д.). При механическом отборе генеральная совокупность делится на n равных частей в соответствии с естественным расположением ее границ (географическим, пространственным, алфавитным и др.) и из каждой части обследуется одна единица. (В соответствии с требуемым объемом выборки с шагом Например, если нужно отобрать 10% рабочих, то обследуют каждого десятого рабочего по списку, упорядоченного по алфавиту. Ошибки репрезентативности при механическом отборе возникают не в результате случайности отбора, а в результате случайности размещения единиц изучаемой совокупности. Списки единиц совокупности должны быть составлены так, чтобы упорядочение единиц совокупности не было связано с изучаемыми свойствами.
Если единицы в генеральной совокупности размещены случайно в отношении изучаемого признака (в алфавитном порядке, в порядке времени поступления единиц совокупности), то ошибка механической выборки становится случайной и ее можно определять по формуле ошибки случайной выборки. Механический отбор удобно проводить, когда уже имеются списки единиц совокупности и когда имеют дело с генеральной совокупностью, численность которой известна лишь приблизительно и единицы которой появляются постепенно, например, при контроле качества услуг. Средняя ошибка выборки при механическом отборе определяется по формуле средней ошибки выборки для собственно-случайного отбора. Следовательно, объем выборки определяется также, как и для собственно случайного отбора.
Типический (районированный, стратифицированный) отбор осуществляется на основе предварительного разделения единиц генеральной совокупности на типические группы (районы, страты) по изучаемым признакам. В качестве групп, страт в зависимости от характера изучаемого признака могут использоваться: для обследования предприятий - округа, регионы, отрасли, формы собственности предприятия; для населения – регионы, социальные, возрастные группы. Типическая выборка применяется в случае когда генеральная совокупность неоднородна и это влияет на размер изучаемого признака. Тогда применяют предварительное деление генеральной совокупности на типические однородные группы. Отбор из каждой группы может осуществляться в случайном (повторном или бесповторном) или механическом порядке. Объем выборки в каждой типической группе обычно устанавливается пропорционально ее удельному весу в генеральной совокупности (пропорциональный отбор). Это повышает точность выборочного наблюдения, поскольку более точно, чем при собственно случайной выборке, отражается структура генеральной совокупности.
где
При различиях в однородности типических групп лучшие результаты дает распределение запланированного объема выборки между типическими группами не только с учетом их объема, но и с учетом дисперсии признака (оптимальный отбор).
Такой отбор дает лучшие результаты, однако на практике его применение затруднительно вследствие трудности получения сведений о вариации до проведения обследования. При типической выборке устраняется влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как имеется представительство в выборочной совокупности каждой из типических групп. Средняя ошибка выборки здесь зависит не от общей дисперсии s2, а от средней из групповых дисперсий Следовательно, для того, чтобы типическая выборка была наиболее эффективной, нужно сформировать группы таким образом, чтобы удельный вес межгрупповой дисперсии в общей дисперсии был как можно больше. При определении ошибки типической выборки в случае пропорционального отбора применяется формула случайной выборки, в которой вместо дисперсии s2 применяется средняя из групповых дисперсий
где ni – численность единиц выборочной совокупности i-й группы; s2i – выборочная дисперсия i-й группы. Объем выборки определяется:
Цель типической выборки: o обеспечение представительства в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам, o повышение точности результатов выборочного наблюдения.
В статистике находит применение серийный (гнездовой) отбор, при котором в случайном порядке отбираются не единицы, а группы единиц (серии, гнезда). Серии, или группы, единиц отбираются по принципу случайного отбора или механическим способом, внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серии состоят из единиц, связанных между собой различным образом: o территориально (районы, поселки), o организационно (предприятия, цеха, бригады), o во времени (совокупность единиц продукции, произведенной за конкретный отрезок времени). Серийный отбор удобен в тех случаях, когда единицы совокупности естественным образом объединены в группы (серии). Например, в качестве серий могут рассматриваться партии товара, бригады и т.д. Если общее число серий в генеральной совокупности обозначить через R, а число отобранных серий – r, то средняя ошибка выборки может быть определена по формуле mx = где s2x – межсерийная (межгрупповая) дисперсия. Чем меньше серийные средние отличаются одна от другой, т.е. чем ближе друг к другу серии по уровню изучаемого признака, тем точнее серийная выборка. Объем серийной выборки определяется
На практике в зависимости от цели и задач выборочного обследования часто выборки производят на основе сочетания двух и более способов, образующих ступени отбора: механический и серийный, типический и механический, серийный и собственно случайный. Такие выборки получили название комбинированных (ступенчатых, многоступенчатых). На каждой ступени используются разные единицы отбора: более крупные на начальных ступенях, на последней ступени единица отбора совпадает с единицей наблюдения. При комбинированном отборе общая ошибка выборки состоит из ошибок на каждой ее ступени. К многоступенчатым выборкам обращаются при проведении крупных выборочных обследований для получения достаточной репрезентативности с наименьшими затратами на их организацию и проведение.
Средняя ошибка выборки при двухступенчатом отборе рассчитывается по формуле:
Еще один вид выборочного наблюдения – многофазная выборка. Такая выборка включает определенное количество фаз, каждая из которых отличается подробностью программы наблюдения. Например, 25% всей генеральной совокупности обследуются по краткой программе, каждая четвертая единица из этой выборки обследуется по более полной программе. Многофазная выборка характеризуется тем, что так же, как и многоступенчатая выборка, включает несколько стадий отбора, но в отличие от последней на всех ее ступенях сохраняется одна и та же единица отбора. Каждая ступень отбора имеет свой объем выборки и свою программу наблюдения.
Малая выборка В процессе оценки степени представительности данных выборочного наблюдения важное значение приобретает вопрос об объеме выборочной совокупности Но уже при В выборках небольшого объема Малой называют выборку, объем которой находится в пределах 5...30 ед. Особенностью малой выборки является то, что ее случайные ошибки не подчиняются закону нормального распределения, а имеют особый закон распределения. Поэтому при оценке результатов малой выборки нельзя пользоваться формулами собственно случайного отбора.
Результаты малой выборки оцениваются по закону распределения вероятностей Стьюдента. Английский математик Стьюдент доказал, что вероятность того, что | является функцией от t* и n, где n – численность выборки, t* – отношение Стьюдента. В 1908 г. им было построено специальное распределение, которое позволяет и при малых выборках соотносить Плотность вероятностей распределения Стьюдента описывается функцией
При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента, определяемым по формуле
где Величина
Данная величина используется лишь для исследуемой совокупности, а не в качестве приближенной оценки Распределение Стьюдента имеет параметр «число степеней свободы» -
При небольшой численности выборки распределение Стьюдента отличается от нормального: большие величины критерия имеют здесь большую вероятность, чем при нормальном распределении. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. На практике пользуются таблицами распределения Стьюдента S(t*), в которых для различных n и t* приведены вероятности Р(t*). В табл. 10.1 даны значения доверительной вероятности Р(t*), рассчитанные для различных t* и k (k – число степеней свободы, равное n–1).
Таблица 10.1. Доверительная вероятность Р(t*)
По этой таблице определяется двусторонний критерий, т.е. вероятность того, что фактическое значение t* по случайным причинам не будет больше табличного по абсолютной величине. Средняя ошибка малой выборки рассчитывается по формуле mмв = Предельная ошибка малой выборки равна Dмв=t*∙m мв.
Моментные наблюдения Одним из вариантов выборочного метода для изучения использования рабочего времени и времени работы оборудования является метод моментных наблюдений. Этот метод состоит в регистрации вида затрат времени в определенные, заранее выбранные моменты. Предварительно составляется список всех возможных состояний или видов затрат времени. Так как статистическая отчетность такой информации не содержит, то моментные наблюдения являются единственным ее источником. Метод заключается в том, что в заранее выбранные моменты фиксируется состояние процесса (например, работа – простой). Его особенность состоит в том, что по охвату объекта совокупности метод является сплошным, а по времени – выборочным. Интервалы времени между моментами наблюдения могут быть равными и неравными. Продолжительность интервала и число моментов наблюдения определяются в соответствии с теорией выборочного метода. Моменты наблюдения могут отбираться по таблицам случайных чисел или периодически через определенные промежутки времени по способу механического отбора.
Необходимая численность моментов наблюдения определяется как
В силу необратимости времени отбор моментов в выборочную совокупность всегда является бесповторным. Но поскольку общее количество существующих моментов времени (генеральная совокупность) очень большое, в моментном наблюдении используют формулы ошибок повторного отбора. Средняя ошибка моментных наблюдений рассчитывается по формуле
где w – коэффициент потерь рабочего времени, доля простоев оборудования во всем рабочем времени.
СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.253.84 (0.012 с.) |

 ).
). ,
, - численность i-й группы в генеральной совокупности,
- численность i-й группы в генеральной совокупности, - объем выборки из i-й группы.
- объем выборки из i-й группы. ,
, - дисперсия признака в i-й группе генеральной совокупности.
- дисперсия признака в i-й группе генеральной совокупности.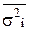 . Так как средняя из групповых дисперсий всегда меньше общей дисперсии, при прочих равных условиях ошибка типической выборки меньше ошибки собственно случайного отбора.
. Так как средняя из групповых дисперсий всегда меньше общей дисперсии, при прочих равных условиях ошибка типической выборки меньше ошибки собственно случайного отбора. ;
;  ,
,
 ,
, 
 ,
,
 ,
, 
 ,
,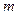 - число отобранных «крупных» единиц,
- число отобранных «крупных» единиц, - дисперсия признака х по совокупности «крупных» единиц,
- дисперсия признака х по совокупности «крупных» единиц, - дисперсия признака х в каждой из отобранных «крупных» единиц,
- дисперсия признака х в каждой из отобранных «крупных» единиц, . При большом числе единиц выборочной совокупности (
. При большом числе единиц выборочной совокупности ( ) распределение случайных ошибок выборочной средней нормально или приближается к нормальному по мере увеличения числа наблюдений. Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа.
) распределение случайных ошибок выборочной средней нормально или приближается к нормальному по мере увеличения числа наблюдений. Вероятность выхода ошибки за определенные пределы оценивается на основе таблиц интеграла Лапласа. возникает несоответствие между табличными значениями и вероятностью предела; при
возникает несоответствие между табличными значениями и вероятностью предела; при  погрешность становится значительной. Несоответствие обусловлено характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, т.к. распределение ошибок выборки при большой выборке всегда оказывается нормальным.
погрешность становится значительной. Несоответствие обусловлено характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, т.к. распределение ошибок выборки при большой выборке всегда оказывается нормальным. |<t*m,
|<t*m, и доверительную вероятность
и доверительную вероятность  . При
. При  различия незначительны. Поэтому приактически к малым выборкам относят выборки объемом менее 30 единиц.
различия незначительны. Поэтому приактически к малым выборкам относят выборки объемом менее 30 единиц. ,
, - текущая переменная (критерий Стьюдента),
- текущая переменная (критерий Стьюдента),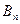 - величина, зависящая лишь от
- величина, зависящая лишь от  ,
, - мера случайных колебаний выборочной средней в малой выборке.
- мера случайных колебаний выборочной средней в малой выборке. вычисляется на основе данных выборочного наблюдения:
вычисляется на основе данных выборочного наблюдения:

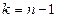
 или
или  .
. .
.



