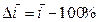Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные показатели рядов динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Абсолютный прирост (абсолютное изменение) уровней определяется как разность между двумя уровнями ряда. Он показывает, на сколько (в единицах измерения показателей ряда) уровень одного периода больше или меньше уровня какого-либо предшествующего периода. В зависимости от базы сравнения абсолютные приросты делятся на цепные и базисные: цепные где yi уровень i-го члена ряда; yi-1 – уровень предшествующего i-му члена ряда; y1 – уровень начального (базисного) члена ряда. Если уровни ряда динамики не возрастают, а уменьшаются, то абсолютную разность уровней показывают со знаком "–". В этом случае говорят не об абсолютном приросте, а об абсолютном уменьшении размера явления. Если значения цепных абсолютных приростов (изменений) постоянны, то уровни ряда изменяются равномерно. Если же абсолютные приросты от периода к периоду возрастают (или убывают), то уровни изменяются ускоренно (или замедленно). В этом случае можно рассчитать показатель ускорения как разность между двумя смежными цепными абсолютными приростами:
Темп роста представляет собой отношение одного уровня ряда к другому и показывает, во сколько раз один уровень больше другого. Если все уровни ряда сопоставить с уровнем одного какого-либо периода, принятого за базу сравнения (обычно начального), то получается ряд базисных темпов роста, если сопоставление производится по отношению к уровню предыдущего периода, то образуется ряд цепных темпов роста:
где yi уровень i-го члена ряда; yi-1 – уровень предшествующего i-му члена ряда; y1 – уровень начального (базисного) члена ряда. Темпы роста выражаются: в коэффициентах, если основание сравнения принимается за единицу, в процентах, если основание сравнения принимается за 100. Выраженные в коэффициентах темпы роста показывают, во сколько раз уровень данного периода больше уровня базы сравнения или какую часть он составляет. При процентном выражении темп роста показывает, сколько процентов составляет уровень данного периода от уровня базы сравнения.
Между базисными и цепными темпами роста существует взаимосвязь: произведение цепных темпов равно базисному, частное от деления базисных темпов равно промежуточному цепному темпу. Представим произведение трех цепных индексов: I2/1I3/2I4/3 = Из записи видно, что промежуточные уровни сокращаются и в результате получается отношение конечного уровня к начальному, т.е. базисный темп роста. Теперь разделим два базисных темпа роста, например, за четвертый и третий периоды: I4/1: I3/1 = Получен цепной темп роста.
Относительную оценку абсолютного прироста дают показатели темпа прироста. Темпы прироста делятся на цепные и базисные, исчисляются делением абсолютного прироста на предыдущий (или первоначальный) уровень и выражаются в процентах: цепные Темп прироста показывает, на сколько процентов данный уровень больше (или меньше) другого уровня, принятого за базу сравнения. Темпы прироста могут быть отрицательными. В этом случае они указывают, на сколько процентов уменьшились размеры явления. Темп прироста можно получить непосредственно из темпа роста. Для этого следует из темпа роста, выраженного в процентах, вычесть 100; DI=I–100. Абсолютное значение одного процента прироста - отношение абсолютного прироста уровня к темпу прироста (в процентах) за соответствующий период:
Для базисных абсолютных приростов и темпов прироста расчет
Средний уровень ряда дает общую характеристику показателя за весь период, охватываемый рядом динамики. Средний уровень в интервальном и моментном рядах динамики определяется по-разному. В интервальном динамическом ряду с равными интервалами средний уровень рассчитывается по формуле простой средней арифметической
В моментном ряду динамики средний уровень определяется: С равными промежутками времени между моментами: по средней хронологической
где n – число уровней ряда динамики; y1, y2,..., yn – первый, второй,..., n-й члены моментного ряда динамики. По приведенной формуле средний уровень может быть исчислен только для такого ряда, в котором все члены равно отстоят друг от друга, например, если все данные приведены на начало каждого месяца, квартала или года. В случае неравных промежутков между моментами средний уровень ряда определяется: 1) если в промежутках между моментами уровни
Т.к. в промежутках между моментами уровни принимают разные значения, мы их 2-х известных уровней определяем средние, из которых мы определяем среднюю для всего анализируемого периода. 2) в промежутках между моментами каждое значение Тогда средний уровень определяется по средней арифметической взвешенной, в качестве весов в которой принимается время между значениями моментов
где t – количество дней (месяцев, лет), в течение которых сохранялось данное значение уровня ряда. Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели. Средний абсолютный прирост (изменение) уровней определяется как средняя арифметическая простая из отдельных цепных приростов
где
Чтобы охарактеризовать интенсивность развития явления за длительный период, определяют средний темп роста. Средний темп роста служит сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики и показывает во сколько раз в среднем за единицу времени изменился уровень динамического ряда. Средний темп роста определяется по формуле средней геометрической из цепных темпов роста
где I1, I2, I3,..., Im – цепные темпы роста, выраженные в коэффициентах; m – количество цепных темпов роста; m = n–1 (n – число уровней ряда динамики). Необходимость исчисления среднего темпа роста за весь период возникает вследствие колеблемости темпов роста по отдельным периодам. Средний темп роста рассчитывается не по средней арифметической, в которой объем варьирующего признака определяется суммой значений, а по средней геометрической, в которой объемом варьирующего признака является темп роста за весь анализируемый период (за все годы), который находят уже не суммированием, а как произведение цепных (ежегодных) темпов роста.
Средний же темп роста определяется после извлечения корня из произведения цепных темпов роста, степень которого равна количеству цепных темпов. Расчет среднегодовых темпов роста может быть выполнен также непосредственно по абсолютным данным исходного ряда динамики:
Для расчета среднегодового темпа роста нужно знать значения начального и конечного уровней ряда и количество лет в анализируемом периоде. В этом случае формула расчета среднего темпа роста примет вид
где yn – конечный уровень ряда; y1 – начальный уровень ряда; n – число уровней динамики. Необходимо обратить внимание, что в данной формуле число абсолютных уровней ряда динамики на единицу больше показателя степени корня. Средние темпы прироста определяются на основе средних темпов роста путем вычитания из последних 100%
Все рассмотренные аналитические показатели рядов динамики – уровни, темпы роста и прироста, абсолютные и относительные приросты – при анализе интенсивности развития явления применяются комплексно, совместно. Только в этом случае можно правильно и полно охарактеризовать изучаемое явление.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.222 (0.011 с.) |

 , базисные
, базисные 

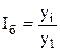 ;
; 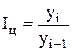 ,
, = I4/1.
= I4/1. = I4/3.
= I4/3. , базисные
, базисные  .
.
 .
. смысла не имеет.
смысла не имеет. .
. ,
, принимают разные значения
принимают разные значения
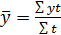 ,
,
 - число уровней ряда,
- число уровней ряда,
 ,
, ,
, 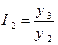 , …
, … 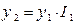 ,
, 
 .
.