
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 11. Обыкновенные дифференциальные уравненияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Раздел 11. Обыкновенные дифференциальные уравнения 1. Физические задачи, приводящие к дифференциальным уравнениям. ОДУ 1-го порядка: определение, формы записи. Задача Коши, теорема существования и единственности решения задачи Коши. Изоклины. Основные классы ОДУ 1-го порядка, интегрируемые в квадратурах Физические задачи, приводящие к дифференциальным уравнениям Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков. В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки. Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
Тогда получаем: Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида F (x, y, y ')=0, где F — известная функция трех переменных, определенная в области G из R 3, x — независимая переменная из интервала (a, b), y (x) — неизвестная функция, y '(x) — ее производная. Обыкновенные дифференциальные уравнения, разрешенные относительно производной, т.е. уравнения вида y '= f (x, y) называют уравнениями в нормальной форме. P(x,y)dx+Q(x,y)dy=0 – дифференциальная форма ЗадачаКоши: Задача отыскивания решения ДУ первого порядка P(x,y)dx+Q(x,y)dy=0, удовлетворяющего заданному условию Теорема существования и единственности решения задачи Коши. Если в некоторой окрестности точки (х0,у0) функция f(х,у) определена, непрерывна и имеет непрерывную частную производную f¢y, то существует такая окрестность точки (х0,у0), в которой задача Коши имеет решение, притом единственное. (приводится без доказательства)
Изоклины Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f (x, y), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. С помощью изоклин можно приближённо изобразить интегральные кривые.
Общая теория ЛОДУ и ЛНДУ. Определитель Вронского. Формула Остроградского-Лиувилля. Основная теорема о структуре общего решения ЛОДУ (ЛНДУ).
Определитель Вронского. Определение. Если из функций yi составить определитель n – го порядка
то этот определитель называется определителем Вронского. (Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик) Теорема. Если функции Теорема. Если функции Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема. Если
где Ci – постоянные коэффициенты. Формула Лиувилля-Остроградского устанавливает связь между вронскианом W (x), построенном на базе частных решений y 1(x), y 2(x), и коэффициентом a 1(x) в дифференциальном уравнении. Пусть W (x) − определитель Вронского решений y 1(x), y 2(x) линейного однородного дифференциального уравнения 2-го порядка
в котором функции a 1(x) и a 2(x) непрерывны на отрезке [ a,b ]. Пусть точка x 0 принадлежит отрезку [ a,b ]. Тогда для всех
Теорема 2 (о структуре общего решения неоднородного дифференциального уравнения). Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения:
где y (n) + a 1 y (n -1) +... +any = 0, Докажем теорему для уравнения второго порядка y // + py / + qy = f (x). (4) где p, q – константы, f (x) Рассмотрим соответствующее однородное ДУ: y // + py / + q = 0. (5) Обозначим y 1, y 2 его линейно независимые частные решения и y 0 = c 1 y 1 + c 2 y 2 – его общее решение.) Пусть
Перегруппируем:
Получаем тождественное равенство, так как первая скобка обращается в нуль в силу того, что y 0– общее решение однородного ДУ(5), а вторая скобка равна правой части, так как Теперь надо решить вопрос: как же найти частное решение ДУ (1). Теорема 1 (о структуре общего решения линейного однородного ДУ). Если функции y 1(x), y 2(x), …, y n (x) образуют фундаментальную систему решений ДУ (2), то функция
является общим решением этого уравнения в области
ci – произвольные постоянные, [ а, b ] – область непрерывности коэффициентов ai (x) уравнения (2), i = 1,2,..., n.
5. ЛОДУ и ЛНДУ с постоянными коэффициентами. ЛНДУ с правой частью специального вида. Метод вариации произвольных постоянных. Раздел 11. Обыкновенные дифференциальные уравнения 1. Физические задачи, приводящие к дифференциальным уравнениям. ОДУ 1-го порядка: определение, формы записи. Задача Коши, теорема существования и единственности решения задачи Коши. Изоклины. Основные классы ОДУ 1-го порядка, интегрируемые в квадратурах
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.111.44 (0.006 с.) |


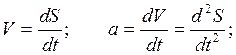
 - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
- уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t). называется задачей Коши.
называется задачей Коши.  ,
, линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю. ,
,
 справедлива формула Лиувилля-Остроградского:
справедлива формула Лиувилля-Остроградского:
 , (3)
, (3) – частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2):
– частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2): 0.
0. .
.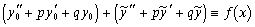 .
. (3)
(3) ,
,  ,
,  , …,
, …,  ;
;


