
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая теория лоду и лнду. Определитель Вронского. Формула остроградского-лиувилля. Основная теорема о структуре общего решения лоду (лнду).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определитель Вронского. Определение. Если из функций yi составить определитель n – го порядка
то этот определитель называется определителем Вронского. (Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик) Теорема. Если функции Теорема. Если функции Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения Теорема. Если
где Ci – постоянные коэффициенты. Формула Лиувилля-Остроградского устанавливает связь между вронскианом W (x), построенном на базе частных решений y 1(x), y 2(x), и коэффициентом a 1(x) в дифференциальном уравнении. Пусть W (x) − определитель Вронского решений y 1(x), y 2(x) линейного однородного дифференциального уравнения 2-го порядка
в котором функции a 1(x) и a 2(x) непрерывны на отрезке [ a,b ]. Пусть точка x 0 принадлежит отрезку [ a,b ]. Тогда для всех
Теорема 2 (о структуре общего решения неоднородного дифференциального уравнения). Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения:
где y (n) + a 1 y (n -1) +... +any = 0, Докажем теорему для уравнения второго порядка y // + py / + qy = f (x). (4) где p, q – константы, f (x) Рассмотрим соответствующее однородное ДУ: y // + py / + q = 0. (5) Обозначим y 1, y 2 его линейно независимые частные решения и y 0 = c 1 y 1 + c 2 y 2 – его общее решение.) Пусть
Перегруппируем:
Получаем тождественное равенство, так как первая скобка обращается в нуль в силу того, что y 0– общее решение однородного ДУ(5), а вторая скобка равна правой части, так как Теперь надо решить вопрос: как же найти частное решение ДУ (1). Теорема 1 (о структуре общего решения линейного однородного ДУ). Если функции y 1(x), y 2(x), …, y n (x) образуют фундаментальную систему решений ДУ (2), то функция
является общим решением этого уравнения в области
ci – произвольные постоянные, [ а, b ] – область непрерывности коэффициентов ai (x) уравнения (2), i = 1,2,..., n.
5. ЛОДУ и ЛНДУ с постоянными коэффициентами. ЛНДУ с правой частью специального вида. Метод вариации произвольных постоянных.
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
, линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю. ,
,
 справедлива формула Лиувилля-Остроградского:
справедлива формула Лиувилля-Остроградского:
 , (3)
, (3) – частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2):
– частное решение ДУ(1), y 0 – общее решение соответствующего однородного ДУ (2): 0.
0. .
.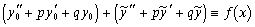 .
. (3)
(3) ,
,  ,
,  , …,
, …,  ;
;


