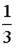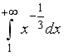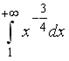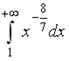Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
V2: Приложения дифференциального исчисления ФОП.Содержание книги
Поиск на нашем сайте
I: S: Функция -: 0 +: 4 -: Ни при каком х -: 2 I: S: Функция -: 0 -: 4 -: 2 +: Ни при каком х I: S: Функция +: 1 -: 5 -: Ни при каком х -: 3 I: S: Функция -: Ни при каком х -: -4 +: 0 -: 4 I: S: Функция +: Ни при каком х -: -2 -: 4 -: 0 I: S: Функция -: 1 +: 5 -: Ни при каком х -: 3 I: S: Функция -: Ни при каком х -: -4 +: 0 -: 4 I: S: Функция -: Ни при каком х +: -3 -: 3 -: 1 I: S: График функции +: -: -: -: I: S: Функция -: +: -: I: S: Функция -: +: -: I: S: Функция -: +: -: I: S: Функция +: -: -: I: S: Функция -: +: -: I: S: Функция +: -: -: I: S: Функция +: -: -: I: S: Функция +: -: -: I: S: Функция -: +: -: I: S: Функция -: +: -: I: S: Функция, график которой представлен на рисунке,
имеет … точек перегиба. +: 2 I: S: Функция, график которой представлен на рисунке,
имеет … точек перегиба. +: 3 V1: Дифференциальное исчисление функций нескольких переменных V2: Частные производные первого порядка. I: S: Частная производная -: -: -: +: I: S: Частная производная +: -: -: -: I: S: Частная производная -: +: -: -: I: S: Частная производная -: -: -: +: I: S: Частная производная -: -: -: +: I: S: Частная производная -: -: +: -: I: S: Частная производная -: +: -: -: I: S: Частная производная +: -: -: -: V2: Частные производные высших порядков I: S: Смешанная производная второго порядка функции +: -: -: -: I: S: Частная производная второго порядка по переменной -: -: -: +: I: S: Частная производная второго порядка по переменной
-: -: +: -: I: S: Смешанная производная второго порядка функции +: -: -: -: I: S: Частная производная второго порядка по переменной -: +: -: -: I: S: Частная производная второго порядка по переменной -: -: +: -: I: S: Смешанная производная второго порядка функции +: -: -: -: I: S: Частная производная второго порядка по переменной -: +: -: -: I: S: Частная производная второго порядка по переменной -: -: +: -: V1: Интегральное исчисление V2: Неопределенный интеграл I: S: Множество первообразных функции -: +: -: -: I: S: Первообразными функции +: -: +: -: +: I: S: Первообразными функции -: +: +: -: I: S: Первообразными функции -: +: +: -: I: S: Первообразными функции -: +: +: -: I: S: Первообразными функции -: +: -: +: I: S: Первообразными функции +: -: -: +: I: S: Первообразными функции -: +: +: -: I: S: Первообразными функции +: -: +: -: I: S: Первообразными функции +: +: -: -: I: S: Первообразными функции +: +: -: -: V2: Определенный интеграл I: S: Среднее значение функции -: -: 1 +: -: I: S: Среднее значение функции -: -: 1 +: -: I: S: Среднее значение функции -: +: 0 -: -: I: S: Среднее значение функции -: -: 1 -: +: 0 I: S: Среднее значение функции -: -: 0 +: -: I: S: Определенный интеграл +: – 0.5 -: 0.5 -: 0 -: – 2 I: S: Определенный интеграл -: +: -: -: I: S: Определенный интеграл -: +: -: -: I: S: Объем тела, образованного вращением вокруг оси -: +: -: -: I: S: Объем тела, образованного вращением вокруг оси -: -: -: +: I: S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как … -: +: -: -: I: S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как … -: -: +: -: I: S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как … -: -: -: +: I: S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как … -: -: -: +: I: S: Площадь фигуры, ограниченной линиями -: -: -: +: I: S: Площадь фигуры, ограниченной линиями -: +: -: -: V2: Несобственные интегралы I: S: Несобственный интеграл обозначается: -: +: +: -: +: I: S: Несобственным интегралом называется: -: +: +: -: I: S: Несобственный интеграл +: 0.5 -: -: -0.5 -: 4 I: S: Несобственный интеграл +: 0.25 -: - 0.25 -: -: 8 I: S: Несобственный интеграл -: 4 -: +: -: I: S: Сходящимися являются несобственные интегралы … -: +: -: +: I: S: Сходящимися являются несобственные интегралы … -: +: -: +: I: S: Сходящимися являются несобственные интегралы … -: -: +: +: I: S: Сходящимися являются несобственные интегралы … +: -: -: +: I: S: Сходящимися являются несобственные интегралы … -: -: +: +:
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.154.143 (0.01 с.) |

 имеет минимум при x =...
имеет минимум при x =... имеет минимум при x =...
имеет минимум при x =... имеет максимум при x =...
имеет максимум при x =... имеет максимум при x =...
имеет максимум при x =... имеет минимум при x =...
имеет минимум при x =... имеет минимум при x =...
имеет минимум при x =...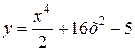 имеет минимум при x =...
имеет минимум при x =... имеет максимум при x =...
имеет максимум при x =... обращен выпуклостью вверх на промежутке …
обращен выпуклостью вверх на промежутке …



 является вогнутой на интервале …
является вогнутой на интервале …


 является вогнутой на интервале …
является вогнутой на интервале … является вогнутой на интервале …
является вогнутой на интервале …

 является вогнутой на интервале …
является вогнутой на интервале …


 является вогнутой на интервале …
является вогнутой на интервале … является вогнутой на интервале …
является вогнутой на интервале …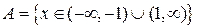


 является вогнутой на интервале …
является вогнутой на интервале …


 является вогнутой на интервале …
является вогнутой на интервале …


 является вогнутой на интервале …
является вогнутой на интервале …


 является вогнутой на интервале …
является вогнутой на интервале …

 функции
функции 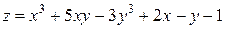 равна …
равна …



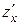 функции
функции  функции
функции  равна …
равна …



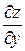 функции
функции  равна …
равна …



 равна …
равна …



 равна …
равна …



 функции
функции  функции
функции  равна …
равна …



 равна …
равна …

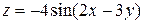
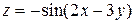
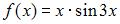 описывается соотношением …
описывается соотношением …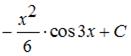

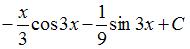

 являются …
являются …




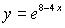 являются…
являются…



 являются…
являются…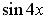



 являются…
являются…

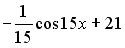

 являются…
являются…


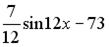
 являются…
являются…



 являются…
являются…



 являются…
являются…



 являются…
являются…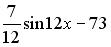

 являются…
являются…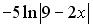



 на отрезке
на отрезке  равно …
равно …
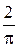

 на отрезке
на отрезке  равно …
равно …

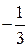
 равно …
равно … на отрезке
на отрезке  равно …
равно …

 равно …
равно …
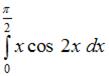 равен …
равен … равен…
равен…
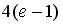


 равен…
равен…
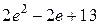


 фигуры, ограниченной параболой
фигуры, ограниченной параболой  и осью
и осью 
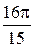

 , равен …
, равен …





















 ,
, 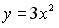 ,
,  , вычисляется с помощью определенного интеграла…
, вычисляется с помощью определенного интеграла…



 ,
, 









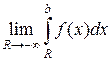

 равен …
равен …
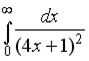 равен …
равен … равен …
равен …