
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фдз 1. Матрицы. Операции над матрицами.Содержание книги
Поиск на нашем сайте
Фдз 1. Матрицы. Операции над матрицами. Операции с матрицами: равенство матриц; умножение матрицы на число; сложение матриц; перемножение матриц. Транспонирование матрицы. Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица. Возведение квадратной матрицы в натуральную степень.
1. Для матриц
2. Для матриц
3. (в случае невыполнимости операции указать причину невыполнимости):
4.
Какие из приведенных выше матриц являются: 1) симметрическими; 2) диагональными; 3) треугольными; 4) единичными. ________________________________________________________________________
Домашнее задание. 1. Для заданных матриц найти
Фдз 2. Определители. Определитель Основные свойства определителей.
1. Установить четность (нечетность) перестановок: 2. Дать определение определителя 3. Записать правила Саррюса вычисления определителей 1-го, 2-го, 3-го порядков. 4. Вычислить по правилам Саррюса определители:
5. Сформулировать основные свойства определителей. 6. Почему можно не вычисляя указанных ниже определителей сразу сказать, что каждый из них равен нулю?
7. Вычислить определители: 8. Вычислить следующие определителя, сведя их к определителям треугольных матриц:
___________________________________________________________________________ Домашнее задание. 1. Определить четность перестановки 2. Даны квадратные матрицы
1) Вычислить определители матриц 2) Вычислить определитель матрицы
Фдз 3. Определители (продолжение). Обратная матрица Миноры и алгебраические дополнения. Разложение определителя по строке (столбцу). Обратная матрица, ее нахождение.
1. Сформулировать теорему о разложении определителя по строке (столбцу). 2. Найти миноры по правилу Саррюса; разложением по 2-й строке; разложением по 1-му столбцу. 3. Найти миноры по правилу Саррюса; разложением по 3-й строке; разложением по 2-му столбцу.
4. Вычислить определитель разложением по 2-й строке; разложением по 3-му столбцу. 5. Дать определение обратной матрицы. 6. Найти обратные матрицы для матриц (если это невозможно, указать причину):
Выполнить проверку найденных обратных матриц.
_________________________________________________________________________
Домашнее задание. 1. Дана матрица Найти миноры Вычислить определитель матрицы а) разложением по 3-й строке; б) разложением по 4-му столбцу.
2. Найти обратные матрицы для матриц
Фдз 4. Использование матриц и определителей при решении линейных алгебраических систем. Совместные, несовместные линейные системы. Матричная запись линейной системы. Невырожденные линейные системы. Решение невырожденных систем по правилу Крамера и с помощью обратной матрицы.
1. Даны три системы уравнений:
Какие из этих систем являются линейными системами? 2. Какие линейные системы называются совместными (несовместными)? Привести примеры совместной и несовместной линейных систем. 3. Сформулировать правило Крамера. 4. Даны три линейные системы:
Выявить из данных систем те, которые можно решить с помощью правила Крамера и решить их с помощью этого правила. 5. Записать системы из задания 4. в матричном виде. 6. В каком случае матричные уравнения 7. Выделить из систем задания 4. системы, которые можно решить матричным методом и решить их этим методом.
____________________________________________________________________________
Домашнее задание. 1. Решить систему а) с помощью правила Крамера; б) с помощью обратной матрицы.
2. Решить следующие матричные уравнения:
Фдз 8. Прямая на плоскости. Различные виды задания прямой на плоскости. Основные задачи по нахождению прямой на плоскости. Взаимное расположение двух прямых. Угол между прямыми. Расстояние от точки до прямой.
1. Записать общее, каноническое и параметрические уравнения прямой на плоскости. 2. Дано уравнение прямой
3. Дано уравнение прямой 4. Уравнение прямой задано в виде 5. Что определяет на плоскости а) 6. Найти общее уравнение прямой, проходящей через точку 7. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точки 8. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 9. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 10. Выяснить взаимное расположение двух прямых 11. Выяснить взаимное расположение двух прямых 12. Найти точку пересечения двух прямых 13. Пусть точки ___________________________________________________________________________
Домашнее задание. 1. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точки 2. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 3. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 4. Найти точку пересечения двух прямых
Фдз 13. Комплексные числа. Комплексные числа в алгебраической форме. Сравнение и изображение комплексных чисел на комплексной плоскости. Комплексное сопряжение. Сложение, умножение, деление комплексных чисел. Модуль, аргумент комплексного числа. Тригонометрическая и показательная формы записи комплексного числа. Возведение в целую степень и извлечение корня из комплексного числа.
1. Записать комплексное число в алгебраической форме. Дать определения действительной и мнимой части, модуля и аргумента комплексного числа. 2. Найти действительную и мнимую части комплексных чисел
Изобразить эти числа на комплексной плоскости. 3. Даны числа 4. Найти 5. Вычислить 6. Найти модуль и главное значение аргумента чисел:
7. Найти тригонометрическую и экспоненциальную формы записи комплексных чисел из задания 6. 8. Найти 9. Найти в показательной форме все значения 10. Найти в показательной форме все значения
_______________________________________________________________________
Домашнее задание. 1. Найти действительную и мнимую части, модуль и аргумент следующих комплексных чисел: 2. Найти 3. Найти все значения
Фдз 14. Многочлены. Корни многочлена, их кратность. Деление многочлена на многочлен (алгоритм Евклида). Целая и дробная части отношения двух многочленов.
Теорема Безу. Основная теорема алгебры многочленов. Многочлены с действительными коэффициентами, их разложение на множестве действительных и комплексных чисел.
1. Найти степень многочленов, приведенных ниже: а) 2. Найти корни многочлена 3. Найти корни многочлена 4. Найти целую часть, остаток и дробную часть от деления многочлена 5. Найти целую часть, остаток и дробную часть от деления многочлена 6. Показать, что многочлен 7. Сформулировать теорему Безу. Выяснить с ее помощью, будет ли делится нацело многочлен 8. Написать в общем виде разложения многочлена на множестве комплексных и на множестве действительных чисел. 9. Найти разложения многочлена 10. Найти разложения многочлена
______________________________________________________________________
Домашнее задание. 1. Найти все корни многочлена 2. Найти целую и дробную части отношения 3. Найти разложения многочлена
Фдз 1. Матрицы. Операции над матрицами. Операции с матрицами: равенство матриц; умножение матрицы на число; сложение матриц; перемножение матриц. Транспонирование матрицы. Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица. Возведение квадратной матрицы в натуральную степень.
1. Для матриц
2. Для матриц
3. (в случае невыполнимости операции указать причину невыполнимости):
4.
Какие из приведенных выше матриц являются: 1) симметрическими; 2) диагональными; 3) треугольными; 4) единичными. ________________________________________________________________________
Домашнее задание. 1. Для заданных матриц найти
Фдз 2. Определители. Определитель Основные свойства определителей.
1. Установить четность (нечетность) перестановок: 2. Дать определение определителя 3. Записать правила Саррюса вычисления определителей 1-го, 2-го, 3-го порядков. 4. Вычислить по правилам Саррюса определители:
5. Сформулировать основные свойства определителей.
6. Почему можно не вычисляя указанных ниже определителей сразу сказать, что каждый из них равен нулю?
7. Вычислить определители: 8. Вычислить следующие определителя, сведя их к определителям треугольных матриц:
___________________________________________________________________________ Домашнее задание. 1. Определить четность перестановки 2. Даны квадратные матрицы
1) Вычислить определители матриц 2) Вычислить определитель матрицы
|
||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.145.241 (0.011 с.) |

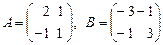 найти:
найти: .
. найти:
найти: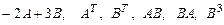 .
. . Выполнить те из операций, которые указаны ниже
. Выполнить те из операций, которые указаны ниже .
.

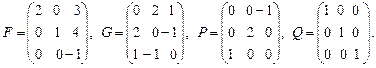

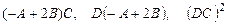 .
. -го порядка. Правила Саррюса вычисления определителей 2-го и 3-го порядков.
-го порядка. Правила Саррюса вычисления определителей 2-го и 3-го порядков. .
. го порядка.
го порядка. .
. .
. .
.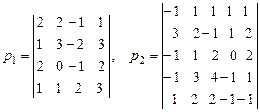 .
. .
.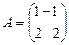 ,
,  ,
,  ,
,  .
.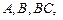 по правилам Саррюса.
по правилам Саррюса. с помощью свойств
с помощью свойств  определителей (сведя его к определителю матрицы треугольного вида).
определителей (сведя его к определителю матрицы треугольного вида). и алгебраические дополнения
и алгебраические дополнения  для матрицы
для матрицы  . Вычислить затем
. Вычислить затем 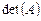 тремя способами:
тремя способами: и алгебраические дополнения
и алгебраические дополнения  для матрицы
для матрицы 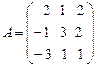 . Вычислить затем
. Вычислить затем  двумя способами:
двумя способами: .
. .
.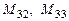 и алгебраические дополнения
и алгебраические дополнения 
 двумя способами:
двумя способами: .
.
 с заданными матрицами
с заданными матрицами 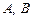 и неизвестной матрицей
и неизвестной матрицей  могут быть решены матричным методом (с помощью обратной матрицы)? Как проводится решение в этом случае?
могут быть решены матричным методом (с помощью обратной матрицы)? Как проводится решение в этом случае? двумя способами
двумя способами ;
;  .
. . Как называется такое уравнение прямой? Какой смысл имеет точка
. Как называется такое уравнение прямой? Какой смысл имеет точка  в этом уравнение? Какой геометрический смысл имеет вектор
в этом уравнение? Какой геометрический смысл имеет вектор  , координатами которого являются коэффициенты при
, координатами которого являются коэффициенты при 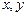 ?
? . Как называется такое уравнение прямой? Какой смысл имеет точка
. Как называется такое уравнение прямой? Какой смысл имеет точка  . Как называется такое задание прямой? Какой смысл имеет точка
. Как называется такое задание прямой? Какой смысл имеет точка  (точку, прямую) каждое из приведенных ниже равенств:
(точку, прямую) каждое из приведенных ниже равенств: б)
б)  в)
в)  , г)
, г) 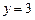 .
. перпендикулярно вектору
перпендикулярно вектору  , где
, где  .
. .
. параллельно прямой
параллельно прямой  .
. ,
,  .
. .
.
 - вершины треугольника
- вершины треугольника 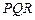 . Найти канонические уравнения следующих трех прямых: идущих по стороне
. Найти канонические уравнения следующих трех прямых: идущих по стороне  , по высоте, по медиане треугольника из вершины
, по высоте, по медиане треугольника из вершины  .
. .
. параллельно прямой
параллельно прямой  .
.
 ,
, 
 ,
,  .
. .
.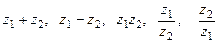 , если
, если  .
. , если
, если  .
. .
. и
и 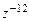 , если
, если 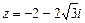 .
. .
. .
. . Изобразить эти числа на комплексной плоскости. Представить эти числа в показательной и тригонометрической формах.
. Изобразить эти числа на комплексной плоскости. Представить эти числа в показательной и тригонометрической формах. для комплексного числа
для комплексного числа 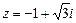 .
.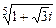 .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) -7.
; д) -7. и указать их кратность.
и указать их кратность.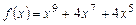 и указать их кратность.
и указать их кратность. на многочлен
на многочлен  .
. на многочлен
на многочлен  делится нацело на многочлен
делится нацело на многочлен  .
. многочленом
многочленом  ?
? на множестве комплексных и на множестве действительных чисел
на множестве комплексных и на множестве действительных чисел на множестве комплексных и на множестве действительных чисел, если известно, что
на множестве комплексных и на множестве действительных чисел, если известно, что  - корень кратности 2 этого многочлена.
- корень кратности 2 этого многочлена. и указать их кратность.
и указать их кратность. , где
, где  ,
,  .
. на множестве комплексных и на множестве действительных чисел.
на множестве комплексных и на множестве действительных чисел.


