
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фдз 5. Метод Гаусса решения линейных алгебраических систем.Содержание книги
Поиск на нашем сайте
Приведение системы к треугольному виду. Выделение свободных и базисных неизвестных. Получение общего решения системы или вывода о несовместности системы.
1. Какие линейные системы называются эквивалентными? 2. Что называется общим решением линейной системы? 3. Какие из приведенных ниже линейных систем являются системами треугольного вида:
4. Сформулировать элементарные преобразования линейных систем, переводящих заданную систему в эквивалентную ей систему. 5. Решить следующие системы треугольного вида, выделив в них свободные и базисные неизвестные:
6. В чем состоит основная идея метода Гаусса решения линейных алгебраических систем? 7. Решить методом Гаусса (или доказать несовместность) следующие системы:
________________________________________________________________________
Домашнее задание. Решить методом Гаусса следующие системы (или доказать несовместность): 1)
Фдз 6. Векторы в Вектор как направленный отрезок. Проекции вектора, длина вектора, направляющие косинусы. Сложение векторов. Умножение вектора на число. Условие коллинеарности двух векторов. Скалярное произведение векторов, его свойства, координатное выражение. Условие ортогональности двух векторов.
1. Найти а) Нарисовать полученные векторы 2. Найти 3. Сформулировать и записать условие коллинеарности двух векторов. 4. Выделить из приведенной системы векторов пары коллинеарных векторов:
5. Выяснить, лежат ли три точки 6. Дать определение скалярного произведения векторов и указать его свойства. 7. Записать координатное выражение скалярного произведения. 8. Пусть а) в) 9. Найти угол между векторами а) 10. Сформулировать и записать условие ортогональности двух векторов. 11. Даны векторы 12. Даны векторы
Домашнее задание. 1. Найти координаты, длину и направляющие косинусы вектора
2. При каких значениях параметров 3. 4.
5.
Фдз 7. Векторное и смешанное произведение векторов. Компланарные, некомпланарные тройки векторов. Ориентация тройки векторов. Векторное произведение: определение; свойства; координатное выражение. Смешанное произведение: определение; свойства; координатное выражение. Условие компланарности тройки векторов.
1. Какие тройки векторов называются компланарными? 2. Дать определение правой (левой) тройки векторов. 3. Определить с помощью соответствующих рисунков ориентацию следующих троек векторов: 1) 4. Дать определение векторного произведения 5. Записать формулу, по которой находится координатное выражение 6. Вычислить 1) 3) 7. Найти площадь параллелограмма, построенного на векторах 8. Найти площадь треугольника 9. Найти координаты орта 10. Дать определение смешанного произведения 11. Вычислить 1) С помощью найденных результатов определите ориентацию этих троек векторов. 12. Найти объем пирамиды 13. Выяснить, лежат ли точки на одной плоскости. ________________________________________________________________________
Домашнее задание. 1. Найти координаты вектора а) если 2. Вычислить площадь треугольника 3. Найти объем пирамиды 4. При каком значении параметра
Фдз 8. Прямая на плоскости. Различные виды задания прямой на плоскости. Основные задачи по нахождению прямой на плоскости. Взаимное расположение двух прямых. Угол между прямыми. Расстояние от точки до прямой.
1. Записать общее, каноническое и параметрические уравнения прямой на плоскости. 2. Дано уравнение прямой 3. Дано уравнение прямой 4. Уравнение прямой задано в виде 5. Что определяет на плоскости а) 6. Найти общее уравнение прямой, проходящей через точку 7. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точки 8. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 9. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 10. Выяснить взаимное расположение двух прямых 11. Выяснить взаимное расположение двух прямых 12. Найти точку пересечения двух прямых 13. Пусть точки ___________________________________________________________________________
Домашнее задание. 1. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точки 2. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 3. Найти каноническое, параметрические и общее уравнения прямой, проходящей через точку 4. Найти точку пересечения двух прямых
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.52 (0.006 с.) |

 ?
?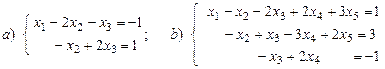 .
.
 ; 2)
; 2)  .
. ,
,  . Скалярное произведение векторов.
. Скалярное произведение векторов. , направляющие косинусы, орт вектора
, направляющие косинусы, орт вектора  в случаях:
в случаях: ; б)
; б) 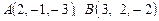 ; в)
; в)  .
. , если
, если  .
. .
. на одной прямой?
на одной прямой? - угол между векторами
- угол между векторами  . Найти скалярное произведение
. Найти скалярное произведение  в случаях:
в случаях: ; б)
; б)  ;
; .
. на вектор
на вектор 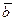 в случаях:
в случаях: ; б)
; б)  . При каком значении параметра
. При каком значении параметра 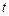 векторы
векторы  . При каких значениях параметра
. При каких значениях параметра  вектор
вектор  перпендикулярен вектору
перпендикулярен вектору  ?
? .
. точки
точки 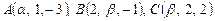 лежат на одной прямой?
лежат на одной прямой? - угол между
- угол между  . При каком значении
. При каком значении  векторы
векторы 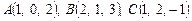 - вершины треугольника
- вершины треугольника  . Найти величину длины сторон этого треугольника и его углы при вершинах.
. Найти величину длины сторон этого треугольника и его углы при вершинах.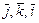 ; 2)
; 2)  ; 3)
; 3)  , где
, где  - орты осей
- орты осей  .
.
 векторов
векторов  ;
; .
. .
. с вершинами в точках
с вершинами в точках  .
.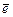 , перпендикулярного одновременно векторам
, перпендикулярного одновременно векторам  и такого, чтобы тройка
и такого, чтобы тройка  была правой.
была правой. векторов
векторов 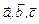 и указать его геометрический смысл.
и указать его геометрический смысл. ; 2)
; 2)  .
.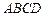 с вершинами
с вершинами  .
.
 , удовлетворяющего одновременно следующим условиям а), б), в):
, удовлетворяющего одновременно следующим условиям а), б), в):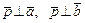 ; б)
; б)  ; в)
; в)  - левая тройка,
- левая тройка,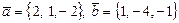 .
. .
. .
. лежат в одной плоскости?
лежат в одной плоскости? . Как называется такое уравнение прямой? Какой смысл имеет точка
. Как называется такое уравнение прямой? Какой смысл имеет точка  в этом уравнение? Какой геометрический смысл имеет вектор
в этом уравнение? Какой геометрический смысл имеет вектор  , координатами которого являются коэффициенты при
, координатами которого являются коэффициенты при 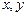 ?
? . Как называется такое уравнение прямой? Какой смысл имеет точка
. Как называется такое уравнение прямой? Какой смысл имеет точка  . Как называется такое задание прямой? Какой смысл имеет точка
. Как называется такое задание прямой? Какой смысл имеет точка  б)
б)  в)
в)  , г)
, г) 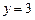 .
. перпендикулярно вектору
перпендикулярно вектору  , где
, где  .
. .
. параллельно прямой
параллельно прямой  .
. ,
,  .
. .
.
 - вершины треугольника
- вершины треугольника 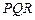 . Найти канонические уравнения следующих трех прямых: идущих по стороне
. Найти канонические уравнения следующих трех прямых: идущих по стороне  , по высоте, по медиане треугольника из вершины
, по высоте, по медиане треугольника из вершины  .
. .
. параллельно прямой
параллельно прямой  .
.



