Методом замены плоскостей проекций

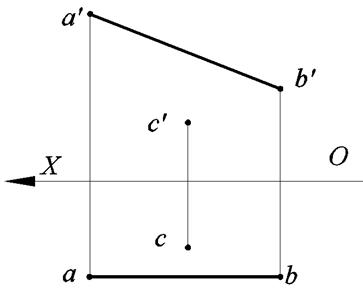
Для определения натуральной величины плоской фигуры необходимо преобразовать комплексный чертеж так, чтобы проецирующая плоскость в новой системе плоскостей стала плоскостью уровня.

Задача. Дано: плоскость Δ ABC – горизонтально проецирующая плоскость.

Преобразовать комплексный чертеж так, чтобы плоскость Δ ABC стала фронтальной плоскостью уровня.

Решение

1. Вводим новую плоскость проекции V ₁. Условия ввода плоскости V ₁: V ₁ ⊥ H ₁, V ₁⊥ Δ ABC.

2. Ось проекции X ₁ – горизонтальный след плоскости V _1. Проводим ось X ₁параллельно горизонтальной проекции плоскости Δ ABC на любом расстоянии от нее.

3. Проводим из точек a, b,и c линии связи (перпендикуляры к оси X ₁).

4. Откладываем Z_С, Z_А, Z_В по линиям связи соответственно точкам A, B, C от оси X ₁.

5. Получаем очки a ₁ ′, b ₁ ′, c ₁ ′. Соединяя полученные точки, получим новую проекцию плоскости Δ ABC равную натуральной величине Δ ABC.

Следовательно, в новой системе плоскостей плоскость занимает положение фронтальной плоскости уровня (рис. 83).

 

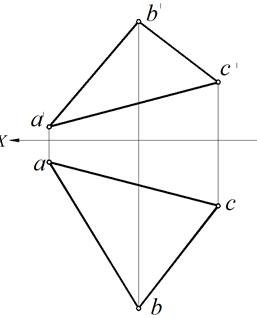
Задача. Определить натуральную величину плоскости, заданной треугольником DВA и угол наклона ее к горизонтальной плоскости проекций.

Решение. Анализируем графическое условие задачи – заданная плоскость занимает общее положение в пространстве. Следовательно, для определения натуральной величины плоскости треугольника необходимо осуществить два преобразования:

1. Преобразовываем заданную плоскость в проецирующую.

2. Преобразовываем заданную плоскость в плоскоть уровня.

 

Рис. 83. Преобразование горизонтально проецирующей плоскости во фронтальную плоскость уровня

 

Рис. 84. Определение натуральной величины плоскости ∆ АВD

Порядок выполнения графической части задачи (рис. 84):

1. Так как по условию задачи необходимо найти угол наклона плоскости треугольника к горизонтальной плоскости проекций, заданную плоскость преобразуем во фронтально проецирующую. Условия ввода плоскости V ₁: V ₁⊥ H, V ₁ ⊥ ∆ DВA.

1.1. Анализируем положение отрезков прямых, которыми задана плоскость треугольника: все они занимают общее положение.

1.2. Проводим в заданной плоскости горизонталь АN.

1.3. Перпендикулярно горизонтальной проекции горизонтали проводим новую ось проекций Х ₁на любом расстоянии от точки А.

1.4. Откладываем от оси Х ₁координаты Z_D, Z_B, Z_C вдоль линии связи точек В, С и D.

1.5. Получаем проекцию плоскости ∆ DВA в виде прямой линии.

1.6. На новую плоскость проекций V ₁ плоскость ∆ DВA отобразилась в впрямую линию, т. е.стала фронтально проецирующей плоскостью. На новой плоскости проекций V ₁ угол наклона плоскости треугольника DВA к горизонтальной плоскости проекций α отображен без искажения (рис. 84).

2. Для построения натуральной величины плоскости треугольника преобразовываем ее в горизонтальную плоскость уровня.

2.1. Вводим новую плоскость проекции Н ₁: V ₁ ⊥ H ₁, Н ₁ || ∆ DВA.

2.2. Ось проекции X ₂ – горизонтальный след плоскости Н ₁.Проводим параллельно прямой b ₁′ d ₁′ a ₁ ′ ось X ₂на любом расстоянии от нее.

2.3. Проводим из точек b ₁′, d ₁′, a ₁ ′ линии связи (перпендикуляры к оси X ₂).

2.4. Откладываем расстояния от точек а, b и d до оси Х ₁по линиям связи этих точек от X ₂ соответственно точкам A, B, D.

2.5. Получаем точки a ₁, b ₁, d ₁. Соединяя полученные точки, получим новую проекцию плоскости ∆ DВA равную натуральной величине ∆ DВA.

Следовательно, в новой системе плоскостей плоскость занимает положение горизонтальной плоскости уровня.

Библиографический список

 

1. Белякова, Е. И. Начертательная геометрия: практикум: учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый; под ред. П. В. Зеленого. – 2-е изд., испр. – Минск: Новое знание; Москва: ИНФРА-М, 2012. – 214, [10] с.: ил.

2. Дегтярев, В. М. Инженерная и компьютерная графика: учебник для студентов вузов / В. М. Дегтярев, В. П. Затыльникова. – М.: Академия, 2010. – 240 с. – (Высшее профессиональное образование).

3. Левицкий, В. С. Машиностроительное черчение и автоматизация выполнения чертежей: учебник для втузов / В. С. Левицкий. – 8-е изд., перераб. и доп. – М.: Высш. школа, 2007. – 435 с.: ил.

4. Нартова, Л. Г. Начертательная геометрия: учебник для вузов / Л. Г. Нартова, В. И. Якунин. – 3-е изд., стер. – Москва: Академия, 2011. – 192 с.: ил.

5. Чекмарев, А. А. Начертательная геометрия и черчение: учеб. для бакалавров / А. А. Чекмарев. – М.: Юрайт, 2012. – 472 с.

6. Чекмарев, А. А. Начертательная геометрия и черчение: учеб. для вузов / А. А. Чекмарев. – 2-е изд., перераб. и доп. – М.: ВЛАДОС, 2005. – 472 с.

ПРИЛОЖЕНИЕ 1

Варианты * заданий к домашней работе № 1

Содержание домашней работы

1. На формате А4 выполнить задачи. Все построения сохранить.

2. Оформит титульный лист и все подшить в папку формата А4.

 

БИЛЕТ № 1

Задача 1. Построить горизонтальную проекцию отрезка прямой АВ с углом наклона 30º к фронтальной плоскости проекций, если точка В расположена на оси ОХ на расстоянии 20 мм от профильной плоскости проекций. А (70;?; 30). На прямой АВ построить точку С, отстоящую от точки А на расстоянии 15 мм.

 

Задача 2. Определить расстояние от точки В до стороны АС в плоскости треугольника АВС.

 

 

Задача 3. Определить угол наклона заданной плоскости к горизонтальной плоскости проекций по линии ската.

 

БИЛЕТ № 2

Задача 1. Построить фронтальную проекцию отрезка прямой ВС с углом наклона 45ºк горизонтальной плоскости проекций, если точка С расположена в плоскости Н на расстоянии 20 мм от профильной плоскости проекций и 10 мм от фронтальной плоскости проекций. В (70; 30;?). На прямой ВС построить точку А, отстоящую от точки С на расстоянии 20 мм.

 

Задача 2. В плоскости треугольника АВС построить квадрат со стороной 20 мм, лежащей на линии ската плоскости треугольника.

 

 

Задача 3. Определить угол наклона заданной плоскости к фронтальной плоскости проекций по линии наибольшего наклона.

 

БИЛЕТ № 3

Задача 1. Определить периметр треугольника АВС.

А (100; 30; 0), В (60; 30; 50), С (20; 50; 20).

 

Задача 2. В плоскости треугольника АВС построить прямоугольный равнобедренный треугольник с катетом 30 мм, лежащим на линии ската плоскости треугольника.

 

 

Задача 3. Построить ромб АВСD, диагональ которого CD длиной 50 мм лежит на прямой МN. Определить угол наклона построенной плоскости ромба к фронтальной плоскости проекций.

 

БИЛЕТ № 4

Задача 1. Определить расстояние от точки А до прямой ВС.

А (100; 50; 30), В (60; 10; 50), С (60; 40; 0).

 

Задача 2. Через точку А провести прямую АМ, параллельную фронтальной плоскости проекций и пересекающую прямую ВС. Определить угол наклона к фронтальной плоскости проекций плоскости, заданной прямыми АМ и ВС.

 

Задача 3. Построить прямоугольный равнобедренный треугольник АВС, если катет ВС лежит на прямой МN.

 

БИЛЕТ № 5

Задача 1. Определить расстояние от точки А до прямой ВС.

А (100; 50; 30), В (60; 10; 50), С (60; 40; 0).

 

Задача 2. Через точку А провести прямую, пересекающую отрезок ВС в точке К, делящей отрезок ВС в отношении 3:2 начиная от точки В.

 

 

 

Задача 3. Определить угол наклона заданной плоскости к фронтальной плоскости проекций по линии наибольшего наклона.

 

 

БИЛЕТ № 6

Задача 1. Построить фронтальный след прямой ВС. Определить угол наклона заданной прямой к фронтальной плоскости проекций.

В (30; 40; 40), С (60; 10; 30).

 

Задача 2. Определить взаимное положение прямых.

 

 

Задача 3. Определить угол наклона заданной плоскости к горизонтальной плоскости проекций по линии ската.

 

 

 

БИЛЕТ № 7

 

Задача 1. Построить горизонтальный след прямой АВ. Определить угол наклона заданной прямой к горизонтальной плоскости проекций.

А (30; 40; 40), В (60; 10; 10).

Задача 2. Определить расстояние между прямыми.

 

 

 

Задача 3. Определить угол наклона заданной плоскости к фронтальной плоскости проекций по линии наибольшего наклона.

 

БИЛЕТ № 8

 

Задача 1. Через точку С (20; 20; 20) провести 2 отрезка прямых: 1-й параллелен отрезку АВ, 2-й пересекает АВ в середине.

А (30; 40; 40), В (60; 10; 10).

 

Задача 2. Построить прямоугольный треугольник АВС, если задан катет АВ, а катет ВС длиной 40 мм лежит на прямой MВ.

 

 

 

Задача 3. Определить угол наклона заданной плоскости к фронтальной плоскости проекций по линии наибольшего наклона.

 

 

 

БИЛЕТ № 9

 

Задача 1. На прямой АВ построить точку С, отстоящую то точки В на расстояние 20 мм.

А (20; 30; 50), В (70; 0; 30).

 

Задача 2. Построить прямоугольник АВСD, если дана сторона АВ, а сторона ВС длиной 20 мм лежит на прямой MВ.

 

 

 

Задача 3. Определить угол наклона заданной плоскости Р к горизонтальной плоскости проекций по линии ската.

 

 

 

 

БИЛЕТ № 10

 

Задача 1. На прямой АВ построить точку, лежащую в горизонтальной плоскости проекций.

А (70; 30; 20), В (100; 10; 50).

 

Задача 2. Построить ромб АВСD, если диагональ ВD длиной 40 мм лежит на прямой MN.

 

 

Задача 3. Определить угол наклона заданной плоскости Р (А, ВС) к горизонтальной плоскости проекций.

 

 

 

БИЛЕТ № 11

Задача 1. Определить расстояние от точки C до отрезка прямой AB.

A (100; 10; 30), B (60; 40; 30), C (80; 0; 60).

 

Задача 2. Заключить отрезок прямой AB в профильно проецирующую плоскость P,выразив эту плоскость следами. Указать углы наклона плоскости P к плоскостям V и H.

 

 

 

Задача 3. Определить угол наклона заданной плоскости (АВ ∩ СD) к плоскости проекций H по линии ската.

БИЛЕТ № 12

Задача 1. Определить расстояние от точки A до отрезка прямой BC. Построить фронтальный след прямой BC.

A (60; 40; 40), B (80; 10; 30), C (30; 40;30).

Задача 2. Построить равнобедренный треугольник ABC с вершиной в точке A и основанием BC, равным 40 мм и лежащим на прямой MN.

 

Задача 3. Определить угол наклона заданной плоскости к плоскости проекций H по линии ската.

 

БИЛЕТ № 13

Задача 1. Определить натуральную величину отрезка прямой AB и угол наклона его к плоскости проекций V. Построить точку C, конкурирующую с точкой A и расположенную ниже точки A на 30 мм.

A (70; 50; 50), B (10; 0; 30).

 

Задача 2. Найти расстояние от точки A до отрезка прямой BC.

 

 

Задача 3. Определить угол наклона плоскости P, заданной параллельными прямыми AB и CD, к плоскости V по линии наибольшего наклона.

 

 

БИЛЕТ № 14

Задача 1. На расстоянии 20 мм от плоскости V провести отрезок фронтальной прямой, пересекающей отрезки AB и CD. Найти угол наклона проведенного отрезка прямой к горизонтальной плоскости проекций.

A (90; 10; 50), B (90; 50; 10), C (70; 40; 40), D (35; 15; 10).

 

Задача 2. Построить ромб ABCD, вершина которого находится в точке A, а диагональ BD, равная 55 мм, лежит на отрезке MN.

 

 

Задача 3. Определить натуральную величину и угол наклона к плоскости V отрезка AB.

БИЛЕТ № 15

Задача 1. Через точку A провести профильную прямую AB (восходящую), угол наклона к плоскости H равен 45º, а через точку C – параллельную ей прямую. Определить угол наклона отрезка AB к плоскости V.

A (35; 10; 15), C (20; 15; 35).

 

Задача 2. Построить равнобедренный треугольник с вершиной A, расположенной на отрезке MN и основанием BC, равным 40 мм, расположенном на отрезке EF. Точка К – основание высоты треугольника.

 

 

Задача 3. В заданной плоскости провести прямую MN общего положения и определить угол наклона этой прямой к фронтальной плоскости проекций.

БИЛЕТ № 16

Задача 1. Через точку A провести фронталь с углом наклона 30º к плоскости H с натуральной величиной 45 мм, а через точку C – прямую, ей параллельную и равную половине. Построить горизонтальный след прямой CD.

A (80; 15; 10), C (30; 20; 15).

 

Задача 2. Построить проекции квадрата ABCD, одна из сторон которого AB, а вторая – BC, наклонена к плоскости V под углом 30º.

Задача 3. Определить угол наклона к плоскости H плоскости, заданной параллельными прямыми.

 

 

 

 

БИЛЕТ № 17

Задача 1. По заданной горизонтальной проекции отрезка AB построить фронтальную и профильную проекции отрезка АВ с натуральной величиной 50 мм. Определить угол наклона прямой AB к плоскости проекций H.

A (50; 10; 10), B(50;50;?).

Задача 2. Построить горизонтальный след плоскости, заданной треугольником ABC и определить ее угол наклона к плоскости H по линии ската.

Задача 3. Построить проекции ромба ABCD, если дана вершина А, а диагональ ВD длиной 40 мм лежит на прямой ЕF.

БИЛЕТ № 18

Задача 1. Через точку K провести отрезок прямой линии, пересекающей отрезок AB в точке, делящей его в отношении 1:3. Определить угол наклона к плоскости H построенного отрезка.

A (100; 15; 20), B (50; 45; 65), K (35; 10; 40).

Задача 2. Построить проекции прямоугольного треугольника CDE, катет DE которого лежит на прямой AB и равен 25 мм.

 

 

Задача 3. Определить угол наклона плоскости треугольника ABC к плоскости проекций V по линии наибольшего наклона.

БИЛЕТ № 19

Задача 1. Построить фронтальную проекцию отрезка AB с натуральной величиной 60 мм, если точка A расположена на горизонтальной плоскости проекций на расстоянии 20 мм от плоскости V и 90 мм от плоскости W, а точка B имеет координаты B (40; 35;?). Определить угол наклона отрезка AB к плоскости H.

Задача 2. Построить проекции квадрата ABCD, если известна вершина A, а сторона BC лежит на прямой EF.

 

Задача 3. Через точку A провести линию ската плоскости S, заданной горизонталью и фронталью. Точка A принадлежит плоскости S. Определить угол наклона плоскости S к плоскости H.

 

 

 

БИЛЕТ № 20

Задача 1. Построить горизонтальную проекцию отрезка AB с натуральной величиной 50 мм, если точка A расположена на фронтальной плоскости проекций на расстоянии 30 мм от плоскости Н и 70 мм от плоскости W, а точка B имеет координаты B (20;?; 50). Определить угол наклона отрезка AB к плоскости V.

Задача 2. В плоскости треугольника ABC построить центр описанной окружности.

 

Задача 3. Определить угол наклона плоскости, заданной пересекающимися прямыми АВ и ВС,к плоскости проекций H по линии ската.

 

 

БИЛЕТ № 21

Задача 1. Через точку A провести горизонталь длиной 40 мм с углом наклона 30º к плоскости V, а через точку C – прямую, ей параллельную и равную половине. Построить фронтальный след прямой CD.

A (80; 15; 10), C (30; 20; 15).

 

Задача 2. Построить горизонтальную проекцию отрезка АВ с углом наклона к плоскости проекций Н 30º.

Задача 3. Построить проекции квадрата, лежащего в заданной плоскости АВС, если его сторона длиной 30 мм лежит на линии ската заданной плоскости.

 

БИЛЕТ № 22

Задача 1. Через точку A провести профильную прямую AB (восходящую), угол наклона к плоскости H равен 45º, а через точку C – параллельную ей прямую. Определить угол наклона отрезка AB к плоскости V.

A (35; 10; 15), C (20; 15; 35).

 

Задача 2. Построить равнобедренный треугольник с вершиной A, расположенной на отрезке MN и основанием BC, равным 40 мм, расположенном на отрезке EF. Точка К – основание высоты треугольника.

 

Задача 3. В заданной плоскости провести прямую MN общего положения и определить угол наклона этой прямой к фронтальной плоскости проекций.

БИЛЕТ № 23

Задача 1. Через точку A провести профильную прямую AB (восходящую), угол наклона к плоскости V равен 30º, а через точку C – параллельную ей прямую. Определить угол наклона отрезка AB к плоскости Н.

A (35; 10; 15), C (20; 15; 35).

 

Задача 2. Построить центр тяжести треугольника АВС и записать его координаты. Определить расстояние от точки до построенного центра тяжести.

 

 

 

Задача 3. В заданной плоскости треугольника АВС построить прямоугольный равнобедренный треугольник, если один из катетов длиной 20 мм лежит на линии ската.

 

 

БИЛЕТ № 24

Задача 1. Через точку A провести профильную прямую AB (восходящую), угол наклона к плоскости H равен 45º, а через точку C – параллельную ей прямую. Определить угол наклона отрезка AB к плоскости V.

A (35; 10; 15), C (20; 15; 35).

 

Задача 2. Построить проекции квадрата АВСD с вершиной в точке A и диагональю ВD, лежащей на отрезке MN.

 

Задача 3. Построить горизонтальную проекцию плоскости заданного многоугольника АВСDEF. Определить угол наклона к горизонтальной плоскости проекций заданного многоугольника АВСDEF по линии ската.

 

БИЛЕТ № 25

Задача 1. Определить периметр треугольника АВС.

A (80; 10; 15), В (20; 10; 50), C (50; 50; 15).

 

Задача 2. Построить параллелограмм АВСD, если точка Е является точкой пересечения диагоналей параллелограмма.

 

 

 

Задача 3. В плоскости треугольника АВС построить квадрат, сторона которого длиной 30 мм лежит на фронтали плоскости треугольника АВС.

 

БИЛЕТ № 26

Задача 1. На расстоянии 60 мм от плоскости W провести отрезок профильной прямой уровня, пересекающей отрезки AB и CD. Определить натуральную величину построенного отрезка.

A (80; 20; 30), В (50; 10; 20), C (70; 30; 40), D (10; 15; 10).

Задача 2. Построить проекции прямоугольного треугольника ABC, один катет которого AB, второй BC, равный 40 мм, лежит на отрезке BM.

 

 

 

Задача 3. Построить недостающую проекцию точки K, лежащей в плоскости P (профильной плоскостью проекций не пользоваться).

 

БИЛЕТ № 27

Задача 1. Построить горизонтальную проекцию отрезка MK с углом наклона 30º к плоскости V. Точка M имеет координаты (70; 20; 0), а точка K расположена на расстоянии 50 мм от плоскости H и 20 мм от плоскости W. Построить точку A, конкурирующую с точкой K и расположенную за точкой K на 20 мм.

Задача 2. Построить проекции квадрата, если дана диагональ AC, а диагональ BD наклонена к плоскости V под углом 60º.

Задача 3. Определить угол наклона плоскости параллелограмма ABCD к плоскости H по линии ската.

 

 

БИЛЕТ № 28

Задача 1. Построить фронтальную проекцию отрезка CM с натуральной величиной равной 60 мм. Точка M расположена на плоскости H на расстоянии 10 мм от плоскости V и 200 мм от плоскости W, а точка C имеет координаты (50; 30;?). На отрезке прямой МС построить точку A отстоящую от точки M на 30 мм.

Задача 2. Найти расстояние между параллельными прямыми AB и CD.

Задача 3. В плоскости, заданной треугольником ABC, построить фронтальную проекцию отрезка MN. Определить натуральную величину отрезка MN и угол наклона отрезка прямой MN к фронтальной плоскости проекций.

БИЛЕТ № 29

Задача 1. Определить расстояние от точки А до прямой ВС.

А (50; 60; 50), В (100; 40; 50), С (60; 40; 0).

 

Задача 2. Через точку А провести прямую АМ, параллельную горизонтальной плоскости проекций и пересекающую прямую ВС. Определить угол наклона к горизонтальной плоскости проекций плоскости, заданной прямыми АМ и ВС.

 

 

Задача 3. Построить проекции квадрата АВСD, если дана вершина А, диагональ ВD лежит на прямой МN.

 

БИЛЕТ № 30

Задача 1. Приняв заданный отрезок прямой AB за линию ската искомой плоскости Р, провести через точку А горизонталь плоскости Р длиной 50 мм и определить угол наклона построенной плоскости Р к плоскости проекций H.

А (80; 30; 50), В (20; 50; 10).

Задача 2. Через точку А провести горизонталь, пересекающую прямую ВС.

 

 

Задача 3. Определить центр тяжести треугольника АВС и записать его координаты. Определить угол наклона плоскости треугольника АВС к плоскости H по линии ската.

 

 

ПРИЛОЖЕНИЕ 2

Пример выполнения домашней работы № 1

Министерство образования и науки РФ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Уральский федеральный университет имени первого Президента России Б.Н.Ельцина» Нижнетагильский технологический институт (филиал)   Департамент технологического (общего) образования Кафедра «ИТ»   Дисциплина: Инженерная графика   (Начертательная геометрия и инженерная графика, Компьютерная графика, Инженерная и компьютерная графика)     ДОМАШНЯЯ РАБОТА № 1 БИЛЕТ № 31   ГРУППА СТ-140002     СТУДЕНТ Иванова А. И.     ПРЕПОДАВАТЕЛЬ Аляутдинова Л. Е.   Нижний Тагил 20…

Задача 1.Через точку А провести 2 отрезка прямой линии: первый пересекает отрезок СB в точке, делящей его в отношении 1:2, второй – параллелен заданному отрезку СВ. С (100; 20; 20), B (50; 45; 65), А (35; 10; 40). Решение:

Задача 2. Построить проекции квадрата АВСD, если дана сторона АВ, а сторона СD наклонена к фронтальной плоскости проекций под углом 30º.   Решение:       Задача 3. Определить угол наклона плоскости, заданной треугольником ВAD, к фронтальной плоскости проекций по линии наибольшего наклона.       Решение:

ПРИЛОЖЕНИЕ 3

Выполнение эпюра № 3

ЗАДАНИЕ

 

Определить угол наклона параллелограмма АВСD к плоскости проекций Н или V. Построить биссектрису угла плоскости параллелограмма, указанного в задании варианта.