
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение СЛУ методом Гаусса. Теорема Кронекера-Капелли.Содержание книги
Поиск на нашем сайте
В общем виде будем рассматривать систему m линейных уравнений с n переменными. В общем виде:
Эту же систему можно записать в матричном виде: А*Х=В, где А*Х=О – однородная СЛУ, где
Решение СЛУ методом Гаусса. Преобразование расширенной матрицы [A|B] в матрицу [C|D] из теоремы в процессе преобразований П1-П4 называется СЛУ методом Гаусса-Жордано. Его также называют методом последовательного исключения переменных. Система А*Х=В переходит в систему C*Y=D, где расширенная матрица
В левом верхнем углу получаем единичную матрицу, получаем 0 ниже главной диагонали этой матрицы. Это называется прямой ход метода Гаусса. Дальнейшее получение 0 выше главной диагонали называется обратный ход. Теорема Кронекера-Капелли: Если ранг матрицы А равен рангу расширенной матрицы [A|B], то систнма имеет решения. Если ранг матрицы [A|B] больше ранга матрицы А, то система решений не имеет. Вывод: В процессе преобразований мы получаем расширенную матрицу [C|D], тогда r(A)=r(C)=det Если все свободные члены dr+1=dr+2=dm=0, то система имеет решения. Это очевидно. последние строчки можно отбросить. Предположим, что одно из чисел dr+1; dr+2; dm≠0. Возьмем для примера dr=1. 0*х1+0*х2+…+0*хn=1 0=1 ложно. Эта СЛУ не имеет решений. Покажем, что ранг расширенной матрицы на 1 больше ранга матрицы А. L= Получив расширенную матрицу [C|D] мы можем исследовать СЛУ. Пусть r<n, тогда система имеет бесконечное множество решений.
Свободные переменные yr+1… -- становятся свободными, а остальные переменные становятся зависимыми. Давая различные значения свободным переменным, получаются различные значения зависимых переменных. Теперь понятно, что система имеет бесконечное множество решений. Мы рассматриваем случаи, когда система имеет решения, т.е. ранг матрицы и ранг расширенной матрицы равны. Это означает, что в матрице [C|D] ниже единичной матрицы все строки нулевые, т.е. эквивалентны уравнениям 0=0 0=0 0=0 0=0 … 0=0, поэтому их можно удалить.
Рассмотрим случай, когда r=n. В таком случае матрица [C|D] имеет вид: слева от черты находится единичная матрица. Читаем систему Пусть r=n и число уравнений совпадает с числом переменных, тогда в матрице [C|D] слева от вертикальной черты стоит единичная матрица. Нулевых строк нет. Матрица имеет единственное решение
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.189.236 (0.006 с.) |


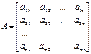
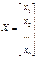 -- столбец переменных
-- столбец переменных 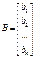
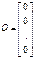 . Очевидно, такая система имеет хотя бы одно тривиальное решение.
. Очевидно, такая система имеет хотя бы одно тривиальное решение. 
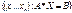 -- множество решений СЛУ. Если существует хотя бы одно решение, то СЛУ называется совместной. Иначе это несовместная СЛУ.
-- множество решений СЛУ. Если существует хотя бы одно решение, то СЛУ называется совместной. Иначе это несовместная СЛУ.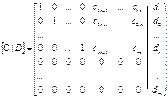
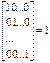
 det(L)=dm=1 r(A|B)=R(C|D)=r+1=r(A)+1
det(L)=dm=1 r(A|B)=R(C|D)=r+1=r(A)+1
 zr+1; zr+2; …; zn – свободные параметры. Давая им произвольные значения получаем бесконечное множество решений.
zr+1; zr+2; …; zn – свободные параметры. Давая им произвольные значения получаем бесконечное множество решений.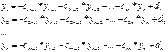

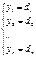 . Это единственные решения системы.
. Это единственные решения системы.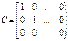
 .
.


