
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение векторного пространства. Линейные операции над векторами. Основные свойства.Содержание книги
Поиск на нашем сайте
Rn – n-мерное пространство (х1, х2, …, хn) – точки из пространства Rn R – множество действительных чисел. R2 – плоскость R3 – 3-х мерное пространство
Определение вектора и векторного пространства: А, В определяют перемещение в пространстве из точки А в точку В, которые называются векторами. Эти перемещения(векторы) определяются с точностью до параллельного переноса, т.е. равенство между векторами задается следующей формулой:
Множество всех векторов называют векторным пространством. Замечание: Это определение будет вектор как отрезок и введенное равенство определяют направляющий отрезок с точностью до параллельного переноса.
a={a1; a2; …; an} a определяется как перенос(параллельный) пространства, т.е. как отображение пространства на себя. Мы получаем: Для нас вектор – перемещение из точки в точку В.
Линейные свойства векторов: 1. 2. 3. Из этих определений следует правило вычитания векторов: 4. 5. Нетрудно доказать следующие свойства векторов: 6. а+0=0+а=а a+b=b+a – переместительный закон сложения (a+b)+c=a+(b+c) – ассоциативность сложения λ(a+b)= λ*a+ λ*b и т.д. Из определения сложения и вычитания векторов получаем следующие правила: параллелограмма, треугольника и многоугольника:
Правило многоугольника e=a+b+c+d
Правило многоугольника: Направляем векторы один за другим, соединяя начало первого с концом последнего.
Нетрудно проверить все эти свойства на плоскости и в пространстве. Линейная зависимость и независимость векторов. λ1а1+ λ2а2+…+ λnаn – линейная комбинация векторов а1, а2, …, аn. Если λ1а1+ λ2а2+…+ λnаn=0 и хотя бы одно из чисел λ1, λ2,..., λn не равно 0, то такую линейную комбинацию называют нетривиальной линейной комбинацией. Линейная зависимость векторов. Если существует нетривиальная линейная комбинация λ1а1+ λ2а2+…+ λnаn, то векторы а1, а2, …, аn называют линейно зависимыми. В этом случае один из векторов является линейной комбинацией других векторов. Пусть λn≠0 => Линейная независимость векторов. а1, а2, …, аn называются линейно независимыми, если не существует нетривиальной линейной комбинации этих векторов. Для любой линейной комбинации получаем: λ1а1+ λ2а2+…+ λnаn=0 => Линейно зависимые вектора называются компланарными. λ1а1+ λ2а2+λ3а3=0 (1) а3=с1а1+с2а2(λ3≠0) Если эти векторы отложить один за другим, то получится замкнутая фигура. Поэтому компланарные векторы параллельны одной плоскости. В условии (1) содержится условие компланарности векторов. Два линейно зависимых вектора называют коллинеарными. λ1а1+ λ2а2 =0 – нетривиальная комбинация b=λа – условие коллинеарности векторов.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.104 (0.007 с.) |

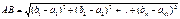 -- расстояние между двумя точками. Для 2-х мерного пространства это обычная теорема Пифагора.
-- расстояние между двумя точками. Для 2-х мерного пространства это обычная теорема Пифагора.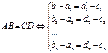 Общий вид таких векторов записывается в виде
Общий вид таких векторов записывается в виде  , где а1;а2;…;аn – координаты вектора или проекции вектора а на оси х1;х2;…;хn.
, где а1;а2;…;аn – координаты вектора или проекции вектора а на оси х1;х2;…;хn. АВ=CD=PQ
АВ=CD=PQ .
.
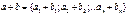
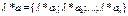
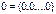 -- нулевой вектор
-- нулевой вектор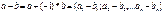
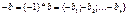 -- определение противоположного вектора.
-- определение противоположного вектора. Правило параллелограмма a+b
Правило параллелограмма a+b Правило треугольника a+b
Правило треугольника a+b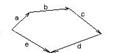
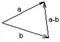 b+(a-b)=a
b+(a-b)=a a+(b-a)=b
a+(b-a)=b
 .
.


