
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем линейных уравнений методом Жордана-Гаусса
Как уже говорилось, метод Жордана-Гаусса состоит в приведении системы к равносильной системе канонического вида. Рассмотрим суть этого метода на следующих примерах. Пример. Решить методом Жордана-Гаусса систему Решение. Отметим, что в предыдущем параграфе эта система была решена методом Гаусса, для чего она элементарными преобразованиями приводилась к ступенчатому виду. Теперь, в соответствии с методом Жордана-Гаусса, приведем ее к каноническому виду соответствующими элементарными преобразованиями строк расширенной матрицы системы. Расширенная матрица системы имеет вид Пример. Решить методом Жордана-Гаусса систему Решение. Приведем расширенную матрицу системы элементарными преобразованиями строк (и вычеркиванием чисто нулевых строк, если таковые появятся) к канонической матрице:
~ Последняя матрица − каноническая и является расширенной матрицей следующей системы в канонической форме (эквивалентной исходной системе):
Придавая свободным переменным любые значения и вычисляя затем базисные переменные из общего решения, будем получать решения исходной системы. Эти решения называются ее частными решениями, которых, очевидно, бесконечно много. Если положить, например,
Придавая паре переменных Однородные системы Исследуем произвольную однородную систему линейных уравнений:
В этом случае ранги основной и расширенной матриц совпадают ( Утверждение 1. Однородная система линейных уравнений имеет ненулевые решения (причем бесконечное число их) в том и только в том случае, когда ранг ее основной матрицы меньше числа неизвестных: Рассмотрим случай, когда число уравнений в однородной системе совпадает с числом неизвестных (
На основании предыдущего Утверждения 1 легко доказать следующее Утверждение 2. Однородная система из n линейных уравнений с n неизвестными имеет ненулевые решения только в том случае, если определитель основной матрицы этой системы Найдем вид общего решения таких систем на примере трех уравнений с тремя неизвестными: (9) Как отмечалось, однородная система всегда совместна, поскольку всегда имеет нулевое решение
(10) Можно показать, что системы (9) и (10) эквивалентны (т.е. имеют одни и те же решения), а потому найдя общее решение системы (10), получим и общее решение исходной системы (9). Перенесем в (10) слагаемые с переменной
как систему двух уравнений с двумя неизвестными x и y при произвольном значении переменной (11) где (12) При каждом числовом значении параметра t эти формулы дают одно из решений системы (например, при Пример. Найти общее решение системы Решение. По формулам (12) получаем
Иногда требуется из бесконечного множества решений однородной системы выделить решения, обладающие каким-либо дополнительным свойством. Пример. Найти решение предыдущей системы Решение. Как было только что выяснено, общее решение системы имеет вид: Замечание. Фактически мы нашли решение системы уравнений
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.013 с.) |
 .
. . Такая матрица элементарными преобразованиями строк ранее (в параграфе «Элементарные преобразования матриц. Ранг матрицы») уже была приведена к эквивалентной канонической матрице:
. Такая матрица элементарными преобразованиями строк ранее (в параграфе «Элементарные преобразования матриц. Ранг матрицы») уже была приведена к эквивалентной канонической матрице:  . Эта матрица является расширенной матрицей для следующей системы канонического вида:
. Эта матрица является расширенной матрицей для следующей системы канонического вида:  . Решение этой системы очевидно. Таким образом, решение исходной системы:
. Решение этой системы очевидно. Таким образом, решение исходной системы: 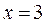 ,
,  ,
, 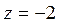 .
. .
.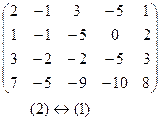 ~
~  ~
~ 
 ~
~ 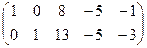 .
. . Переменные, коэффициенты при которых соответствуют ненулевым диагональным элементам (а это единицы для канонических матриц) расширенной матрицы системы, называются базисными переменными, а остальные переменные называются свободными переменными. Базисные переменные (в нашей системе это
. Переменные, коэффициенты при которых соответствуют ненулевым диагональным элементам (а это единицы для канонических матриц) расширенной матрицы системы, называются базисными переменными, а остальные переменные называются свободными переменными. Базисные переменные (в нашей системе это  и
и  ) легко выражаются через свободные (в нашей системе это
) легко выражаются через свободные (в нашей системе это 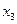 и
и  ). Проделывая это для данной системы, получаем то, что называется общим решением системы:
). Проделывая это для данной системы, получаем то, что называется общим решением системы: ,
,  .
. и
и  , то из общего решения получаем
, то из общего решения получаем  и
и  Таким образом, одно из частных решений исходной системы имеет вид:
Таким образом, одно из частных решений исходной системы имеет вид:  ,
,  , а
, а  . Тогда выписанное выше общее решение можно записать в виде:
. Тогда выписанное выше общее решение можно записать в виде: ,
,  ,
,  всевозможные числовые значения и подставляя их в общее решение, получим все решения исходной системы.
всевозможные числовые значения и подставляя их в общее решение, получим все решения исходной системы. .
. ). Это следует из того, что расширенная матрица получается из основной добавлением нулевого столбца, а потому среди ненулевых миноров расширенной матрицы не может быть таких, которые не входили в основную матрицу. По теореме Кронекера-Капелли (см. параграф «Исследование общих систем линейных уравнений. Теорема Кронекера-Капелли») из этого следует, что любая однородная система совместна. Очевидно, что одним из ее решений всегда является решение
). Это следует из того, что расширенная матрица получается из основной добавлением нулевого столбца, а потому среди ненулевых миноров расширенной матрицы не может быть таких, которые не входили в основную матрицу. По теореме Кронекера-Капелли (см. параграф «Исследование общих систем линейных уравнений. Теорема Кронекера-Капелли») из этого следует, что любая однородная система совместна. Очевидно, что одним из ее решений всегда является решение  , которое называется нулевым (или тривиальным) решением однородной системы. Учитывая теорему Кронекера-Капелли, легко найти условия, при которых однородная система имеет и ненулевые решения.
, которое называется нулевым (или тривиальным) решением однородной системы. Учитывая теорему Кронекера-Капелли, легко найти условия, при которых однородная система имеет и ненулевые решения. .
. ):
): .
. .
. .
. . Если определитель основной матрицы системы
. Если определитель основной матрицы системы 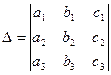
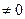 , то это нулевое решение единственно. Пусть
, то это нулевое решение единственно. Пусть  . Это означает, ранг
. Это означает, ранг  основной матрицы системы не может быть равен 3, а потому
основной матрицы системы не может быть равен 3, а потому  . Предположим, что ранг основной матрицы
. Предположим, что ранг основной матрицы  . Это означает, что хотя бы один из миноров второго порядка не равен 0. Пусть, например, минор
. Это означает, что хотя бы один из миноров второго порядка не равен 0. Пусть, например, минор  , а потому является базисным минором. В системе (9) оставим только те уравнения, коэффициенты которых участвуют в образовании базисного минора. Таким образом, в системе (9) оставляем только первые два уравнения и приходим к системе
, а потому является базисным минором. В системе (9) оставим только те уравнения, коэффициенты которых участвуют в образовании базисного минора. Таким образом, в системе (9) оставляем только первые два уравнения и приходим к системе .
. в правую часть и рассмотрим полученную систему
в правую часть и рассмотрим полученную систему
 и
и  при произвольном значении переменной
при произвольном значении переменной  ,
,  ,
, . Поскольку z может быть любым числом, то и t тоже может принимать любые числовые значения. Выражая
. Поскольку z может быть любым числом, то и t тоже может принимать любые числовые значения. Выражая  и подставляя в (11), получим общее решение исходной системы (9) в следующем симметричном виде:
и подставляя в (11), получим общее решение исходной системы (9) в следующем симметричном виде: ,
,  .
. получим нулевое решение системы
получим нулевое решение системы  ). Обратно, любое решение однородной системы получается из приведенных формул (12) при некотором значении параметра t.
). Обратно, любое решение однородной системы получается из приведенных формул (12) при некотором значении параметра t. .
. ,
,  ,
,  ,
,  .
. ,
,  ,
, 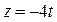 ,
,  или
или  , откуда
, откуда  . Итак, нужное нам решение получается из общего решения при
. Итак, нужное нам решение получается из общего решения при  ,
, 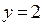 ,
, 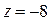 .
. .
.


