
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение линии на плоскостиСодержание книги
Поиск на нашем сайте
В предыдущих параграфах для вектора было введено понятие координат, что позволило значительно упростить действия над векторами, сводя их к обычным арифметическим действиям с числами. Координаты вектора полностью определяли его основные характеристики (длина, направления) и позволяли определять характер взаимного расположения векторов (параллельность, перпендикулярность). Нельзя ли полностью характеризовать каким-либо набором чисел и более сложные (чем вектор) геометрические объекты. Сейчас мы начнем изучать различные кривые, расположенные в некоторой плоскости, и этот вопрос будет актуален.
 (см. рисунок). Нельзя ли ее положение полностью задать каким-либо набором чисел (как для вектора)? Помня, что таковыми могут быть координаты (по опыту векторов), сделаем упомянутую плоскость координатной, тем более, что процедура превращения простой плоскости в координатную весьма проста и заключается в помещении на эту плоскость прямоугольной системы координат, состоящей из двух взаимно перпендикулярных числовых осей. Теперь каждая точка плоскости стала координатной, т.е. получила два числа (см. рисунок). Нельзя ли ее положение полностью задать каким-либо набором чисел (как для вектора)? Помня, что таковыми могут быть координаты (по опыту векторов), сделаем упомянутую плоскость координатной, тем более, что процедура превращения простой плоскости в координатную весьма проста и заключается в помещении на эту плоскость прямоугольной системы координат, состоящей из двух взаимно перпендикулярных числовых осей. Теперь каждая точка плоскости стала координатной, т.е. получила два числа  и и  в качестве своих координат, которые полностью определяют положение точки на плоскости. В частности, положение любой точки рассматриваемой кривой тоже определяется ее координатами. Поэтому если мы зададим таблицей координаты всех точек кривой, то эта числовая таблица однозначно определит положение всей кривой в качестве своих координат, которые полностью определяют положение точки на плоскости. В частности, положение любой точки рассматриваемой кривой тоже определяется ее координатами. Поэтому если мы зададим таблицей координаты всех точек кривой, то эта числовая таблица однозначно определит положение всей кривой  на плоскости. У этой идеи (задавать положение кривой таблицей, содержащей координаты всех ее точек) есть много недостатков, но принципиальный недостаток состоит в том, что точек на кривой бесконечно много, а потому рисование подобной таблицы займет бесконечно много времени. Поэтому от идеи задавать такие сложные геометрические объекты (как кривые) набором чисел придется отказаться. Попробуем другую идею. Для того, чтобы определить положение кривой на плоскости, нам достаточно научиться каким-либо образом узнавать для произвольной точки плоскости лежит ли она на данной кривой или нет. Каков же может быть механизм такого узнавания? Каждая точка характеризуется парой своих координат. Поэтому такой механизм должен, обработав пару чисел на плоскости. У этой идеи (задавать положение кривой таблицей, содержащей координаты всех ее точек) есть много недостатков, но принципиальный недостаток состоит в том, что точек на кривой бесконечно много, а потому рисование подобной таблицы займет бесконечно много времени. Поэтому от идеи задавать такие сложные геометрические объекты (как кривые) набором чисел придется отказаться. Попробуем другую идею. Для того, чтобы определить положение кривой на плоскости, нам достаточно научиться каким-либо образом узнавать для произвольной точки плоскости лежит ли она на данной кривой или нет. Каков же может быть механизм такого узнавания? Каждая точка характеризуется парой своих координат. Поэтому такой механизм должен, обработав пару чисел  и и  (координаты точки), сделать вывод о принадлежности (или непринадлежности) точки данной кривой. А какой обработке можно подвергнуть пару чисел? Пару чисел можно, например, подставить в какую-нибудь формулу и посчитать после этого получающееся по этой формуле число. Тогда возникает следующая идея. Нельзя ли для данной кривой (координаты точки), сделать вывод о принадлежности (или непринадлежности) точки данной кривой. А какой обработке можно подвергнуть пару чисел? Пару чисел можно, например, подставить в какую-нибудь формулу и посчитать после этого получающееся по этой формуле число. Тогда возникает следующая идея. Нельзя ли для данной кривой  подобрать пару таких формул, содержащих две переменные подобрать пару таких формул, содержащих две переменные  и и  (обозначим эти формулы (обозначим эти формулы 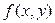 и и  ), которые бы обладали следующим свойством: если в эти формулы подставить координаты любой точки, лежащей на линии ), которые бы обладали следующим свойством: если в эти формулы подставить координаты любой точки, лежащей на линии  , то после вычислений по ним получаются одинаковые числа, а если точка не лежит на , то после вычислений по ним получаются одинаковые числа, а если точка не лежит на  − то разные числа. В этом случае соотношение − то разные числа. В этом случае соотношение  и представляет собой механизм, определяющий принадлежность или непринадлежность точки данной кривой: если при подстановке координат произвольной точки в это соотношение получится верное равенство, то точка лежит на кривой, а нет – так нет. и представляет собой механизм, определяющий принадлежность или непринадлежность точки данной кривой: если при подстановке координат произвольной точки в это соотношение получится верное равенство, то точка лежит на кривой, а нет – так нет.Выражение вида (1) называется уравнением этой линии Замечание. Если в (1) перенести все в левую часть и обозначить получившуюся в этой части формулу через Исследуем вид уравнения (1) для линий различной формы, начиная с простейшей – прямой линии.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.129.8 (0.005 с.) |

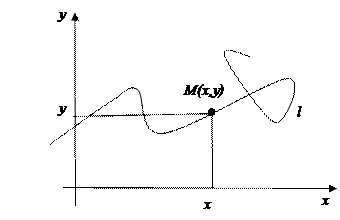

 (т.е.
(т.е.  ), то уравнение линии можно представить в более простой с виду форме:
), то уравнение линии можно представить в более простой с виду форме: 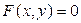 . Именно в такой форме соотношение (1) часто называют уравнением кривой. Однако для дальнейшего изложения более удобным мне кажется соотношение (1).
. Именно в такой форме соотношение (1) часто называют уравнением кривой. Однако для дальнейшего изложения более удобным мне кажется соотношение (1).


