
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории поверхностей второго порядкаСодержание книги
Поиск на нашем сайте
Эти поверхности "похожи" на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Пусть в пространстве задана прямоугольная декартова система координат. По аналогии с кривой второго порядка, поверхностью второго порядка называется поверхность, определяемая уравнением, содержащем квадраты координат:
Далее укажем канонические уравнения основных таких поверхностей. 1. Сфера с центром в точке (1) Пример. Изобразить поверхность с уравнением
2. Эллипсоид имеет каноническое уравнение вида
3. Гиперболоиды бывают однополостными и двуполостными. Однополостный гиперболоид имеет каноническое уравнение вида
где Исследовать форму однополостного гиперболоида можно как и для эллипсоида, определяя форму сечения его плоскостями, параллельными координатным. Получим то, что изображено на левом рисунке. Правый рисунок дает объемное изображение однополостного гиперболоида.
Двуполостный гиперболоид имеет каноническое уравнение вида
4. Конус (второго порядка) имеет каноническое уравнение вида
Где
Если в уравнении конуса 5. Параболоиды бывают эллиптические и гиперболические. Эллиптический параболоид имеет каноническое уравнение вида
где Исследуя привычными методами форму эллиптического параболоида, получим следующие рисунки.
Если в уравнении эллиптического параболоида Гиперболический параболоид имеет каноническое уравнение вида
Каноническое уравнение эллиптического цилиндра имеет вид
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.201.169 (0.01 с.) |

 .
. в этом уравнении? Оказывается, что получающиеся поверхности второго порядка (за исключением случаев сильного вырождения) можно разделить на пять классов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует (подходящая) система координат, в которой поверхность задается наиболее простым уравнением, называемым каноническим уравнением.
в этом уравнении? Оказывается, что получающиеся поверхности второго порядка (за исключением случаев сильного вырождения) можно разделить на пять классов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует (подходящая) система координат, в которой поверхность задается наиболее простым уравнением, называемым каноническим уравнением. радиуса
радиуса  в любой (а не только в подходящей) декартовой прямоугольной системе координат имеет уравнение
в любой (а не только в подходящей) декартовой прямоугольной системе координат имеет уравнение .
. .
. Решение. Группируя слагаемые с
Решение. Группируя слагаемые с  ,
,  ,
, 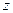 и дополняя их до полных квадратов, получим
и дополняя их до полных квадратов, получим  . Сравнивая с общим видом поверхности сферы (1), получаем, что данная поверхность есть сфера с центром
. Сравнивая с общим видом поверхности сферы (1), получаем, что данная поверхность есть сфера с центром 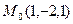 радиуса 2 (см. рисунок).
радиуса 2 (см. рисунок).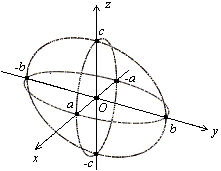
 ,
, где
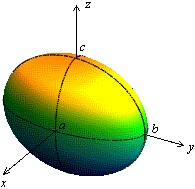
где 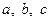 − положительные числа. Очевидно, что в сечении эллипсоида координатными плоскостями
− положительные числа. Очевидно, что в сечении эллипсоида координатными плоскостями  получаются эллипсы с соответствующими полуосями (см. рисунок). Если проводить сечения эллипсоида плоскостями, параллельными координатной плоскости, например,
получаются эллипсы с соответствующими полуосями (см. рисунок). Если проводить сечения эллипсоида плоскостями, параллельными координатной плоскости, например,  , то можно показать, что весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости
, то можно показать, что весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости  , и подобных эллипсу в самой плоскости
, и подобных эллипсу в самой плоскости 


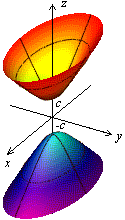





 , то сечения конуса плоскостями, параллельными плоскости
, то сечения конуса плоскостями, параллельными плоскости 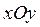 , являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости
, являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости  , вокруг оси
, вокруг оси  . Именно такой конус изучается в школьном курсе математики.
. Именно такой конус изучается в школьном курсе математики.
 и
и  − положительные числа.
− положительные числа.


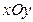 , являются окружностями. В этом случае поверхность называется параболоидом вращения (правый рисунок выше) и может быть образована вращением параболы, лежащей в плоскости
, являются окружностями. В этом случае поверхность называется параболоидом вращения (правый рисунок выше) и может быть образована вращением параболы, лежащей в плоскости  , вокруг оси
, вокруг оси 
 где
где 
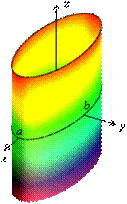
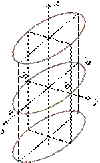 6. Цилиндрической поверхностью называется геометрическое место параллельных между собой прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые − образующими. Несложно показать, что уравнение вида
6. Цилиндрической поверхностью называется геометрическое место параллельных между собой прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые − образующими. Несложно показать, что уравнение вида  определяет цилиндрическую поверхность с образующими, параллельными оси
определяет цилиндрическую поверхность с образующими, параллельными оси  , где
, где 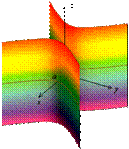 числа.
числа.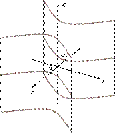 Каноническое уравнение гиперболического цилиндра имеет вид
Каноническое уравнение гиперболического цилиндра имеет вид  , где
, где 

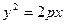 (см. рисунок).
(см. рисунок).


