
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический метод решения задачи линейногоСодержание книги Поиск на нашем сайте
программирования (случай n переменных) Задачу линейного программирования можно свести к задаче, решаемой графическим методом, если она задана в канонической форме, либо после приведения ее к канонической форме, и разность между количеством переменных n и количеством неизвестных m равна двум. В этом случае существует возможность выразить m базисных неизвестных через 2 оставшиеся свободные и, учитывая неотрицательность переменных, перейти от системы уравнений к системе неравенств с двумя неизвестными. Иными словами это означает, что в семействе векторов с координатами, состоящими из коэффициентов при соответствующих переменных, необходимо выделить базис или найти общее решение системы. Проиллюстрируем применение этого метода на примере. Пример. Найдите план, минимизирующий значение функции
Данную задачу можно решить графическим методом, так как выполняется условие n – m = 2. Действительно, в системе ограничений число неизвестных 5, число уравнений 3. Составим расширенную матрицу системы:
Выберем в качестве базисных переменных х 1, х 2, х 3. Следовательно, первые три столбца матрицы должны представлять собой единичную матрицу. Проведем преобразование методом Гаусса: прибавим ко второй и к третьей строкам первую, умноженную на –1.
Последняя матрица получена прибавлением к третьей строке второй, умноженной на 5. Разделим третью строку на –12.
Для того чтобы первые три столбца образовали единичную матрицу, применим преобразование Гаусса «снизу вверх». Прибавим к первой строке третью, умноженную на –3, а ко второй строке – третью, умноженную на 2.
Последняя матрица получена прибавлением к первой строке второй, умноженной на –2. По преобразованной матрице составим систему уравнений:
Выразим базисные переменные через свободные х 4, х 5.
Учтем, что все переменные неотрицательны, следовательно, правые части уравнений так же больше или равны нулю. Получим систему неравенств с двумя неизвестными.
Используя соотношения системы (2.4), выразим целевую функцию через свободные переменные.
Найдем область решений системы (2.5) графически. Построим прямые и определим полуплоскости – решения каждого неравенства (рис. 2.5).
Построим опорную прямую z = 5; Вектор `с на рис. 2.5 направлен по градиенту целевой функции и указывает направление ее роста, следовательно, в противоположную сторону целевая функция будет убывать. Точка «входа» в ОДР – точка О(0,0), точки «выхода» не существует. Подставим координаты точки «входа» в целевую функцию и получим ее минимальное значение z = - 5. Вычислим значения базисных переменных в точке «входа», учитывая (2.4), их значения равны: х 1 = 2; х 2 = 1; х 3 = 2. Итак, минимальное значение целевой функции z = –5, это значение достигается на оптимальном плане (2; 1; 2; 0; 0). Продолжим рассмотрение практических задач, для решения которых требуется составление математических моделей. Пример. Завод производит три типа (I, II, III) некоторого изделия, используя для этого сырье А и В. На изготовление единицы изделия типа I затрачивается в два раза больше рабочего времени, чем на изготовление единицы изделия типа II и в столько же, сколько на изготовление изделия типа III. Рабочие ресурсы завода эквивалентны ресурсам, необходимым на изготовление 1500 шт. изделия типа I. Данные о расходе материалов приведены в таблице. Руководство завода приняло решение ликвидировать склад для хранения сырья А и стремится организовать производство таким образом, чтобы, израсходовав сырье А, полностью получить наибольший доход. Каков должен быть план производства?
Составим математическую модель задачи. 1. Критерием эффективности является доход от производства, стремящийся к максимуму. 2. Параметрами управления являются х 1 – количество изделий типа; х 2 – количество изделий типа II; х 3 – количество изделий типа III. 3. Составим систему ограничений: ограниченными являются ресурсы времени и запасы сырья А и В. Пусть а – затраты времени на производство одного изделия I, тогда 0,5 а - затраты времени на производство одного изделия II, следовательно,
В связи с тем, что сырье А необходимо израсходовать полностью, ограничение на его запас имеет вид:
Ограничение на запас сырья В имеет вид:
4. Целевая функция – доход 5. Выберем метод решения задачи оптимизации по виду математической модели:
Приведем задачу линейного программирования к каноническому виду.
Переменные х 4 играет роль остатка сырья В, а х 5 – роль оставшегося рабочего времени. Число неизвестных системы на два больше числа уравнений, следовательно, задача может быть решена графически. Запишем матрицу системы и выберем базисные переменные.
В качестве базисных удобно выбрать переменные х 1, х 4, х 5. Преобразуем матрицу, разделив первую строку на 2.
Последняя матрица получена прибавлением к третьей строке первой, умноженной на –1, и ко второй – первой, умноженной на –4. По равносильной расширенной матрице системы составим систему уравнений.
Найдем общее решение системы. Выразим базисные переменные через свободные:
Учитывая неотрицательность левых частей уравнений, можем перейти к системе неравенств с двумя неизвестными.
Подставим в целевую функцию выражения (3.6):
Решим получившуюся задачу графически. Построим ОДР системы (2.7). Проведем опорную прямую L, приравняв F = 60000. Ее уравнение после преобразований х 2 + х 3 = 0, grad F = (- 25; - 25). Все построения приведены на рис. 3.6.
F = - 25´500 + 60000 = 47500. Подставим значения переменных в (2.6), получим х 1 = 750, х 4 = 0; х 5 = 0. Итак, для получения наибольшего дохода в количестве 47500 д.е. при заданных условиях необходимо производить 750 ед. продукции типа I, 500 ед. продукции типа II и не производить продукцию типа III, при этом все ресурсы и сырьевые и временные будут израсходованы полностью.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.141.244 (0.006 с.) |

 , при заданных ограничениях хi ³0, i =1, 2,…,5:
, при заданных ограничениях хi ³0, i =1, 2,…,5:
 .
. Þ
Þ  .
. .
. Þ
Þ  .
.
 (2.4)
(2.4)
 (2.5)
(2.5) ,
, .
.


 и, следовательно,
и, следовательно, .
. .
.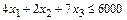 .
. стремится к максимуму на системе ограничений.
стремится к максимуму на системе ограничений.

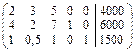 .
. Þ
Þ  .
.
 (2.6)
(2.6)
 (2.7)
(2.7)
 В выделенном многоугольнике решений точкой «выхода» в направлении вектора-градиента целевой функции является точка с координатами х 2 = 500, х 3=0. Значение целевой функции в этой точке:
В выделенном многоугольнике решений точкой «выхода» в направлении вектора-градиента целевой функции является точка с координатами х 2 = 500, х 3=0. Значение целевой функции в этой точке:


