
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные задачи дискретного программирования.Содержание книги Поиск на нашем сайте
Транспортная задача Основные задачи дискретного программирования Дискретное программирование – область математики, занимающаяся исследованием и решением экстремальных задач на конечных множествах. Пусть множество векторов М = { a 1, a 2,…, an }, требуется найти элемент х = aj ÎM, на котором достигается абсолютный максимум (или абсолютный минимум) функции W на М:
Дискретное программирование исследует только те задачи, где число элементов, входящих в множество М, достаточно велико, и решение не может быть найдено простым перебором. Универсальных методов решения задач дискретного программирования не создано. Но исследованы узкие классы задач, такие как: транспортная задача, линейное целочисленное программирование, задача о расписаниях, экстремальные задачи на графах. Во-первых, двух из перечисленных задач дискретного программирования математические модели можно считать моделями задач линейного программирования, однако для нахождения оптимального значения используют свои специальные методы. Рассмотрим это на примере так называемой транспортной задачи. Транспортная задача На базах Б1, Б2,..., Бm сосредоточены однородные ресурсы в количествах b1,b2,...,bm соответственно. Указанные ресурсы должны быть доставлены потребителю на объекты П1,П2,...,Пn в количествах а 1, а 2,..., а n соответственно, причем сумма всех заявок потребителей равна сумме всех запасов на базах, то есть
Известны затраты Cij на доставку единицы ресурса с любой базы Б i на любой объект П j. Требуется составить такой план доставки ресурсов с баз на объекты, при котором общая сумма всех затрат на перевозки (расход топлива, моторесурса, пробег, время и т.п.) была бы наименьшей ивсе потребности потребителей были бы выполнены. Условие равенства запасов и потребностей носит название закрытой транспортной задачи. Методами дискретного программирования решаются только «закрытые» задачи. В случае если задача «открыта» ее сводят к «закрытой»: а) в случае дефицита вводят дополнительную базу Б m +1 на которой располагают необходимый объем товара. Ресурс, отвезенный с этой «мнимой» базы по нулевой цене, показывает, сколько товара недополучит каждый потребитель. б) в случае перепроизводства вводят дополнительного «фиктивного потребителя», чьи потребности соответствуют излишку на базах. Ресурс, отвезенный этому потребителю с i -ой базы по нулевой цене, интерпретируется как остаток на этой базе.
Составим математическую модель задачи: 1. Критерием эффективности поставленной задачи будут общие затраты на перевозки. 2. Параметры условия удобно поместить в таблицу, называемую транспортной таблицей. Ячейки поля таблицы разделены на две части. В верхней указывается стоимость перевозки единицы груза с конкретной базы конкретному потребителю, а в нижней – количество перевезенного груза.
3. Параметрами условия являются объемы ресурса, отвезенные с каждой базы каждому потребителю. Их количество m ´ n. Для удобства их нумеруют не одним индексом, а двумя, так x ij – количество груза, отвезенное с i -ой базы j -ому потребителю. 4. Предположим, что транспортная задача является закрытой или сведена к ней. Тогда в задаче существуют следующие ограничения: суммарное количество груза, направляемое из каждой базы всем потребителям, должно быть равно запасу груза на данной базе, т.е.
Суммарное количество груза, доставляемое каждому потребителю со всех баз, должно быть равно заявке, поданной данным потребителем, т.е.
Все параметры управления неотрицательны x ij ³ 0. Систему ограничений называют балансовыми условиями, онасостоит из n + m уравнений, однако если сложить все уравнения системы (2.9) и все уравнения системы (2.10), то получим одинаковые уравнения, следовательно, система уравнений зависима, поэтому можно удалить одно из уравнений системы. В итоге система ограничений будет содержать n + m – 1 линейно независимых уравнений, следовательно, базисных переменных также будет n + m – 1. И в базисном решении не более n + m – 1 переменной отличной от нуля. 5. Целевая функция – общие затраты на перевозку, выражается через параметры управления по следующей формуле
Требуется найти решение, минимизирующее целевую функцию в области допустимых решений систем (2.9) и (2.10).
Целевая функция и система ограничений линейны, следовательно, транспортную задачу можно рассматривать как задачу линейного программирования, однако на нее наложено дополнительное условие: все параметры управления должны быть целыми, поэтому область допустимых решений является конечным множеством, хотя и с очень большим количеством элементов. Прежде чем описать алгоритм решения транспортной задачи введем определения: любое решение системы ограничений называется допустимым планом. Допустимый план называют опорным, если это решение системы является базисным, и в нем отличны от нуля n +m –1 переменная. Если хотя бы одна базисная переменная станет равной нулю, т.е. план будет включать в себя меньше чем m + n – 1 положительных переменных, то он называется вырожденным. Решение транспортной задачи в общем случае сводится к преобразованию транспортной таблицы, поэтому будем называть клетку, стоящую в i -й строке, j -м столбце, – клетка (i, j). Клетки, в которых записаны базисные переменные, будем называть «занятыми», а остальные «свободными». Свободные переменные в таблицу не записывают. Представим алгоритм решения транспортной задачи в виде блок-схемы:
Нет Да
Покажем использование этого алгоритма на примере конкретной задачи. На трех базах снабжения горючим Б1, Б2, Б3 имеется соответственно 40, 60 и 60 т топлива, которое необходимо доставить на четыре бензозаправочные станции П1, П2, П3, П4 в количествах 40, 40, 30 и 50т соответственно. Затраты (стоимости) перевозки тонны горючего с базы Б1 на станции П1, П2, П3, П4 составляют соответственно 3, 1, 5 и 4 денежных единиц, с базы Б2 – 6, 1, 2 и 2 денежных единиц, с базы Б3 – 4, 4, 5 и 5 денежных единиц (стоимость перевозки можно оценить, например, стоимостью расходуемого при перевозке топлива). Составить такой план доставки топлива с баз на бензозаправочные станции, при котором общая сумма затрат была бы наименьшей. I. Модель задачи закрытая, так как
II. На основании исходных данных составим транспортную таблицу. Таблица состоит из m = 3 строк (количество баз) и n = 4 столбцов (количество потребителей).
III. Составим первый опорный план. Существует несколько методов построения первого опорного плана. Наиболее употребляемые из них это метод северо-западного угла и метод наименьшей стоимости. Построим опорный план задачи методом “северо-западного угла”. Метод северо-западного угла (диагональный метод). При этом методе первая базисная переменная х 11 (верхняя левая (северо-западная) клетка таблицы). Ей присваивается максимально допустимое значение количества груза; затем базисной выбирается, соседняя клетка (в строке или столбце в зависимости от того, где имеются еще неиспользованные возможности перевозок); таким же образом (вправо и вниз) производится дальнейшее заполнение клеток до распределения всего количества груза. Если ни в ту, ни в другую из соседних клеток ничего поставить нельзя (то есть возможности соответствующих строки и столбца уже исчерпаны), то следующая базисная переменная, соответствующая любой из этих клеток, берется равной нулю, и от нее продолжается процесс последовательного распределения, этот прием гарантирует получение в исходном плане необходимого количества занятых клеток (m+n –1). План получается вырожденным, но это не мешает обычному порядку расчета. Клетка с нулевой поставкой в процессе вычисления считается занятой.
На базе Б1 имеется 40 единиц груза. Выделим их потребителю П1 (запишем в клетку (1,1) – первая строка, первый столбец, число 40). Запасы первой базы и первого потребителя одновременно исчерпаны, следовательно, следующая базисная переменная соответствует клетке либо (2,1), либо (1,2) и равна нулю. Пусть базисной будет переменная х 12=0. На базе Б2 находится 60 единиц груза; выделим 40 единиц груза потребителю П2 и оставшиеся 20 единиц потребителю П3. Недостающие 30 – 20 = 10 единиц груза выделим П3 с базы Б3. На базе Б3 осталось 60 – 10 = 50 единиц груза; выделим их потребителю П4 (принцип распределения: сначала распределяем все, что имеется на данной базе и лишь затем переходим к следующей).
Составили первый план. Проверим, является ли этот план допустимым (все заявки должны быть удовлетворены, все запасы исчерпаны), то есть суммы поставок по строкам должны быть равны запасам на базах, а по столбцам – запросам потребителей. Проверим, является ли полученный план опорным. Количество базисных переменных, а, следовательно, заполненных клеток должно быть m + n –1= 3+4–1=6. IV. Проверим план на оптимальность, то есть будет ли при этом плане общая сумма денежных затрат на перевозку минимальной, или ее можно еще уменьшить путем изменения плана перевозок. Для исследования полученного плана на оптимальность используют метод, называемый «методом потенциалов». Он состоит из двух этапов: 1. К таблице добавляют строку и столбец, в которых записывают числа (потенциалы) по строкам U i и по столбцам V j. Эти числа подбирают так, чтобы для занятых клеток выполнялось равенство: U i + V j + Cij=0. (2.11) 2. Вычисляют «оценки» перевозок в клетках по формуле: C/ ij =U i +V j +C ij, (2.12) где C / ij – оценка перевозки в клетке (i,j). Если в результате пересчета появились клетки с отрицательными оценками (C /ij < 0), то построенный план неоптимальный, и его можно улучшить за счет выбора в качестве базисной переменной, соответствующей клетке с отрицательной оценкой. Если таких клеток несколько, то наиболее “выгодной” клеткой будет клетка с наибольшей по абсолютной величине отрицательной оценкой.
Проверим на оптимальность полученный план в нашей задаче. Для этого достроим в предыдущей таблице строку и столбец для потенциалов. Для занятой клетки (1,1) (первая строка, первый столбец) возьмем произвольно V1 = 0. Для занятой клетки должно выполнятся равенство U1+V1+C11=0, следовательно U1+0+3=0, отсюда U1= –3. Для занятой клетки (1;2) (вторая строка, первый столбец) имеем U1= –3, тогда V2–3+1=0, отсюда V2=2. Для занятой клеткой (2,2) имеем V2=2, тогда U2+2–1=0, получим U2= –3. Для занятой клетки (2;3) имеем U2= –3, тогда –3+V3+2=0, получим V3 = 1. Для клетки (3,3) V3=1, тогда U3+1+5=0, отсюда U3= –6 и для клетки (3,4) имеем –6+V4+5=0, получим V4=1. Сделаем оценки перевозок для клеток и построим новую таблицу. Для занятых клеток оценки будут равны нулю, а для свободных клеток вычисляется по формуле (2.12) Для клетки (1;3) оценка будет С /13 = –3+1+5 = 3. Для клетки (1;4): С /14 = –3+1+4 = 2. Для клетки (2,1): С /21 = –3+0+6=3. Для клетки (2;4): С /24 = –3+1+2 = 0. Для клетки (3;1): С /31 = –6+0+4 = –2. Для клетки (3;2): С /32 = –6+2+4 = 0. Составим таблицу с учетом пересчета стоимостей:
Замечание. После занесения оценок в таблицу для их обозначения опять используем символ Сij. В полученной таблице имеется клетка с отрицательной оценкой, это клетка (3,1) со стоимостью С31= –2, следовательно, план не оптимальный. В нее и будем перебрасывать груз. V. Улучшение плана. Переброска груза в “выгодную” клетку (изменение базисного решения) возможна только при условии сохранения суммы перевозок по строкам и столбцам. Цикл – это замкнутый многоугольник с горизонтальными и вертикальными сторонами, одна вершина которого лежит в данной свободной клетке, а остальные – в занятых (базисных) клетках. В теории линейного программирования доказывается, что если составленный план – опорный, то для каждой свободной клетки транспортной таблицы существует и при том единственный цикл.
Выберем наименьшее количество груза в клетках с маркером минус: min {40; 40; 10} = 10, в клетке (3,3). Новое базисное решение стоится следующим образом: вместо переменной х33 базисной становится переменная х31, ее значение становится равным 10. Значения базисных переменных, помеченных знаком (+), увеличивается на 10, а, помеченных знаком (–) уменьшается на 10. Если базисная переменная не входила в цикл, то ее значение не изменяется. Составим новую таблицу с учетом выполненной переброски груза:
VI. Проверка плана на оптимальность (повторение IV шага):
1. Вычислим значения потенциалов по значениям оценок в предыдущей таблице по формуле (3.11): Для занятой клетки (1,1) возьмем произвольно V1 = 0, следовательно, U1=0. Для занятой клетки (1;2) имеем U1= 0,тогда V2=0. Для занятой клеткой (2,2) имеем V2= 0, тогда U2=0. Для занятой клетки (2;3) имеем U2=0, тогда V3=0. Для клетки (3,1) V1=0, тогда U3 -2=0, отсюда U3=2 и для клетки (3,4) имеем 2+V4+0=0, получим V4= –2. Сделаем оценки перевозок для клеток и построим новую таблицу. Для занятых клеток оценки будут равны нулю, а для свободных клеток вычисляется по формуле (3.12) Для клетки (1;3) оценка будет С /13 = 0+0+3 = 3. Для клетки (1;4): С /14 = 2–2+0 = 0. Для клетки (2,1): С /21 = 0+0+3=3. Для клетки (2;4): С /24 = 0–2+0 = –2. Для клетки (3;2): С /32 = 2+0+0 = 2. Для клетки (3;3): С /33 = 2+0+0 = 2. Среди оценок есть отрицательная, следовательно, план не оптимальный. Составим таблицу с учетом пересчета стоимостей:
Найдем цикл для клетки (2,4) и отметим его контуром в предыдущей таблице. Нарисуем этот цикл отдельно, минимальное значение в клетках, помеченных маркером «–» равно 30. Это число встречается дважды, следовательно, после переброски по циклу 30 единиц, в двух клетках (1,1) и (2,3) появится нулевые значения. Это означает, что одна из базисных переменных станет равной нулю, хотя и останется базисной. Для определенности, пусть базисная переменная х24 войдет в базис вместо переменной х11 (а переменная х 23 останется базисной). Тогда составим новую таблицу с учетом изменения базисного решения.
VIII. Проверка плана на оптимальность (повторение IV шага): Методом потенциалов проверим получившийся план на оптимальность, занесем потенциалы, вычисленные по (3.11) в предыдущую таблицу. Переоценим стоимости по (3.12) и составим новую таблицу: Все оценки неотрицательны, следовательно, получившийся план оптимальный. Итак, с базы Б1 будем перевозить все 40 тонн на станцию П2 с базы Б2 – 30 тонн на станцию П3 и 30 тонн на станцию П4; с базы Б3 – 40 тонн на станцию П1 и 30 тонн на станцию П4. Подсчитаем стоимость перевозки по найденному плану. Значения стоимостей перевозки одной тонны возьмем из условия задачи. W=1 Для сравнения можем вычислить стоимость опорного плана: W=3 Как и следовало ожидать, значение целевой функции уменьшилось.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.66.35 (0.013 с.) |

 или
или 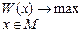 .
. .
. (2.9)
(2.9) (2.10)
(2.10)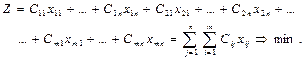

 .
. 0
0
 Найдем цикл для клетки (3,1) и отметим его контуром в предыдущей таблице. Нарисуем этот цикл отдельно, указав в нем количество груза в заполненных клетках. Припишем вершине свободной клетки знак (+), следующей знак (–) и далее чередуем знаки вершин многоугольника. Знак плюс (+) указывает, что в эти клетки будем перебрасывать груз; знак минус (–), что из этих клеток будем брать груз для переброски. Число единиц груза, которые можно перебросить по циклу определяется наименьшей перевозкой, стоящей в клетке со знаком минус (–).
Найдем цикл для клетки (3,1) и отметим его контуром в предыдущей таблице. Нарисуем этот цикл отдельно, указав в нем количество груза в заполненных клетках. Припишем вершине свободной клетки знак (+), следующей знак (–) и далее чередуем знаки вершин многоугольника. Знак плюс (+) указывает, что в эти клетки будем перебрасывать груз; знак минус (–), что из этих клеток будем брать груз для переброски. Число единиц груза, которые можно перебросить по циклу определяется наименьшей перевозкой, стоящей в клетке со знаком минус (–). 0
0
 VII. Улучшение плана (повторение V шага).
VII. Улучшение плана (повторение V шага). 40+2
40+2 


