
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2 Линейные методы оптимального управленияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Глава 2 Линейные методы оптимального управления § 2.1. Математические оптимизационные модели. Общая постановка задачи линейного программирования. Графический метод решения задачи линейного Программирования
Математические оптимизационные модели.
Современная экономическая теория включает в себя как необходимый элемент исследования метод математического моделирования. Математической моделью объекта или явления называется его отображение в виде совокупности разного рода уравнений, неравенств, логических отношений, графиков. Использование математики позволяет выделить и формально описать наиболее важные, существенные связи экономических переменных и объектов и получить из них новые знания об объекте, используя абстрактные математические методы исследования. Существуют различные типы моделей. Оптимизационные модели – модели, преследующие цель выбора наименьшего или наибольшего значения некоторого критерия при условии выполнения системы ограничений. Подобные микромодели могут использоваться в теории управления, для обоснования принятия того или иного решения. В следующих параграфах мы будем изучать оптимизационные математические модели. Раздел математики, занимающийся методами оптимизации, называется теорией оптимального управления. Она включает в себя такие подразделы как линейное программирование, нелинейное программирование, динамическое программирование и другие. Основные этапы построения оптимизационной математической модели на примере линейных методов можно представить следующим образом. Этап. Выбор критерия эффективности. Целью задачи является принятие решения, при котором некоторый параметр примет наибольшее или наименьшее значение. Функция, которая выражает значение этого параметра, является критерием эффективности принятого решения и называется целевой функцией. Например, критерием эффективности некоторого предприятия может служить прибыль, стремящаяся принять наибольшее значение, или расходы на организацию предприятия, которые должны быть минимальными. Этап. Определение параметров условия. Параметры условия – постоянные величины, значение которых нельзя изменить в условиях данной задачи. Этап. Выбор параметров управления. Переменные величины, изменяя значения которых, можно изменить значение критерия эффективности, называют параметрами управлениия. Набор параметров управления называют планом. Всякий набор значений переменных х1 , х2 ,..., хn удовлетворяющий системеограничений, называют допустимым планом. Тот допустимый план, при котором целевая функция принимает максимальное (или минимальное) значение, называют оптимальным планом (стратегией, управлением). Этап. Составление системы ограничений. Система ограничений - совокупности соотношений (уравнений или неравенств), которые связывают параметры управления и параметры условия. Симплексный метод решения задачи Линейного программирования
Решение общей задачи линейного программирования геометрическим методом наглядно в специальных случаях. В случае большего числа переменных используют универсальный метод, называемый симплекс-методом. Отметим без доказательства, по аналогии со случаем двух переменных следующее: областью допустимых решений задачи линейного программирования является в случае двух переменных выпуклый многоугольник, в случай трех переменных - выпуклый многогранник, в случае n переменных – выпуклый n -мерный многогранник. Причем координатами его угловых точек являются базисные решения системы ограничений. При этом оптимальное решение, если оно существует, обязательно достигается в некоторой вершине многогранника. В двухмерном случае критерием выбора нужной угловой точки является опорная прямая, хотя можно было бы перебрать все координаты всех угловых точек. Аналогично симплексный метод позволяет осуществить упорядоченный перебор вершин. В основе его лежит алгоритм симплексного преобразования системы, обеспечивающий переход не к любому, а к лучшему решению. При этом, учитывая, что число базисных решений конечно, можно сформулировать теорему: если на каждом шаге симплекс-метода получается невырожденный опорный план, то через конечное число шагов будет получен оптимальный план, или доказано, что он не существует. Выделим основные этапы решения задачи линейного программирования с помощью симплекс-метода. 1. Приведение задачи к каноническому виду. 2. Нахождение некоторого опорного базисного решения. 3. Проверка полученного опорного плана на оптимальность. 4. В случае неоптимальности опорного плана происходит переход к новому базисному решению, уменьшающему (или увеличивающему) значение целевой функции. Выбор базисных решений происходит путем преобразования системы уравнений методом Гаусса. Для наглядности преобразований поместим расширенную матрицу системы ограничений в таблицу. Для построения симплекс таблицы необходимо предварительно преобразовать систему таким образом, что бы в ней были выделены базисные переменные по правилу: если какая-нибудь переменная входит в систему ограничений только в одно из уравнений, имея тот же знак, что и свободный член правой части, то эту переменную можно принять за базисную. Для задачи вида: F =
Симплексная таблица выглядит следующим образом:
Вторая сточка и второй столбец являются заголовками: в строчке перечисляются все неизвестные, а в столбце те из них, которые образуют базисное решение (xk, xl,…,xm). В первой строчке и первом столбце записываются коэффициенты целевой функции при соответствующих переменных. Последняя строка является вспомогательной и используется для полученных позже оценок оптимальности плана. Во все остальные строчки и столбцы записывается расширенная матрица системы. Не нарушая общности рассуждений, рассмотрим симплекс-метод на конкретном примере. Пример. Четыре изделия В1, В2, В3, В4 последовательно обрабатываются на двух станках. Данные, описывающие этот технологический процесс, приведены в таблице. При каком плане производства суммарная цена изделий будет максимальной?
Составим математическую модель задачи: Критерий эффективности - суммарная цена изделий, параметры управления x 1, x 2, x 3 и x 4 – количества изделий каждого вида. Все переменные должны быть неотрицательны. Ограничения на время работы первого станка:
Ограничения на время работы второго станка:
Целевая функция I шаг. Приведем систему к каноническому виду. Так как левые части неравенств не превышают правые, то добавление неотрицательных переменных x 5; x 6 сведет неравенства к равенствам. Эти переменные играют роль неизрасходованной нагрузки станков. Математическая модель задачи в каноническом виде:
II шаг. Выберем первое опорное базисное решение. Так как система ограничений содержит два неравенства (без учета неотрицательности переменных), то базисных переменных может быть максимум две. По указанному выше правилу в нашем случае такими переменными являются x 5, x 6, так как они входят только в одно из уравнений с коэффициентами, равными единице. Составим первую симплекс таблицу:
Итак, если принять все свободные переменные x 1, x 2, x 3, x 4 равными нулю, то получим первый план (0, 0, 0,0, 500, 380). Обратим внимание, что если коэффициенты при базисных переменных равны 1, то их значения равны свободным членам и, следовательно, записываются в последнем столбце. III шаг. Проверим план на оптимальность. Вычислим оценки D j по правилу Например, D1= 0×2+0×3−30 = –30. Занесем значения оценок в таблицу. Для того, чтобы сделать вывод, руководствуются правилом, если целевая функция стремиться к максимуму, то для оптимального плана все оценки неотрицательны, если же к минимуму, то неположительны. У нас есть отрицательные оценки, следовательно, план неоптимальный. В ячейке на пересечении последнего столбца и последней строки вычисляется значение целевой функции на базисном решении. Z = 0. IV шаг. Перейдем к следующему плану. В качестве новой базисной переменной выбирают одну из тех, чья оценка отрицательна, например, х 2. Столбец, в котором находится новая базисная переменная, называется ключевым. Для определения вместо какой переменной x 5 или x 6 выбирается переменная х 2 выбираем минимум из отношений элементов столбца свободных членов и положительных элементов ключевого столбца.
Такой выбор связан с тем, что формально, неравенства, выражающие неотрицательность переменных, в матрицу системы не вошли. Однако, в связи с тем, что в базисном плане переменные равны свободным членам, то последние не должны быть отрицательны. Выбор (2.8) позволят осуществить преобразование Гаусса так, что столбец свободных членов не будет содержать отрицательных элементов.
Строка с меньшим отношением называется ключевой, в нашем случаепервая. Элемент, стоящий на пересечении ключевой строки и ключевого столбца, называется ключевым (этот элемент выделен в таблице). Преобразуем расширенную матрицу системы так, чтобы базисными переменными стали x 2; x 6. Для этого применим стандартный порядок преобразований. 1) Разделим ключевую строку на ключевой элемент. 2) Получившуюся строку умножаем на число, стоящее в i - ой строке ключевого столбце, но с противоположным знаком и прибавляем к i - ой строке. Это приведет к тому, что в ключевом столбце ключевой элемент станет равным 1, а остальные равными нулю.
Первая строка получена делением на 3 (преобразование 2 рода). Вторая строка получена прибавлением к ней новой первой строки, умноженной на –2 (преобразование 3 рода). Новый план: (0; V шаг. Проверим план на оптимальность, вычислим оценки D j. Например, Значение целевой функции на этом плане:
VI шаг. В первом столбце – отрицательная оценка, следовательно, план неоптимальный. Выбираем этот столбец за ключевой. Составим отношения для выбора ключевой строки.
Следовательно, ключевая строка – вторая. Базисными переменными станут x 1 и x 2. Преобразуем расширенную матрицу системы: разделим ключевую строку на ключевой элемент
Вычислим оценки плана и внесем их в таблицу. Отрицательных оценок нет, следовательно, план (28; 148; 0;0;0;0) оптимальный. Максимальное значение целевой функции 5280. Итак, суммарная цена изделий будет максимальной и равной 5280, если производить 28 изделий В1, 148 изделий В2 и не производить изделия В3, В4. Такой вывод не должен вызывать удивление, так как у нас всего два ограничения, следовательно, только две базисные переменные, поэтому только два параметра могут принимать положительные значения, остальные равны нулю. Рассмотрим пример, в котором определение первого опорного плана не так тривиально. Найдите наибольшее значение функции
Приведем задачу к каноническому виду: к левой части второго неравенства прибавим неотрицательную переменную x 4, чтобы уравнять ее с правой частью, а из левой части третьего неравенства, напротив, вычтем неотрицательную переменную x 5, чтобы также уравнять с правой частью.
По приведенному выше правилу выбрать базисные переменные нельзя, поэтому необходимо преобразовать расширенную матрицу системы методом Гаусса, что бы выделить базисные переменные. Как указывалось выше, не любое базисное решение может быть опорным, а только неотрицательное, поэтому для выбора переменных, входящих в базис, воспользуемся подходом, который определяет формула (2.8). Рассуждения проводятся следующим образом: какой из столбцов можно привести к виду (1; 0; 0) – только второй или третий, так как элементы а 12 и а 13 положительны, выберем из них тот, который соответствует правилу (2.8), то есть минимум отношения свободного члена к соответствующему элементу матрицы был бы в первой строке.
Видим, что это справедливо для обоих столбцов, поэтому любой из них можно выбрать за первый базисный вектор. Решим задачу дважды, сначала выберем второй столбец и преобразуем систему: к третьей строке прибавим первую, умноженную на –1.
В качестве второй базисной переменной выберем x 4, так как столбец уже имеет базисный вид (0; 1; 0). Третьей базисной переменной может быть только x 1, так как в последней строке только один элемент положителен. Проверим, выполняется ли для него правило (2.8).
Минимум соответствует третьей строке, значит, x 1 может быть базисной переменной с неотрицательным значением. Разделим третью строку на 2. Затем вычтем ее из второй строки и прибавим к первой.
Итак, базис (x 2, x 4, x 1). Составим симплексную таблицу и проверим план на оптимальность.
Все оценки неотрицательны, следовательно, сразу получен оптимальный план (2, 4, 0, 4, 0), наибольшее значение целевой функции –2. Напомним, что две последние переменные вспомогательные, следовательно, оптимальное решение (2, 4, 0). Повторим решение системы, взяв за первую базисную переменную - x 3. Преобразуем матрицу, приведя этот столбец к виду (1,0,0). Разделим первую строку на элемент а 13,затем вычтем получившуюся строку из второй и третьей.
В качестве второй базисной переменной можно взять x 4, тогда последнюю базисную переменную нужно выбрать из x 1 или x 2. Составим отношения (2.8) для каждого из этих столбцов:
первый результат соответствует второй строке, а второй результат - первой строке, следовательно, ни первый, ни второй столбец не удастся привести к виду (0, 0, 1) так, чтобы свободные члены остались неотрицательны. Следовательно, предыдущий выбор был ошибочным, за вторую базисную переменную следует взять x 1, так как для первого столбца минимум отношений соответствует второй строке. Приведем первый столбец к виду (0, 1, 0). Разделим вторую строку на 1,5. Затем получившуюся строку, умножив на 0, 5, прибавим к первой и, умножив на –1,5, прибавим к третьей.
За третью базисную переменную необходимо взять x 2. Соотношение (2.8) для второго столбца минимально именно в третьей строке. Прибавим ко второй строке третью, деленную на 3, и к первой строке - третью, деленную на –3.
Итак, выбрали базисные переменные x 3, x 1 и x 2. Первый базисный план
Опорный план не оптимален, так как есть отрицательные оценки. Выберем четвертый столбец за ключевой, составим для него соотношение (2.8).
Ключевая строка – первая. Следовательно, вместо базисной переменной x 3 в базис войдет переменная x 4. Преобразуем четвертый столбец к виду (1; 0; 0). Ключевую строку разделим на ключевой элемент
Второй план (2, 4, 0, 2, 0), проверив его на оптимальность, получаем неотрицательные оценки, следовательно, он оптимален. Мы получили то же решение, только более длинным путем.
Если одна из пары задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение, причем значения целевых функций задач на них совпадают. Если же одна из них не имеет оптимального решения, то у другой система ограничений будет несовместна. По решению двойственной задачи можно восстановить решение исходной задачи. Для этого используют вторую теорему двойственности: Если при подстановке оптимального решения в систему ограничений i- ое ограничение выполняется как строгое неравенство, то i -ая координата оптимального решения двойственной задачи равна нулю, и, наоборот, если i -ая координата оптимального решения двойственной задачи отлична от нуля то, i-ое ограничение исходной задачи выполняется как равенство. Подставим решение (6; 6) в систему ограничений, так как обе координаты отличны от нуля, то в исходной задаче оба ограничения выполняются как равенства
Первые два ограничения выполняются как равенства, вторые два – как строгие неравенства (этот результат виден также из рисунка). По теореме третья и четвертая координаты исходной задачи равны нулю. Подставим получившийся результат в систему ограничений исходной задачи:
Решим систему методом Крамера:
Получили то же оптимальное решение, что и в предыдущем параграфе симплексным методом.
Транспортная задача Транспортная задача На базах Б1, Б2,..., Бm сосредоточены однородные ресурсы в количествах b1,b2,...,bm соответственно. Указанные ресурсы должны быть доставлены потребителю на объекты П1,П2,...,Пn в количествах а 1, а 2,..., а n соответственно, причем сумма всех заявок потребителей равна сумме всех запасов на базах, то есть
Известны затраты Cij на доставку единицы ресурса с любой базы Б i на любой объект П j. Требуется составить такой план доставки ресурсов с баз на объекты, при котором общая сумма всех затрат на перевозки (расход топлива, моторесурса, пробег, время и т.п.) была бы наименьшей ивсе потребности потребителей были бы выполнены. Условие равенства запасов и потребностей носит название закрытой транспортной задачи. Методами дискретного программирования решаются только «закрытые» задачи. В случае если задача «открыта» ее сводят к «закрытой»: а) в случае дефицита вводят дополнительную базу Б m +1 на которой располагают необходимый объем товара. Ресурс, отвезенный с этой «мнимой» базы по нулевой цене, показывает, сколько товара недополучит каждый потребитель. б) в случае перепроизводства вводят дополнительного «фиктивного потребителя», чьи потребности соответствуют излишку на базах. Ресурс, отвезенный этому потребителю с i -ой базы по нулевой цене, интерпретируется как остаток на этой базе.
Составим математическую модель задачи: 1. Критерием эффективности поставленной задачи будут общие затраты на перевозки. 2. Параметры условия удобно поместить в таблицу, называемую транспортной таблицей. Ячейки поля таблицы разделены на две части. В верхней указывается стоимость перевозки единицы груза с конкретной базы конкретному потребителю, а в нижней – количество перевезенного груза.
3. Параметрами условия являются объемы ресурса, отвезенные с каждой базы каждому потребителю. Их количество m ´ n. Для удобства их нумеруют не одним индексом, а двумя, так x ij – количество груза, отвезенное с i -ой базы j -ому потребителю. 4. Предположим, что транспортная задача является закрытой или сведена к ней. Тогда в задаче существуют следующие ограничения: суммарное количество груза, направляемое из каждой базы всем потребителям, должно быть равно запасу груза на данной базе, т.е.
Суммарное количество груза, доставляемое каждому потребителю со всех баз, должно быть равно заявке, поданной данным потребителем, т.е.
Все параметры управления неотрицательны x ij ³ 0. Систему ограничений называют балансовыми условиями, онасостоит из n + m уравнений, однако если сложить все уравнения системы (2.9) и все уравнения системы (2.10), то получим одинаковые уравнения, следовательно, система уравнений зависима, поэтому можно удалить одно из уравнений системы. В итоге система ограничений будет содержать n + m – 1 линейно независимых уравнений, следовательно, базисных переменных также будет n + m – 1. И в базисном решении не более n + m – 1 переменной отличной от нуля. 5. Целевая функция – общие затраты на перевозку, выражается через параметры управления по следующей формуле
Требуется найти решение, минимизирующее целевую функцию в области допустимых решений систем (2.9) и (2.10). Целевая функция и система ограничений линейны, следовательно, транспортную задачу можно рассматривать как задачу линейного программирования, однако на нее наложено дополнительное условие: все параметры управления должны быть целыми, поэтому область допустимых решений является конечным множеством, хотя и с очень большим количеством элементов. Прежде чем описать алгоритм решения транспортной задачи введем определения: любое решение системы ограничений называется допустимым планом. Допустимый план называют опорным, если это решение системы является базисным, и в нем отличны от нуля n +m –1 переменная. Если хотя бы одна базисная переменная станет равной нулю, т.е. план будет включать в себя меньше чем m + n – 1 положительных переменных, то он называется вырожденным. Решение транспортной задачи в общем случае сводится к преобразованию транспортной таблицы, поэтому будем называть клетку, стоящую в i -й строке, j -м столбце, – клетка (i, j). Клетки, в которых записаны базисные переменные, будем называть «занятыми», а остальные «свободными». Свободные переменные в таблицу не записывают. Представим алгоритм решения транспортной задачи в виде блок-схемы:
Нет Да
Покажем использование этого алгоритма на примере конкретной задачи. На трех базах снабжения горючим Б1, Б2, Б3 имеется соответственно 40, 60 и 60 т топлива, которое необходимо доставить на четыре бензозаправочные станции П1, П2, П3, П4 в количествах 40, 40, 30 и 50т соответственно. Затраты (стоимости) перевозки тонны горючего с базы Б1 на станции П1, П2, П3, П4 составляют соответственно 3, 1, 5 и 4 денежных единиц, с базы Б2 – 6, 1, 2 и 2 денежных единиц, с базы Б3 – 4, 4, 5 и 5 денежных единиц (стоимость перевозки можно оценить, например, стоимостью расходуемого при перевозке топлива). Составить такой план доставки топлива с баз на бензозаправочные станции, при котором общая сумма затрат была бы наименьшей. I. Модель задачи закрытая, так как
II. На основании исходных данных составим транспортную таблицу. Таблица состоит из m = 3 строк (количество баз) и n = 4 столбцов (количество потребителей).
III. Составим первый опорный план. Существует несколько методов построения первого опорного плана. Наиболее употребляемые из них это метод северо-западного угла и метод наименьшей стоимости. Построим опорный план задачи методом “северо-западного угла”. Метод северо-западного угла (диагональный метод). При этом методе первая базисная переменная х 11 (верхняя левая (северо-западная) клетка таблицы). Ей присваивается максимально допустимое значение количества груза; затем базисной выбирается, соседняя клетка (в строке или столбце в зависимости от того, где имеются еще неиспользованные возможности перевозок); таким же образом (вправо и вниз) производится дальнейшее заполнение клеток до распределения всего количества груза. Если ни в ту, ни в другую из соседних клеток ничего поставить нельзя (то есть возможности соответствующих строки и столбца уже исчерпаны), то следующая базисная переменная, соответствующая любой из этих клеток, берется равной нулю, и от нее продолжается процесс последовательного распределения, этот прием гарантирует получение в исходном плане необходимого количества занятых клеток (m+n –1). План получается вырожденным, но это не мешает обычному порядку расчета. Клетка с нулевой поставкой в процессе вычисления считается занятой. На базе Б1 имеется 40 единиц груза. Выделим их потребителю П1 (запишем в клетку (1,1) – первая строка, первый столбец, число 40). Запасы первой базы и первого потребителя одновременно исчерпаны, следовательно, следующая базисная переменная соответствует клетке либо (2,1), либо (1,2) и равна нулю. Пусть базисной будет переменная х 12=0. На базе Б2 находится 60 единиц груза; выделим 40 единиц груза потребителю П2 и оставшиеся 20 единиц потребителю П3. Недостающие 30 – 20 = 10 единиц груза выделим П3 с базы Б3. На базе Б3 осталось 60 – 10 = 50 единиц груза; выделим их потребителю П4 (принцип распределения: сначала распределяем все, что имеется на данной базе и лишь затем переходим к следующей).
Составили первый план. Проверим, является ли этот план допустимым (все заявки должны быть удовлетворены, все запасы исчерпаны), то есть суммы поставок по строкам должны быть равны запасам на базах, а по столбцам – запросам потребителей. Проверим, является ли полученный план опорным. Количество базисных переменных, а, следовательно, заполненных клеток должно быть m + n –1= 3+4–1=6. IV. Проверим план на оптимальность, то есть будет ли при этом плане общая сумма денежных затрат на перевозку минимальной, или ее можно еще уменьшить путем изменения плана перевозок. Для исследования полученного плана на оптимальность используют метод, называемый «методом потенциалов». Он состоит из двух этапов: 1. К таблице добавляют строку и столбец, в которых записывают числа (потенциалы) по строкам U i и по столбцам V j. Эти числа подбирают так, чтобы для занятых клеток выполнялось равенство: U i + V j + Cij=0. (2.11) 2. Вычисляют «оценки» перевозок в клетках по формуле: C/ ij =U i +V j +C ij, (2.12) где C |



 .
. .
. стремится к максимуму.
стремится к максимуму.

 . Суммирование проводится по всем базисным переменным. Иными словами коэффициенты, стоящие в первом столбце таблицы умножаются на элементы j-ого столбца матрицы, произведения суммируются, и из результата вычитается коэффициент целевой функции при хj.
. Суммирование проводится по всем базисным переменным. Иными словами коэффициенты, стоящие в первом столбце таблицы умножаются на элементы j-ого столбца матрицы, произведения суммируются, и из результата вычитается коэффициент целевой функции при хj. . (2.8)
. (2.8) .
.





 .
. .
. .
. . Затем получившуюся строку умножим на –
. Затем получившуюся строку умножим на – 


 , если
, если

 Þ
Þ  и
и  .
. .
. .
.
 Þ
Þ 
 ;
;  ,
, .
. .
. . Проверим его на оптимальность.
. Проверим его на оптимальность. .
.
 Þ
Þ 


 .
. (2.9)
(2.9) (2.10)
(2.10)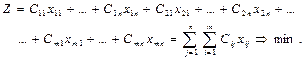

 .
.


