
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наблюдаемость в линейных системах управленияСодержание книги
Поиск на нашем сайте
Для линейной стационарной управляемой системы нами установлено, что существует управление, которое переводит систему из любого состояния На практике, как правило, все компоненты вектора состояний не доступны для измерения (например, потому, что часть переменных состояний в принципе нельзя измерить). Обычно выходными величинами объекта служат лишь отдельные компоненты вектора состояний, либо линейные комбинации этих компонент. В связи с этим в теории управления рассматриваются так называемые задачи о наблюдаемости, основным содержанием которых является установление алгоритмов определения части или всех координат системы при условии, что известна другая часть координат или некоторые функции от этих координат, а также математическая модель системы управления в виде системы дифференциальных уравнений. Для оценки состояния естественно воспользоваться информацией о выходных величинах системы и о ее структуре, т.е. о матрицах
Определение. Задачу нахождения вектора
где Рассмотрим матрицу
Наблюдаемость стационарной системы (2.11) связанасо свойствами матрицы Теорема 2.3. (критерий наблюдаемости стационарной системы). Линейная стационарная п-мерная система (2.11) вполне наблюдаема тогда и только тогда, когда ранг матрицы Доказательство критерия наблюдаемости аналогично доказательству теоремы 2.2. Замечание. В случае, если вектор
МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ В теории вариационного исчисления разработан универсальный математический аппарат, позволяющий решать экстремальные задачи в функциональных пространствах. Этот аппарат позволяет решать широкий круг оптимизационных задач, в том числе и задачи оптимального управления. Постановка задачи оптимального управления как Задачи вариационного исчисления Задачей вариационного исчисления является задача отыскания функций, доставляющих экстремальное (максимальное или минимальное) значение некоторым величинам, которые зависят от этих функций и называются функционалами. Функционал можно рассматривать как функцию особого рода, в которой роль независимой переменной играет другая функция. Рассмотрим постановку задачи оптимального управления и основные задачи вариационного исчисления (Лагранжа, Майера, Больца). Задача оптимизации системы управления Дано: – дифференциальные уравнения системы управления
где – начальное состояние системы
– критерий оптимальности
Требуется определить вектор-функцию Задача Лагранжа Дано: – функционал – – начальные условия
Требуется найти вектор-функцию Предположим, что система уравнений (3.1) позволяет найти управление
Подставляя вектор
Таким образом, задача оптимизации системы управления заключается в нахождении оптимальной траектории системы из условия минимума функционала (3.7), что полностью совпадает с задачей Лагранжа. Как известно, основными задачами вариационного исчисления, кроме задачи Лагранжа, являются задача Майера и задача Больца. Напомним их постановку в терминах и символах теории систем управления. Задача Майера. Дано: – уравнения движения системы (3.1); – начальное состояние системы(3.2); – конечное состояние системы
– критерий оптимальности
где Требуется определить вектор-функцию Замечание 1. В этой задаче условия (3.8) могут заменяться условиями
Замечание 2. Если в задаче Майера функция Задача Больца Дано: – уравнения движения системы (3.1); – начальное состояние системы (3.2); – конечное состояние системы (3.8) или (3.8*); – критерий оптимальности
где Задача заключается в нахождении функции Формулировка задачи Больца - наиболее общая. Но всегда возможно ввести некоторые дополнительные переменные, преобразующие задачу Лагранжа в задачу Больца или в задачу Майера и наоборот. На наш взгляд, целесообразно рассмотреть один такой прием, достаточно часто используемый в приложениях. Рассмотрим задачу Лагранжа (3.1), (3.2), (3.3). Введем дополнительную переменную
или, иначе
Присоединяя уравнение (3.12) ксистеме (3.1), а условие (3.13) к начальным условиям (3.2), получим
Итак, задача оптимизации управления сведена к нахождению экстремума критерия
при условиях (3.14) и (3.15), т. е. к задаче Майера. Приведем теперь основные положения вариационного исчисления, используемые для оптимизации систем управления.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.251 (0.006 с.) |

 в заданное
в заданное  за произвольное время. Можно произвольно менять состояние замкнутой системы в том случае, если все компоненты вектора состояния доступны для измерения.
за произвольное время. Можно произвольно менять состояние замкнутой системы в том случае, если все компоненты вектора состояния доступны для измерения. и
и 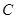 системы уравнений (1.1):
системы уравнений (1.1): (2.11)
(2.11) состояния системы (2.11) или отдельных его компонент по известной на некотором промежутке
состояния системы (2.11) или отдельных его компонент по известной на некотором промежутке  функции
функции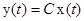 , (2.12)
, (2.12) матрица, будем называть задачей наблюдаемости линейной системы (2.11). При этом вектор
матрица, будем называть задачей наблюдаемости линейной системы (2.11). При этом вектор  называют функцией выхода системы (2.11).
называют функцией выхода системы (2.11). размером
размером 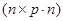 , первые
, первые 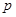 столбцов которой совпадают со столбцами матрицы
столбцов которой совпадают со столбцами матрицы  , следующие
, следующие  и т. д., последние
и т. д., последние 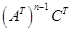 . Матрицу
. Матрицу 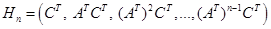 . (2.13)
. (2.13) .
. имеет вид столбца
имеет вид столбца 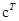 , а поэтому необходимое и достаточное условие полной наблюдаемости принимает форму
, а поэтому необходимое и достаточное условие полной наблюдаемости принимает форму . (2.14)
. (2.14)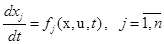 ; (3.1)
; (3.1) и
и  – векторы размерности n;
– векторы размерности n; ; (3.2)
; (3.2) . (3.3)
. (3.3)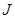 и удовлетворяющую условиям (3.1), (3.2).
и удовлетворяющую условиям (3.1), (3.2).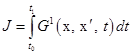 ; (3.4)
; (3.4)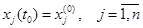 . (3.5)
. (3.5) . (3.6)
. (3.6)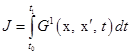 . (3.7)
. (3.7)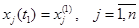 ; (3.8)
; (3.8) , (3.9)
, (3.9) функция, определенная на не полностью заданном множестве конечных состояний системы.
функция, определенная на не полностью заданном множестве конечных состояний системы.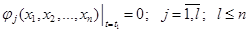 . (3.8*)
. (3.8*) , то она становится задачей о быстродействии.
, то она становится задачей о быстродействии. , (3.10)
, (3.10) и
и  по формуле
по формуле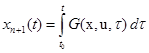 , (3.11)
, (3.11)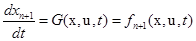 , (3.12)
, (3.12) . (3.13)
. (3.13) , (3.14)
, (3.14)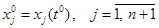 . (3.15)
. (3.15) (3.16)
(3.16)


