
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейных многомерных систем управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Итак, уравнения движения линейной многомерной стационарной непрерывной системы в матричной форме имеют вид
где размерности соответствующих векторов и матриц были определены в (1.1). При исследовании многомерных систем широко используют понятие функции от матрицы, в частности, понятие матричной экспоненты Определение. Функцией
Лемма 1.1. Пусть Доказательство этой леммы можно найти в [4, с.58]. Определение. Матрица
тогда и только тогда, когда в ее столбцах стоят Определитель любой фундаментальной матрицы называется определителем Вронского. Определитель Вронского не обращается в нуль ни в одной точке интервала Теорема 1.1. Если матрица
будет матрица
(здесь Доказательство. Процесс доказательства этой теоремы осуществляется непосредственной подстановкой матрицы (1.16) в уравнение (1.15) с учетом единственности решения и возможности ее дифференцирования. Теорема 1.2. Если матрица
является вектор
Доказательство осуществляется непосредственной проверкой. Теорема 1.3. Если матрица
имеет вид
Доказательство этой теоремы осуществляется непосредственной проверкой. Формула (1.18) является формулой Коши для системы (1.17). Для определения временных характеристик систем управления важную роль игает функция
Положим в равенстве (1.18) все компоненты вектора
где Матрица, столбцами которой являются векторы Импульсная переходная матрица имеет вид
Сопоставляя матрицу
Таким образом, импульсную переходную матрицу можно представить в виде ряда экспоненты
С другой стороны, поскольку определитель фундаментальной матрицы
Непосредственно из определения вытекают следующие свойства импульсной переходной матрицы: 1. 2. 3.
Заметим, что импульсная переходная матрица – это такая фундаментальная матрица, которая удовлетворяет начальному условию Пример 1.3. Рассмотрим уравнение простого осциллятора
Обозначая
где Импульсная переходная матрица для этой системы удовлетворяет уравнению
при начальном условии Ряд (1.19) для вычисления
Простое вычисление показывает, что
где использованы разложения тригонометрических функций в ряд Тейлора
Следовательно,
Пример 1.4. Рассмотрим неоднородное дифференциальное уравнение
которое можно представить в виде нормальной системы уравнений
Вычисление переходной матрицы немедленно дает
Используя формулу Коши
получим общее решение системы
Заметим, что несмотря на внешнюю простоту выражения для переходной матрицы в стационарной системе, вычисление функции С помощью импульсной переходной матрицы
Определение. Пусть
или, что то же самое,
Здесь преобразование по Лапласу матрицы понимается как матрица преобразований по Лапласу всех ее элементов. Применяя преобразование Лапласа к равенству (1.20) и учитывая теорему о свертке (произведение изображений)
для (1.22) можем получить соотношение
где
Для решения обыкновенных дифференциальных уравнений широко используется аппарат преобразования Лапласа. Этот аппарат можно непосредственно использовать для вычисления импульсной переходной матрицы следующим образом. Используем принятое обозначение для преобразования Лапласа функции
где Рассмотрим стационарную однородную систему
и ее преобразование Лапласа
Тогда
Матрица
Последовательность вычислений такова: 1. Вычисление обратной матрицы 2. С помощью таблиц обратного преобразования Лапласа (см. Приложение) определение элементов переходной матрицы
Пример 1.5. Пусть система Характеристическая матрица: Вычисляем обратную матрицу. При этом определитель исходной матрицы:
Пользуясь таблицей обратного преобразования Лапласа (см. Приложение), получим
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

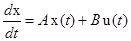 , (1.13)
, (1.13)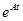 , где
, где  – матрица.
– матрица.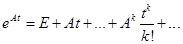 (1.14)
(1.14) ,элементы которой равны действительным или комплексным числам. Тогда ряд (1.14) сходится абсолютно для всех конечных
,элементы которой равны действительным или комплексным числам. Тогда ряд (1.14) сходится абсолютно для всех конечных 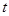 и равномерно на произвольном конечном промежутке.
и равномерно на произвольном конечном промежутке.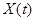 размером
размером  называется фундаментальной (или интегральной) матрицей системы
называется фундаментальной (или интегральной) матрицей системы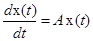
 и, следовательно, фунда-ментальная матрица при любом значении
и, следовательно, фунда-ментальная матрица при любом значении 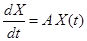 ,
, 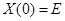 (1.15 )
(1.15 )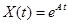 (1.16 )
(1.16 )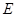 – единичная матрица порядка
– единичная матрица порядка 
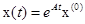 .
. ,
, 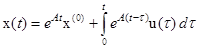 . (1.18)
. (1.18)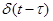 , представляющая собой обычную
, представляющая собой обычную 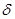 –функцию Дирака, обладающую свойствами:
–функцию Дирака, обладающую свойствами: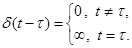
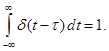
 равными нулю, за исключением одной
равными нулю, за исключением одной 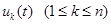 , которую примем равной единичному импульсу
, которую примем равной единичному импульсу 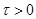 . Обозначим через
. Обозначим через  решение (1.18) уравнения (1.17) при условии
решение (1.18) уравнения (1.17) при условии 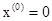 . Тогда будем иметь
. Тогда будем иметь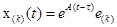 ,
, – единичный вектор-столбец с 1 в
– единичный вектор-столбец с 1 в  -ой строке.
-ой строке.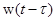 .
.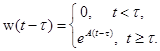
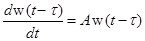 ,
, 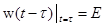 .
. (1.19)
(1.19)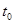 существует обратная матрица
существует обратная матрица 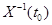 . Тогда для произвольной фундаментальной матрицы
. Тогда для произвольной фундаментальной матрицы 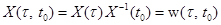 . (1.20)
. (1.20)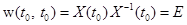 .
.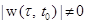 при всех
при всех 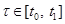 .
. . Действительно,
. Действительно,
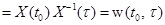 .
. .
. .
.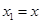 и
и 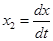 , получим нормальную форму уравнения движения системы в матричном виде:
, получим нормальную форму уравнения движения системы в матричном виде: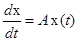 ,
,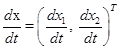 ,
, 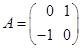 ,
, 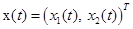 .
.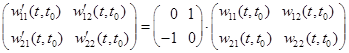
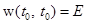 .
.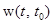 в этом примере легко суммируется потому, что матрица
в этом примере легко суммируется потому, что матрица 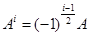 для
для 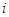 нечетных и
нечетных и 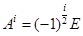 для
для 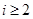 четных. Например,
четных. Например,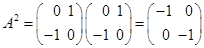 ,
,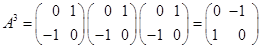 ,
,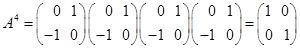 и т.д.
и т.д.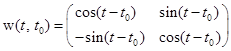 ,
,
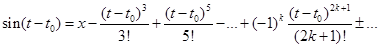
 ,
,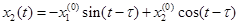 .
. ,
, .
. .
.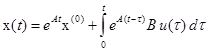
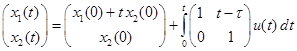 .
.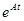 может оказаться сложной задачей.
может оказаться сложной задачей.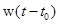 можно записать удобную связь между выходными и входными сигналами системы управления (1.13) при условии, что последняя находится в покое до момента подачи входного сигнала. Эта связь устанавливается в соответствии с результатом теоремы 1.3 и имеет вид
можно записать удобную связь между выходными и входными сигналами системы управления (1.13) при условии, что последняя находится в покое до момента подачи входного сигнала. Эта связь устанавливается в соответствии с результатом теоремы 1.3 и имеет вид . (1.22)
. (1.22)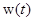 импульсная переходная матрица некоторой системы управления. Если существует преобразование Лапласа матрицы
импульсная переходная матрица некоторой системы управления. Если существует преобразование Лапласа матрицы 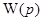 , т. е.
, т. е.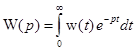 , (1.23)
, (1.23)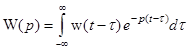 . (1.24)
. (1.24)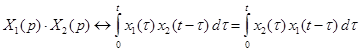 ,
,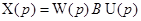 ,
,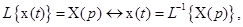
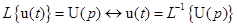 .
. :
: 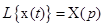 . Тогда, согласно теории этого преобразования, если функция
. Тогда, согласно теории этого преобразования, если функция  ,
,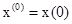 .
.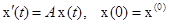
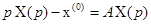 .
.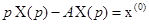 или
или 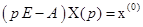 .
.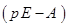 является характеристической матрицей матрицы
является характеристической матрицей матрицы 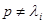 где
где 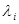 – характеристические числа матрицы
– характеристические числа матрицы 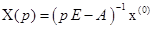 имеет смысл при всех
имеет смысл при всех 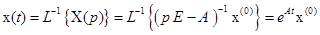 .
.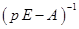 .
.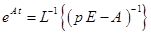 .
.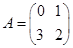 . Построить импульсную переходную матрицу.
. Построить импульсную переходную матрицу.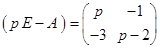 .
.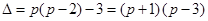 . После несложных преобразований обратная матрица будет иметь следующий вид:
. После несложных преобразований обратная матрица будет иметь следующий вид: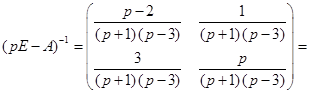
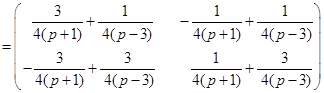 .
.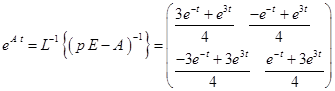 .
.


