
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 4. Принцип максимума Понтрягина.Содержание книги
Поиск на нашем сайте Система управления описывается следующим дифференциальным уравнением:
где Требуется определить управление Построить фазовые траектории системы управления.
Вариант 7 Задача 1. Построение импульсной переходной матрицы системы. Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.
Задача 2. Управляемость и наблюдаемость системы. Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:
где Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния Задача 3. Построение оптимального управления методами классического вариационного исчисления. Линейная система управления описывается следующим дифференциальным уравнением:
где Требуется определить оптимальный процесс перевода системы из одной точки фазового пространства
в другую заданную точку фазового пространства
за фиксированный отрезок времени
управляющего сигнала
Задача 4. Принцип максимума Понтрягина. Система управления описывается следующим дифференциальным уравнением:
где Требуется определить управление Построить фазовые траектории системы управления.
Вариант 8 Задача 1. Построение импульсной переходной матрицы системы. Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.
Задача 2. Управляемость и наблюдаемость системы. Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:
где Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния Задача 3. Построение оптимального управления методами классического вариационного исчисления. Линейная система управления описывается следующим дифференциальным уравнением:
где Требуется определить оптимальный процесс перевода системы из одной точки фазового пространства
в другую заданную точку фазового пространства
за фиксированный отрезок времени
управляющего сигнала Задача 4. Принцип максимума Понтрягина. Система управления описывается следующим дифференциальным уравнением:
где Требуется определить управление Построить фазовые траектории системы управления.
Вариант 9 Задача 1. Построение импульсной переходной матрицы системы. Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:
Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа. Задача 2. Управляемость и наблюдаемость системы. Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:
где Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 , (1)
, (1) ;
;  .
. , обеспечивающее быстрейший перевод системы (1) из состояния
, обеспечивающее быстрейший перевод системы (1) из состояния 
 вначало координат
вначало координат  при условии, что на управление должно удовлетворять ограничению
при условии, что на управление должно удовлетворять ограничению  .
.

 ;
;  ;
;  .
. в состояние
в состояние  .
. ,
, ;
;  .
.

 , затрачивая при этом минимум энергии
, затрачивая при этом минимум энергии
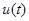 .
. ;
;  .
. .
.
 ;
;  ;
;  .
. ;
;  .
.

 ;
; 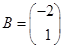 .
.
 ;
;  .
.


